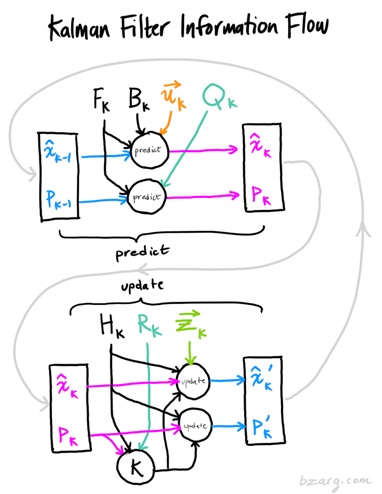
首先分成两个Part吧:
直观和
公式。
预备知识
1. 协方差矩阵是对称矩阵,对角线上是各维度本身的方差,其他是不同维度间的协方差;
2. 贝叶斯公式: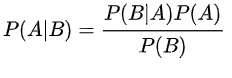 3. 多维高斯分布:
3. 多维高斯分布: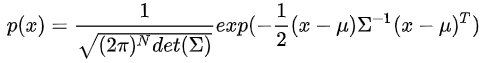 4. 期望和协方差矩阵: 在
4. 期望和协方差矩阵: 在![[公式]](https://www.zhihu.com/equation?tex=x%5Csim+N%28%5Cmu%2C%5CSigma%29) 时,
时,![[公式]](https://www.zhihu.com/equation?tex=E%5By%5D%3DE%5BAx%2Bb%5D%3DA%5Cmu%2Bb)
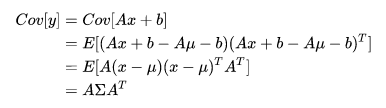
直观部分
先来说一说
直观的。借鉴了这篇的图文:https://courses.engr.illinois.edu/ece420/sp2017/UnderstandingKalmanFilter.pdf
对一个小车的状态进行估计,假设无外力作用,即保持初速度持续不断的运动。假设
马尔科夫性,即
![[公式]](https://www.zhihu.com/equation?tex=x%28t%29)
只与
![[公式]](https://www.zhihu.com/equation?tex=x%28t-1%29)
有关,给出一个递推方程
![[公式]](https://www.zhihu.com/equation?tex=x%28t%29%3DAx%28t-1%29)
。理论上可以通过这个方程求出任意时刻的状态,但是事实上会受到
不确定因素的影响。
我们假设每个状态分量受到的不确定因素(噪声)服从正态分布,那么小车的状态分量也就服从正态分布,现在对小车进行状态估计。
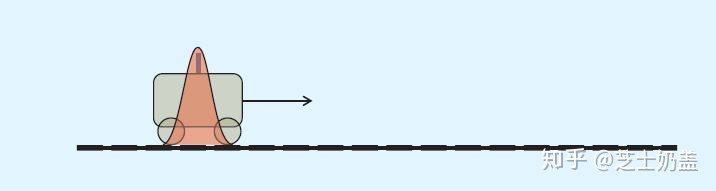
上图是t=0时小车的位置服从的状态分布。

通过公式预测出小车在t=1时刻位置的正态分布(如上图)。
因为加了噪声,所以不确定度增加了,分布也变宽了。这时为了避免不确定度带来的偏差,用传感器测量一次小车的位置,如下图深色分布:

当然,传感器测量同样有不确定因素的干扰,这时,你该相信哪个呢?传感器也可能出错,估计方程也有偏差,这里就需要加权,卡尔曼滤波的K,也就是卡尔曼增益就是这个权重。这里捎带着提一下
![[公式]](https://www.zhihu.com/equation?tex=K%3D%5Chat%7BP_k%7DC_k%5ETQ%5E%7B-1%7D)
后面会在公式部分进行推导,这里的
![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7BP_k%7D)
就是方程推算是一个后验概率,
![[公式]](https://www.zhihu.com/equation?tex=C_k%5ET)
和
![[公式]](https://www.zhihu.com/equation?tex=Q%5E%7B-1%7D)
都是传感器观测方程的参数。

加权后的结果就是图中绿色部分了。
公式推导部分
这里我使用的是视觉SLAM十四讲中的最大后验概率推导,可能比书上看的明朗些,因为高博喜欢不写中间过程或者不给出之前从哪得到过的结论,直接拿来用。
声明:
![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx_k%7D)
是后验概率,
![[公式]](https://www.zhihu.com/equation?tex=%5Cbreve%7Bx_k%7D)
是先验概率
状态估计和观测模型的方程:①
![[公式]](https://www.zhihu.com/equation?tex=%5Cbegin%7Bcases%7D++++++++x_k%3DA_kx_%7Bk-1%7D%2Bu_k%2Bw_k%26%2Cw_k%5Csim+N%280%2CR%29%5C%5C+++++++++z_k%3DC_kx_k%2Bv_k%26%2Cv_k%5Csim+N%280%2CQ%29+%5Cend%7Bcases%7D)
可以看出是线性方程。
![[公式]](https://www.zhihu.com/equation?tex=%5Cbreve%7Bx_k%7D)
先验与
![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx_%7Bk-1%7D%7D)
的方程:②
![[公式]](https://www.zhihu.com/equation?tex=%5Cbegin%7Bcases%7D+%5Cbreve%7Bx_k%7D%3DA_k%5Chat%7Bx_%7Bk-1%7D%7D%2Bu_k%5C%5C+%5Cbreve%7BP_k%7D%3DA_k%5Chat%7BP_%7Bk-1%7D%7DA_k%5ET%2BR+%5Cend%7Bcases%7D)
,
![[公式]](https://www.zhihu.com/equation?tex=w_k)
的均值是0,故不加在
![[公式]](https://www.zhihu.com/equation?tex=%5Cbreve%7Bx_k%7D)
上了。
要求算的方程: ![[公式]](https://www.zhihu.com/equation?tex=P%28%5Chat%7Bx_k%7D%7C%5Chat%7Bx_%7Bk-1%7D%7D%2Cu_k%29%3DP%28z_k%7C%5Cbreve%7Bx_k%7D%29P%28%5Cbreve%7Bx_k%7D%7C%5Chat%7Bx_%7Bk-1%7D%7D%2Cu_k%29)
意义:后验是由先验信息 ![[公式]](https://www.zhihu.com/equation?tex=%5Cbreve%7Bx_k%7D) 和其他信息
和其他信息 ![[公式]](https://www.zhihu.com/equation?tex=z_k) 综合得出的
综合得出的
等式右侧都符合高斯分布,为啥子?因为噪声都是高斯分布的且是以0为均值,加上估计值当然是以估计值为均值的高斯分布了。
那么我们可以这样写:③
![[公式]](https://www.zhihu.com/equation?tex=N%28%5Chat%7Bx_k%7D%2C%5Chat%7BP_k%7D%29%3DN%28C_kx_k%2CQ%29N%28%5Cbreve%7Bx_k%7D%2C%5Cbreve%7BP_k%7D%29)
,在②式中给出了
![[公式]](https://www.zhihu.com/equation?tex=N%28%5Cbreve%7Bx_k%7D%2C%5Cbreve%7BP_k%7D%29)
的均值、协方差矩阵的求法。
随后我们对③式中高斯分布的
二次项进行计算:
高斯分布公式:(看到exp后面的了吧)
![[公式]](https://www.zhihu.com/equation?tex=p%28x%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B%282%CF%80%29%5ENdet%28%5CSigma%29%7D%7Dexp%28-%5Cfrac%7B1%7D%7B2%7D%28x-%5Cmu%29%5CSigma%5E%7B-1%7D%28x-%5Cmu%29%5ET%29)
推导:
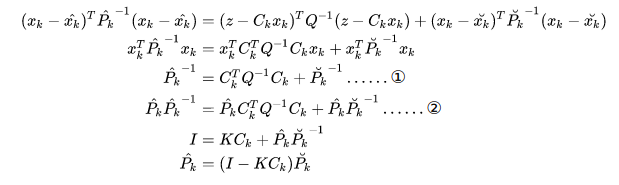 ①这个式子后面我们会用到!
①这个式子后面我们会用到!
②步将
![[公式]](https://www.zhihu.com/equation?tex=K%3D%5Chat%7BP_k%7DC_k%5ETQ%5E%7B-1%7D)
这就是
卡尔曼增益。
这样就有了
![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7BP_k%7D%3D%28I-KC_k%29%5Cbreve%7BP_k%7D)
,可以注意到这里的卡尔曼增益是用了
![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7BP_k%7D)
算出来的,感觉有点转圈圈,就是要求的东西放到求解的式子里了好像没有移项。
这里我们使用刚才推导给出的①式对
![[公式]](https://www.zhihu.com/equation?tex=K)
继续推:
就有了:
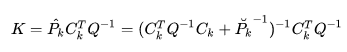
根据SMW(Sherman-Morrison-Woodbury)恒等式:
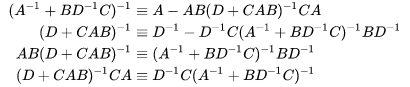
上述的最后一个恒等式,可得:
![[公式]](https://www.zhihu.com/equation?tex=K%3D%5Cbreve%7BP_k%7DC_k%5ET%EF%BC%88C_k%5Cbreve%7BP_k%7DC_k%5ET%2BQ_k%29%5E%7B-1%7D)
。
好了现在要求的后验概率已经求出了协方差,还有均值要求解,对③式中高斯分布的
一次项进行计算:
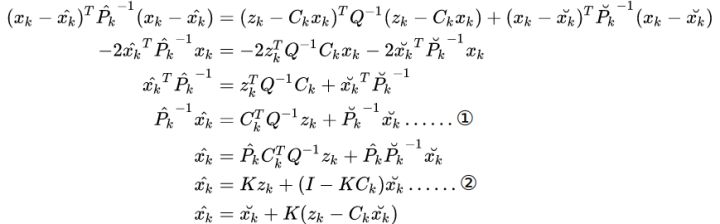
其中式①是将等号左右均求转置,由于协方差矩阵是对称矩阵,所以不变。式②使用了
![[公式]](https://www.zhihu.com/equation?tex=K%3D%5Chat%7BP_k%7DC_k%5ETQ%5E%7B-1%7D)
和
![[公式]](https://www.zhihu.com/equation?tex=I%3DKC_k%2B%5Chat%7BP_k%7D%5Cbreve%7BP_k%7D%5E%7B-1%7D)
。最终得到了
![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx_k%7D%3D%5Cbreve%7Bx_k%7D%2BK%28z_k-C_k%5Cbreve%7Bx_k%7D%29)
即如何递归的求解均值。
到这里公式部分就结束了。
 首先分成两个Part吧:直观和公式。
首先分成两个Part吧:直观和公式。
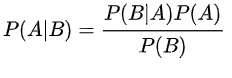 3. 多维高斯分布:
3. 多维高斯分布: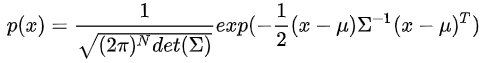 4. 期望和协方差矩阵: 在
4. 期望和协方差矩阵: 在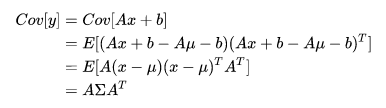
 上图是t=0时小车的位置服从的状态分布。
上图是t=0时小车的位置服从的状态分布。
 通过公式预测出小车在t=1时刻位置的正态分布(如上图)。
因为加了噪声,所以不确定度增加了,分布也变宽了。这时为了避免不确定度带来的偏差,用传感器测量一次小车的位置,如下图深色分布:
通过公式预测出小车在t=1时刻位置的正态分布(如上图)。
因为加了噪声,所以不确定度增加了,分布也变宽了。这时为了避免不确定度带来的偏差,用传感器测量一次小车的位置,如下图深色分布:
 当然,传感器测量同样有不确定因素的干扰,这时,你该相信哪个呢?传感器也可能出错,估计方程也有偏差,这里就需要加权,卡尔曼滤波的K,也就是卡尔曼增益就是这个权重。这里捎带着提一下
当然,传感器测量同样有不确定因素的干扰,这时,你该相信哪个呢?传感器也可能出错,估计方程也有偏差,这里就需要加权,卡尔曼滤波的K,也就是卡尔曼增益就是这个权重。这里捎带着提一下  加权后的结果就是图中绿色部分了。
加权后的结果就是图中绿色部分了。
和其他信息
综合得出的
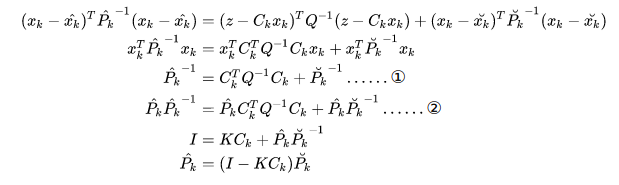 ①这个式子后面我们会用到!
②步将
①这个式子后面我们会用到!
②步将 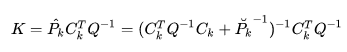
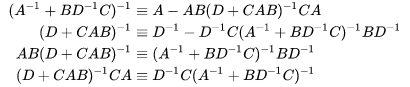
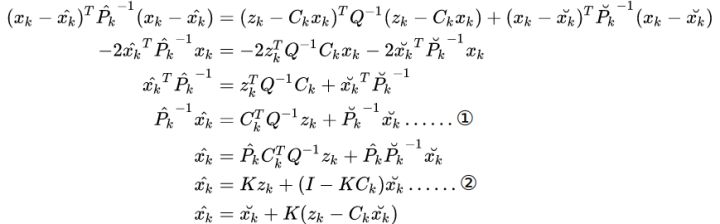 其中式①是将等号左右均求转置,由于协方差矩阵是对称矩阵,所以不变。式②使用了
其中式①是将等号左右均求转置,由于协方差矩阵是对称矩阵,所以不变。式②使用了 




评论(0)
您还未登录,请登录后发表或查看评论