在最优化中，目标函数和约束函数皆为线性函数的优化问题称为线性规划（LP），它是相对简单的最优化问题。

标准形式

• 线性规划：

  如下形式的线性规划记2-1：

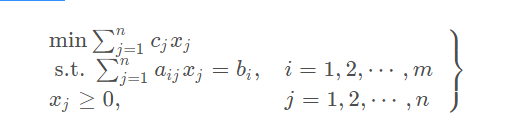
称为线性规划的标准形式。其中c j 
​    
 称为价格系数，b i 
​    
 称为右端项。

  采用向量－矩阵表示法，标准形式可以简写为如下形式，记为2-2:

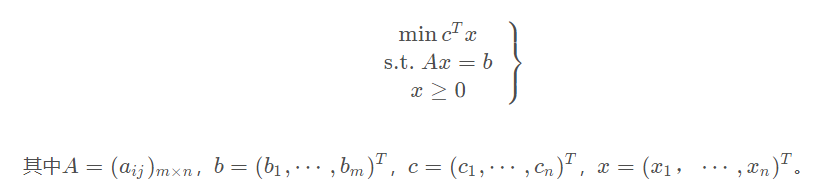
典范形式：
  在下面进行理论分析时，经常把A 看作由n 个列向量构成的，即：

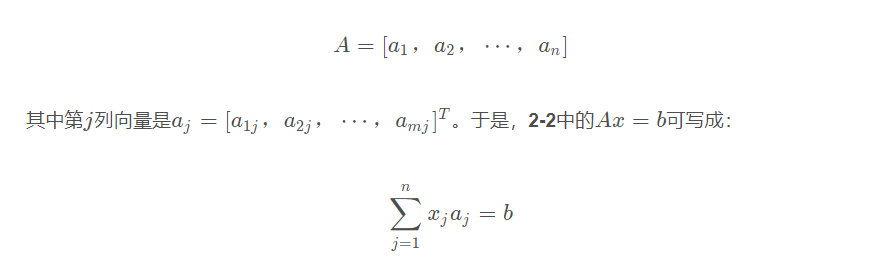
一般形式化标准形

  对于一般形式的线性规划，比如标准形式中是求极小，而有时候给出的是求极大，所以我们需要将其化成标准形，然后对标准形做研究，得到通用的解法。

  那么实际问题中出现的非标准形式如何处理呢？有三个基本原则：

• (1) 极大化极小：

(2) 松弛变量和剩余变量：
  如约束中出现≤ \leq≤，则在该约束中加上一个变量（称为松弛变量），并要求该变量非负；如出现≥ \geq≥，则在该约束中减去一个变量（称为剩余变量）。
注意：新引入变量的价格系数全部设为零，因此目标函数中没有出现新变量。

(3) 自由变量：
  以上讨论都考虑变量的取值是非负的。实际中，如果某些变量没有这种约束，也就是说，某些变量可以任意取值，那么这些变量称为自由变量。自由变量可以通过以下两种方法把它消除。
第一种方法：引入两个非负变量x 1 + x和x 1 − x令x 1 = x 1 + − x 1 将其代入到线性规划的目标函数和约束函数中，自由变量 x 1 
​    
 就消除了。注意，求出新线性规划的最优点后，再利用x 1 = x 1 + − x 1 − x
 便可以定出x 1 
第二种方法：取一个包含x 1 x
​    
 的等式约束，例如a i 1 x 1 + a i 2 x 2 + ⋯ + a i m x n = b i 
​    
 由此解出：

第一种方法将增加变量的数目，导致问题的维数增大。第二种方法正好相反。

解的性质
  在介绍解的性质之前，先需要了解一下各种各样的解的概念。

  满足A x = b 的x 称为方程组A x = b Ax=bAx=b的解，而满足A x = b x ≥ 0 0的x 称为线性规划2-2的容许解。现在要定义一种特殊的容许解-基本容许解，而在介绍基本容许解之前需要介绍另一个概念：基。

定义：A 的m 个线性无关列向量称为基。基中的每个列向量称为基向量，而A 中的其余列向量称为非基向量。由全体基向量合成的矩阵称为基矩阵，也简称为基。若基是单位矩阵，则称为标准基。

定义： 在约束∑ j = 1 n x j a j = b 
 =b中，确定一个基后，与基向量对应的变量称为基变量，与非基向量对应的变量称为非基变量。

定义： 设x 0 是A x = b的一个解。若它有m 个分量所对应的A 的列向量构成基B ，而其余n − m 个分量全部为0，则x 0 
​    
 称为约束A x = b 关于基B 的基本解。若x 0 
​ 还满足x 0 ≥ 0 则x 0  称为约束A x = b，x ≥ 0 关于基B 的基本容许解，也称为线性规划2-2关于基B 的基本容许解。

简单地说，在确定基之后，所有非基变量取值都为0的解是基本解，所有非基变量取值都为0的容许解是基本容许解。

定义：设B 是2-2的一个基。若2-2存在关于B 的基本容许解，则称B是2-2的容许基；否者称为非容许基。若容许基是单位矩阵，则称为标准容许基。

  上述所涉及到的概念，总结如下，方便复习：

解
容许解
基
基向量
非基向量
基矩阵
标准基
基变量
非基变量
基本解
基本容许解
容许基
非容许基
标准容许基
定义： 若基本解中基变量的取值都不为0，则该解称为非退化的；否者称为退化的。若2-2的所有基本容许解都是非退化的，则线性规划2-2称为非退化的；否者称为退化的。

  若线性规划是非退化的，则容许基与其基本容许解是一一对应的。相反地，退化地基本容许解可能与多个容许基相对应，也就是说不同的容许基会有相同的容许解。

基本容许解与极点地对应关系
  约束：