一、概述

在目前主流的融合框架里，基本就分为优化和滤波两大类，滤波我们在前面通过大量的篇幅已经介绍过了，这里就介绍基于优化的方法。

优化的方法仍然是一个包含复杂内容的东西，一篇文章肯定也介绍不完，所以我们在本篇文章里，同样只介绍基础知识部分，基于优化的融合放在下一篇文章介绍。

二、优化问题定义

为了避免后续内容陷入繁杂的公式推导中摸不着方向，所以我们得先搞清楚优化是在做什么，也就是先定义什么是优化问题。

我们之前多次提过，融合就是使用多种传感器得到一个最优的位姿结果，这里面其实分三步，第一步是把传感器的模型建立出来，第二部是综合多种传感器建立一个总的目标（残差），第三步是以目标为导向（让残差降到最小），寻找对应的最好位姿。实际上，这里的优化问题，其实做的就是第三步。

把上面定义的问题，用数学语言重新描述一下，就是

找到n维的变量  ，使得损失函数  取局部最小值，即

方程中，  是残差函数，在实际使用中，它可以代表任何方式得到的残差，比如 ICP 中点到点之间的距离、融合中预测与观测之间的误差等等。这代表着，我们已经可以脱离具体的模型来讨论这个问题，也就是说，无论用的什么样的传感器，传感器的模型具体是什么样，都可以用这样的通用模型来表示它的优化问题，后面的讨论同样满足这个条件。

三、优化方法思路

所有的优化方法，其实都可以解释为“反复迭代去逼近最优值”，后面会介绍多种优化方法，但他们都不会脱离这样的迭代套路：

1) 给定某个初值 

2) 对于第k次迭代，寻找增量  ，使得  达到极小值

3) 若足够小，则停止

4) 否则，令  ，返回第2步

我们可以看出，其实只要给出增量的形式，剩下的步骤就完全是一样的。因此，后面在介绍方法时，我们的推导只截止到给出增量为止，不再重复写出这4个步骤了。

四、优化方法介绍

常见的优化方法有下面这样几种

1.最速下降法

损失函数可以泰勒展开如下

其中  和  分别为损失函数  对变量  的一阶导(也叫梯度或Jacobian矩阵)和二阶导(也叫Hessian矩阵) 。

最速下降法只保留一阶泰勒展开结果，取增量为

即沿梯度的反方向取增量，则可以保证使损失函数减小。

剩下的就按照迭代方法的那4步固定套路去走就可以了。

从上面的推导我们可以看出，最速下降法具有迭代方便、计算简单等优点，但是，一阶近似毕竟精度有限，所以在迭代时容易走出锯齿形状（如下图），而且越接近目标值，步长越小，前进越慢。

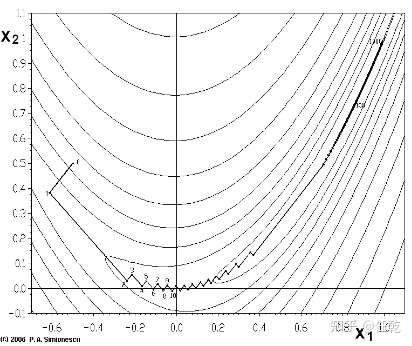
2.牛顿法

牛顿法保留二阶泰勒展开结果，此时的增量方程为

求右侧等式关于 Δx 的导数，并令它为零

上式移项可得

求解该方程，即可得到所需的增量。剩下的同样按4步套路走。

从原理上可以看出，对原函数的近似更精确，每一步的收敛更加准确，且收敛速度快，但它有一个明显的缺点，即需要计算 H 矩阵，在优化规模较大时，不容易做到。

3.高斯牛顿法

高斯牛顿法是为了解决牛顿法的缺点而诞生的。它对 f(x) 进行泰勒展开，而非 F(x)

此时优化问题变成了，寻找增量 Δx ，使得

 达到最小，即

同样的，需要对右侧求导，并令导数为零。右侧展开为

求导并令导数为零

即

最终的求解的增量为

可以看出，高斯牛顿法用

  做为牛顿法中 H 的近似，从而避免了直接求解二阶导数矩阵。但这样也带来一些缺点，求解增量就必须保证 H 矩阵是可逆的，而

只能保证半正定，此时算法稳定性变差，最终导致不收敛。

4.LM方法

LM方法推导起来略显复杂，这里就直接给出增量方程的结论啦（如下），详细的细节可以参考《视觉slam十四讲》第6.2节。

该方法好处是可一定程度避免 H 不正定带来的病态问题。实际使用中，当问题性质较好时，用高斯牛顿法；问题接近病态时，用LM方法。

五、总结

不加一节总结就觉得缺点啥，但又没啥可写。。。