1. 李群和流形
首先,要明白李群和李代数是一种数学抽象概念,如同集合等概念一样,而并不就是机器人位姿这样具体的概念。而能够代表机器人位姿的SE(3)或SO(3)等就是具体的李群元素,如同自然数、负数等集合的具象化一样。
而某个李群G,定义为一个光滑的流形(manifold),由一个集合G和定义在该集合上的一个操作 组成,具体的定义就不再赘述了。
而流形可以理解为一个光滑、曲面和非线性的高维空间。而光滑这个定义就说明了对于流形上的每个点,都有一个唯一的切平面(tangent space)。这个切平面与李代数相关,而且是一个向量空间,这就为后续我们做微分铺平了道路。
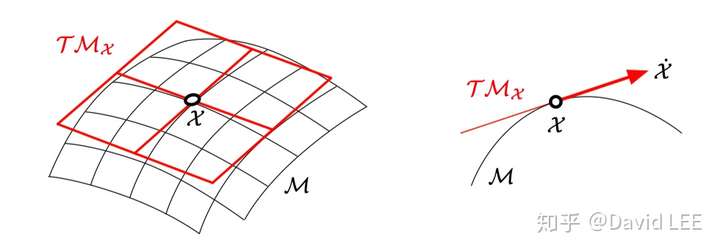
对一个李群而言,该李群所在的流形在每一点上都一样。对应地,任意点上的切空间也就都类似了。而群的定义(及其数学操作上的性质),使得对于该流形上的元素进行操作后的结果仍然落在这个流形上。根据定义,群中的一个特殊元素即为幺元。对应地,幺元对应的切空间也是比较特殊的,该向量空间就是这个李群所对应的李代数。
1.2 李群的操作与举例
李群具有“变换“其他集合中的元素的能力,如机器人学中讨论的SO(n), SE(n)和相似变换群Sim(n)。利用数学语言来表示,假设有李群M和一个集合V,用 来表示这种转换能力(注意与李群自身的操作
区分),即有
这样的能力也是其应用在状态估计领域的基础。
而这样的变换满足结合律:
对于常见的几个李群,这样的操作具体为
1.2.1 举例
单位负数 是一个最简单的李群
。其幺元为1,逆即为该负数的共轭,群上的操作为乘法。
其所对应的操作为与一个向量 相乘,表示将这个向量旋转
角,得到另一个向量
。
对应的流形即为一个定义在负平面上的单位圆。从下图也可以看出,它的李代数为对应的负数轴 。而指数映射就是熟悉的欧拉公式
,对数映射即为
。而从图中也可以看出,指数/对数映射是一个满射。
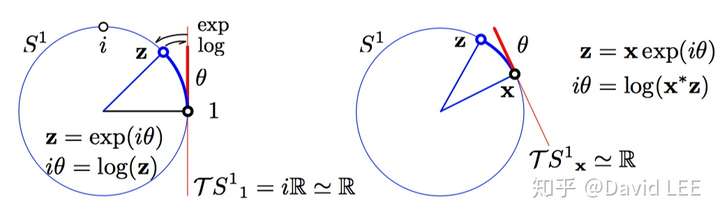
可以注意到,除了幺元的切空间(李代数) 外,李群中的其他元素也有切平面
,两者之间是存在一个转换关系的。
2. 切空间,李代数和向量空间
2.1 从切空间到李代数
前面提到,流形上的每一点都存在切空间,而且他们也都是类似的。但特殊的一个是幺元处的切空间,它是这个李群所对应的李代数。这是为什么呢?我们做个直观的解释。
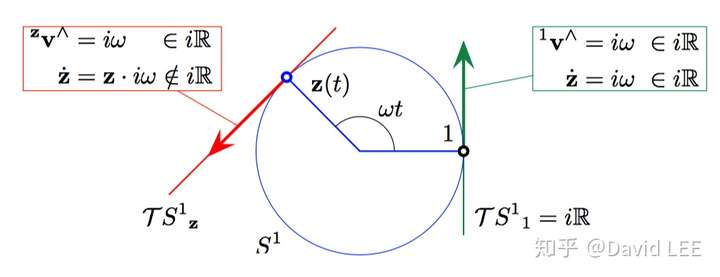
用单位负数这个李群来说明。假设其上有一个点z按照恒定角速度 在旋转,该点可以表示为
,它经过了两个点:幺元1还有点z。
当它经过点z的时候,其速度(某个点的速度在对应点的切空间上,因此也是该点切空间的表示) 在全局坐标系 (global frame) 下可以表示为
;但在其切空间的局部坐标系 (local frame) 下,其速度表示为
。二者间的关系为
.
但在幺元处,二者的表示是统一的: 。由上一小节的举例中我们也可以知道,
的切空间的结构都为iR,这也是
的李代数的结构。这和幺元处的速度
的结构是相同的,也说明了幺元处的切空间即为对应李群的李代数。
2.2 李代数
将李群的幺元表示为 ,把切空间表示为
,这个李群M对应的李代数m即可表示为
有如下几个性质:
- 李代数m是一个向量空间,其维度与对应的李群的自由度相同;
- 李代数和李群间的转换是通过指数\对数映射完成的;
- 李群中其他元素X的切空间上的向量可以转换到幺元
的切空间上,该转换是个线性变换,称为伴随。
由李代数的定义可以知道,李代数由一个向量空间和一个运算符(李括号)组成,并伴有一些性质。不引入其他符号,李代数m可以表示为 ,其中
为对应的向量,而
则是该向量及其对应的李代数之间的转换。例如对于SO(3),
代表了三个旋转角,而
,
在这里等价于取反对称矩阵的操作。而对应的逆操作为
要注意到A才是李代数,而是李代数所在的向量空间。这点很重要,因为其实我们更加关心的是这个向量空间而不是李代数。只有使用了向量,我们才能进行各种线性代数的操作,或者把好几个向量堆叠成一个矩阵。
此外,对于SO(3)来说, 是对向量取反对称矩阵的操作,但对于其他李群却不是这样的,例如我们熟悉的SE(3)就不是。而对单位负数
而言,
;对于单位四元数而言,
。为了区分,使用
表示对向量t取反对称矩阵。
2.3 指数/对数映射
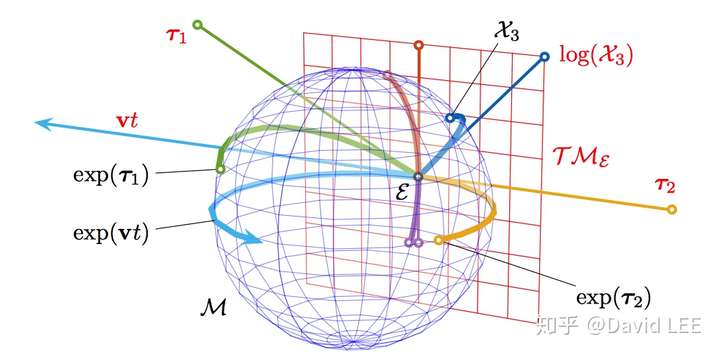
从上图可以直接看到,指数/对数映射是李群和李代数之间的一个精确映射。 下面可以进行一下推导。
对李群的自反性 这个等式对时间求导,就可以得到
。回顾第一节举例中国呢点z(t)经过点z时,两种坐标系下速度的表示关系,就会发现这个式子正好是李代数的表示:
如果李群为SO(3),那么这就是泊松公式。
继续推导,有 。这是个微分方程,解之可得:
由于X(t)和X(0)都是李群中的元素,那么 显然也是李群中的元素。因此,指数映射完成了从李代数到对应李群的映射。
对于指数映射,有如下几个等式:
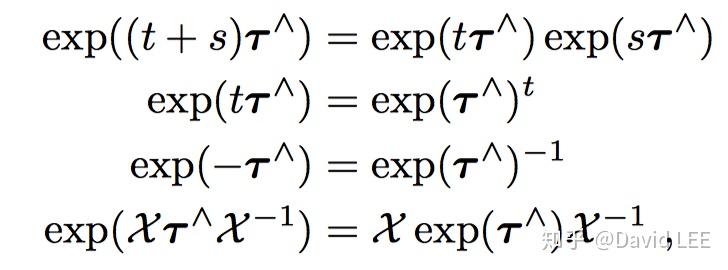
如前所述,其实我们更想在李代数关联的那个向量空间(而不是李代数本身)上进行操作,因此,定义大写的指数/对数映射:
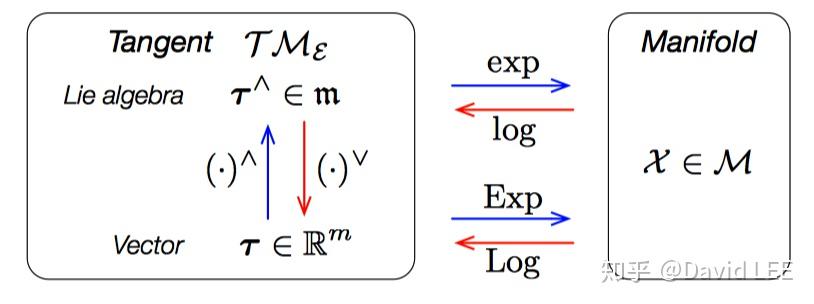
2.4 左右操作符
既然流形上的任意一点都存在切空间,因此,将幺元上的切空间的向量表示为 ,表示的是全局坐标系(global frame);而其他元素的切空间表示为
,表示的是局部坐标系(local frame)。
为了更好地表达流形上的增量,方便后续我们引入微小量进行求导等操作,引入左右加减法。
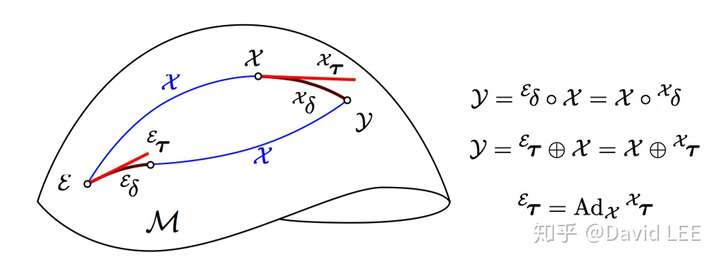
从上图可以看到,这两种表达方式都是一样的,只不过是在不同坐标系下进行操作。
需要注意的是,的结果是落在向量空间的。而
的一个操作数
也是落在向量空间的。明确操作数落在流形还是向量空间对于后面理解和使用左右加减符号是很重要的。
3. 伴随
之前文章中讲到了SE(3)的伴随,但对它的作用没有进行更多地介绍。这里我们再次重温下它,并且会在后面和左右操作符一起经常用到它。
通过上一小节左右加法的两个等式,我们就有 。显然,这是全局坐标系(幺元处的切空间)和局部坐标系(其他元素的切空间)之间的一个转换关系。
于是有
由此,对于李群M上的一个元素X,可以定义它的伴随 :
所以, 表示了全局坐标系和局部坐标系之间的转换。并且,伴随还具有如下两个性质:
3.1 向量空间上的伴随
前面说过,我们更希望在向量空间上操作,为此还定义了Exp/Log映射,考虑到伴随操作也是线性的,因此,我们也定义一个矩阵伴随 ,用于操作和李代数相关联的向量空间:
对于矩阵伴随操作,也有如下性质:
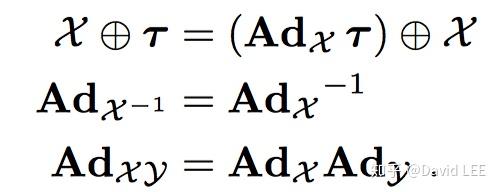
3.2 举例
对于SE(3),我们有
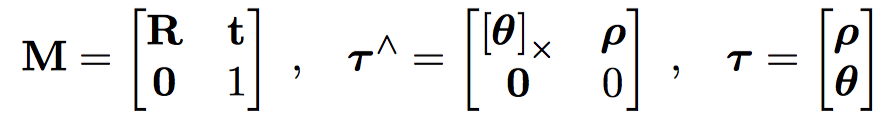
根据伴随的定义,我们有
因此, 。翻看前面的文章,可以发现,这和之前定义的相同。
4. 关于李群的导数
前面已经把整个李群和李代数的框架和概念讲清楚了。对于李群和李代数,我们最关心的是它们的各种导数。因为这涉及到非线性优化时的雅可比矩阵推导。现在,万事俱备,就让我们来看看李群上的各种导数。
4.1 左右雅可比矩阵
通过前面的定义,再配上之前定义的右 操作,很自然就可以计算李群的右雅可比矩阵:
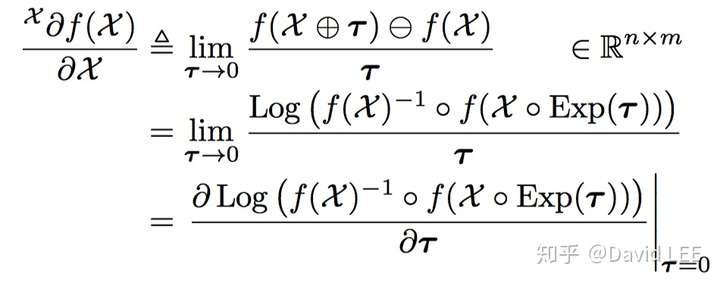
注意到Log操作符,在流形元素 和
上的变化就被映射到了局部坐标系的向量空间上。因此,我们得到的是一个正确的雅可比矩阵
,完成两个切空间之间的线性映射:
。
举例而言,对于SO(3),有方程 来旋转一个空间三维点,代入到上面的公式就有:
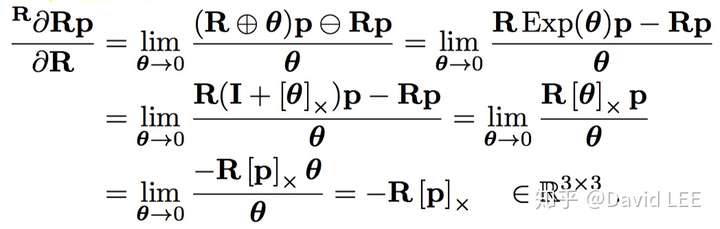
需要注意的是,是在流形M上进行操作的(SO(3));
则是在流形N上进行操作的(
中操作的,因此我们中直接只用了向量空间中的减号)。
同样地,如果我们在全局坐标系之下,使用左 操作,就可以得懂李群的左雅可比矩阵:
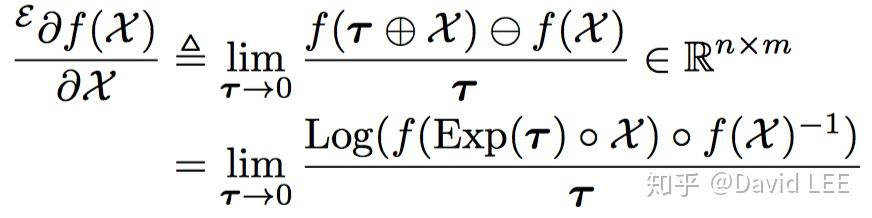
与右雅可比矩阵相比,左雅可比矩阵完成的是两个全局坐标系之间的映射: ,亦即流形M和N的李代数。
最后,左右雅可比矩阵可以通过M和N的伴随联系起来:
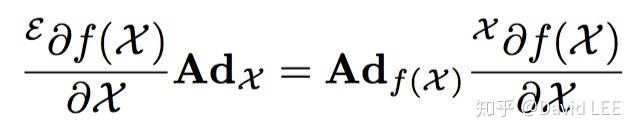
后面,我们默认使用右雅可比矩阵。
这里直观地展示下流形上的雅可比矩阵。
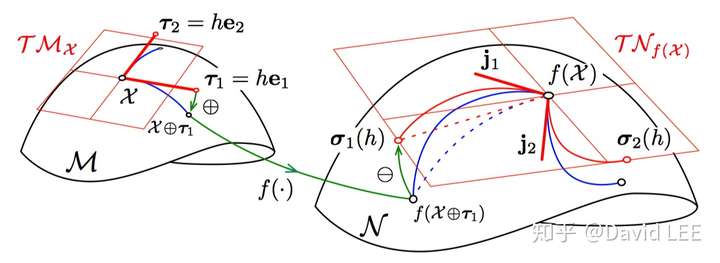
将流形M上的元素X的切平面上的扰动 分解到主方向上,得到
。然后,经过
,f()和
就得到了流形N上的元素f(X)的切平面上的扰动
。
对于流形M来说,切空间上的扰动 (TM上的红色粗直线)经过Exp映射(
是包含了一个Exp映射的),得到流形M上的扰动(M上的蓝色曲线)。而经f映射后,由于f的非线性,得到的流形N上的扰动
(N上的蓝色实线)并不真正落在流形N上(N上的蓝色虚线才是“真的扰动”)。但这个“假”扰动的Log映射结果
(TN上的红色细曲线)和“真”扰动的Log映射结果是一样的。而
的切线j即为方向导数。将之组合起来,就得到了了雅可比矩阵
,完成了
中的向量到
中的向量的映射。
4.1.1 局部坐标系的作用
对于公式 是针对恒定速度v的。假如v是不断变化的,那么我们倾向于将一段时间t分解成更多段时间
,每小段时间内速度都是恒定的。这样一来就可以有:
如下图所示
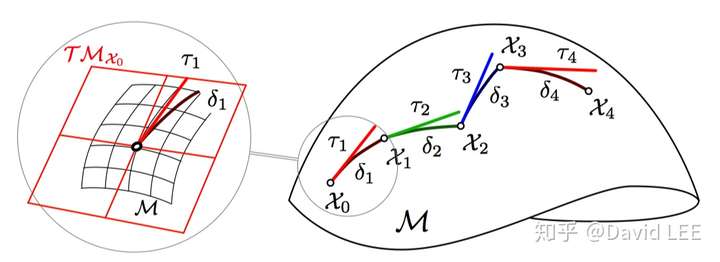
注意到,每一小步 都是落在李群元素
的切空间上,即局部坐标系上,映射在流形上一小步
。因此,我们使用右雅可比矩阵和右操作符:

4.2 更多情况下李群的导数
假设某个函数f(X)是的自变量是一个流形,我们可以研究下各种常见f下李群的导数。
假设Z=g(Y)=g(f(X)), X, Y, Z都是流形。那么针对X上的一个扰动 在不同情况下对Z的影响有:
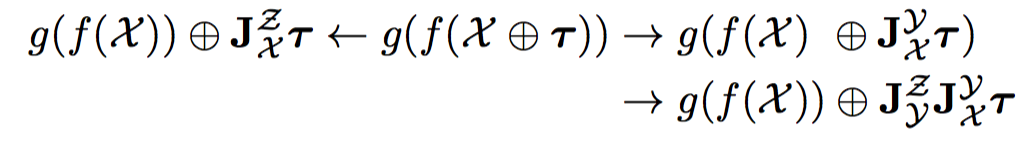
4.2.2 逆
定义 ,根据之前的公式就有:
4.2.3 结合
其中,对于第一个式子的推导如下
4.2.4 李群的雅可比
结合前面几讲,可以定义李群自身的左右雅可比矩阵:
右雅可比矩阵将向量 上的扰动映射到对应的流形的局部坐标系
上;而左雅可比矩阵将向量
上的扰动映射到对应的流形的全局坐标系或李代数上。
针对左右雅可比,有我们熟悉的BCH近似公式:
- 右雅可比:
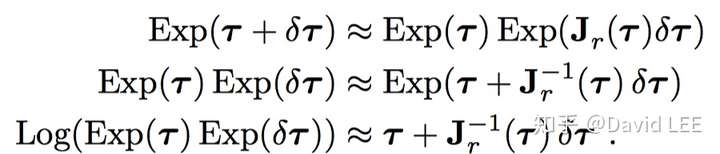
- 左雅可比
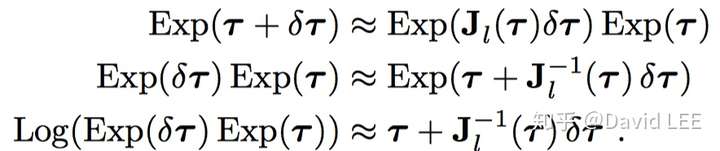
利用上两组公式中 的等价性,我们还可以得到
我们也可以利用链式法则
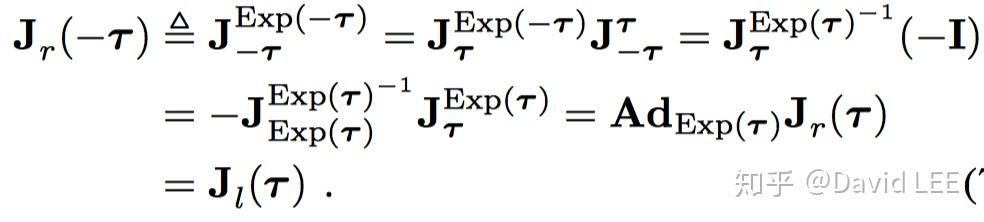
得到左右雅可比之间的关系。
4.2.5 群的操作
对于 和
,我们有
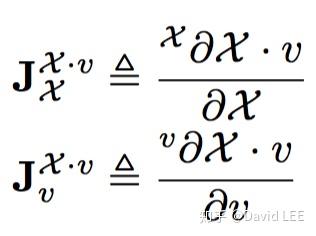
这两个操作涉及到具体的李群,因此在后面的举例中再给出。
4.2.6 Lop映射
对于 , 有
4.2.7 加减操作
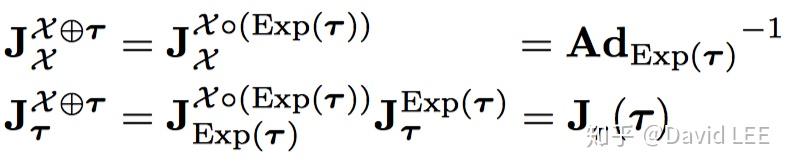
这其实和4.2.3 结合很相似。
而对于 有
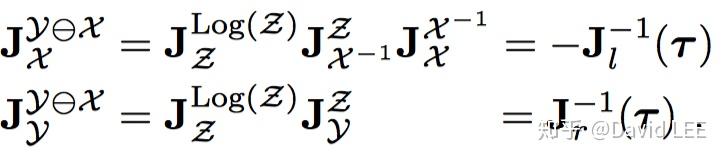
对于第一个式子的推导为
4.3 举例
下面,我们以单位四元数 和SO(3)群为例,来具体看上面这些公式的实例化。
这里,单位四元数为 ,旋转表示为
, u为旋转轴,
为旋转角。
4.3.1 指数/对数映射
对于四元数,有
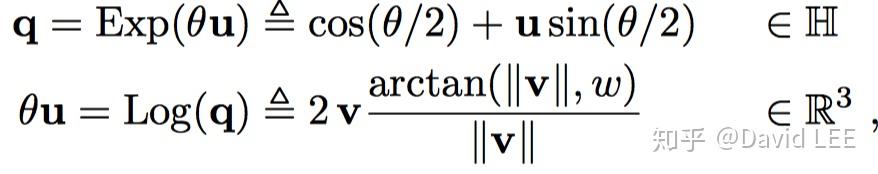
对于旋转矩阵,有
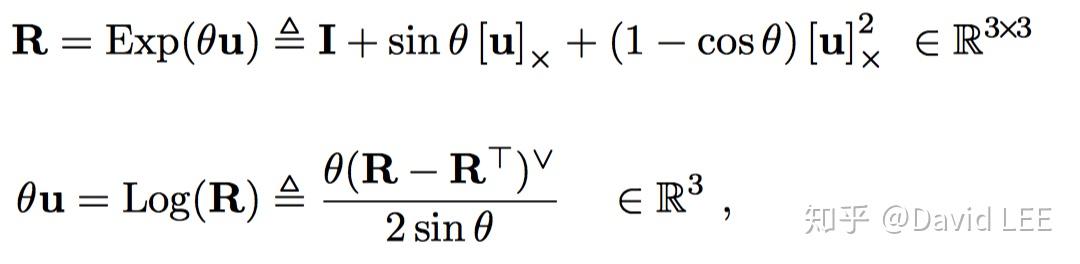
其中,
4.3.2 李群的操作
二者都是用来旋转空间中的三维点。对于单位四元数有
而对于SO(3),有
对于二者之间的联系有
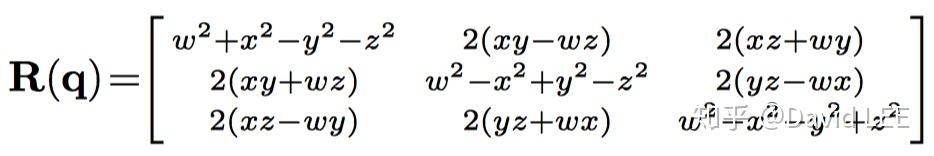
4.3.3 各种导数
对于单位四元数和SO(3)而言,其切向量空间是同质的, ,因此各种导数对二者来说是一样的,所以这里统一说明。
- 伴随
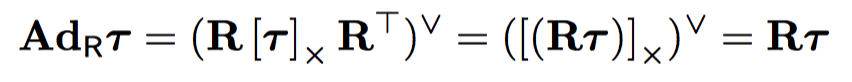
因此有
因此有 .
如果我们还记得这个公式 ,就可以得到
这个公式在[李群和李代数(三):优化基础中讲SO(3)的雅可比矩阵中提到过。是前述通用公式在SO(3)上的实例化。
- 逆与结合
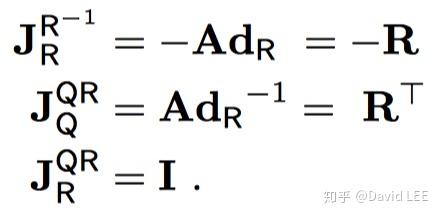
- 左右雅可比矩阵
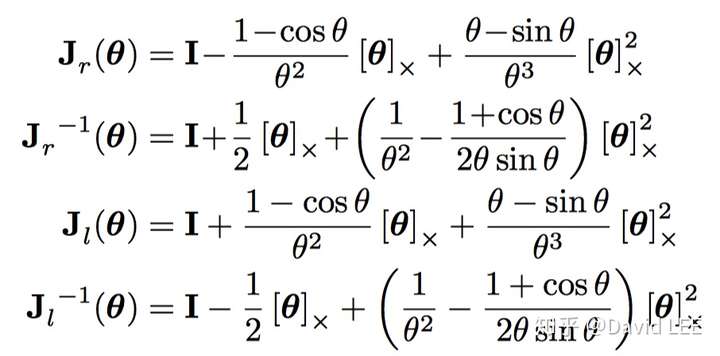
对应的,有
- 右加减操作
假设 ,则有
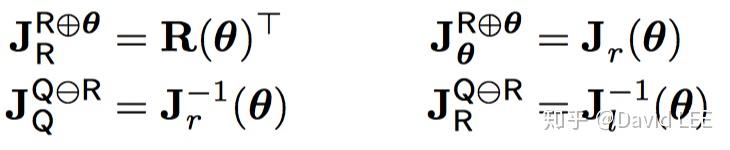
- 群的操作
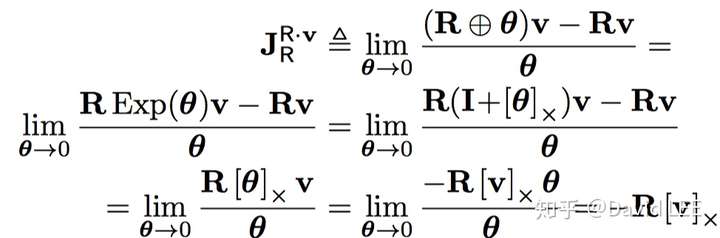
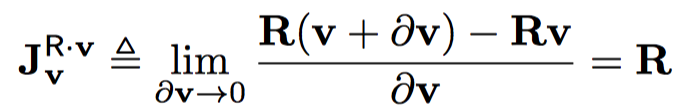
参考文献:
[1] A micro Lie theory for state estimation in robotics.
[2] 《state estimation for robotics》





评论(0)
您还未登录,请登录后发表或查看评论