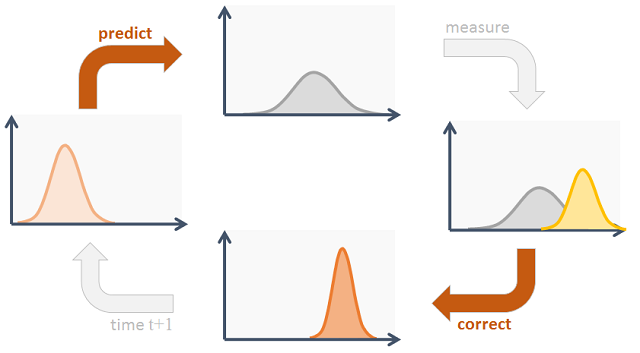
上篇博文简要介绍了卡尔曼滤波器的思想，这篇博文详细推导一下卡尔曼滤波器，确保大家能够看懂所有细节，看完后记得自己推一遍加深印象！

养生的控制人：卡尔曼滤波器（估计器）155 赞同 · 11 评论文章

状态空间方程

假设一个确定性离散时间系统可以用如下状态空间方程描述：

下标代表采样时刻，即  时刻的状态由  时刻的状态和输入决定。

然而真实系统往往没有那么美好，Uncertainty is everywhere！引入过程噪声（或者扰动  ）以及测量噪声  ，则上面状态空间方程表示为

那么我们该如何估计出真实的状态  呢？

数据融合

在每个采样时刻，我们能够得到输出的测量值  ，因此一种对状态的估计就是用测量值（measurement）反算出来（但是肯定不太准）

另一种对状态的估计则是利用上一次的估计结果（calculation）递推（也是不太准）

回顾上一次提到的数据融合的思想（递归思想），对于状态的估计其实就是

即

为了避免求逆，我们可以对上式进一步转化（令  ）

因此卡尔曼滤波器要求的其实就是系数  。

卡尔曼增益推导

从问题出发，我们要估计的是什么？是状态变量，那自然是希望估计值  和真实值  越接近越好！那么我们来衡量一下估计值和真实值之间的差距（  ）：

上式的推导就只是代入状态空间方程后合并同类项。

进一步我们假设这个误差也是个正态分布 

因为我们希望估计值和真实值的误差越小越好，也就是说我们希望误差满足的这个正态分布的方差越小越好，也就转化成了误差的协方差矩阵的迹最小

因此我们需要将协方差矩阵表达式推导出来

代入  ，

把转置放进去

把两个括号的乘积展开成四项，同时引入估计误差 

对每一项进行求期望的操作（因为是线性加减）

注意：常数求期望相当于系数；两个独立变量乘积的期望等于期望的乘积。

因此

同理

所以协方差矩阵剩下两项

将估计误差的协方差矩阵记做  ，上式转化为

展开括号

到现在我们已经推导出协方差矩阵的表达式了，我们要求协方差矩阵的迹最小，这是一个最小化的问题，很直接的做法就是求导令导数为  。即

引入两个个求导的公式

可以得到协方差矩阵的迹的导数为

到这里卡尔曼增益就求出来了！

再回到递推公式

当  特别大的时候，卡尔曼增益趋于零，也就是去相信  ；当  特别小的时候，卡尔曼增益就是  ，即  。再次验证了数据融合的思想。