共轭梯度法是求解稀疏对称正定线性方程组的最流行和最著名的迭代技术之一。

二次函数与最优解

考虑最小化二次函数

其中  且假设矩阵  是对称正定的（SPD）。该函数的最小值  可以根据一阶最优条件得到，即导数为零

或

这也意味着最小化  等价于求解线性方程  。由于二次函数的Hessian矩阵是半正定的，该解具有唯一性。

线搜法

线搜索方法是一类迭代优化方法，其中迭代由下式给出

它的思想是选择一个初始位置  ，然后每一步沿着一个方向走一步使得函数值满足  ，不同的方法在选择搜索方向  和步长  有不同的策略。

最速下降法也许是最直观和最基本的线搜索法。函数的梯度是一个向量，它给出了函数增加最多的方向。最速下降法的策略是：在任何给定点  中，函数  的负梯度给出的搜索方向是最速下降的方向。换句话说，负梯度方向是局部最优的搜索方向。注意对于二次函数而言它的梯度为  ，我们也将它称为系统的残差  。

我们现在有了搜索方向，但是我们仍然需要知道沿着它走多远。很明显，自然的选择是一直走，直到函数值不再下降，最佳步长  的表达式很容易得到（将  带入二次函数后关于  最小化）

重复执行找梯度、找步长直到收敛，可以看到最速下降法的相邻搜索方向是正交的。

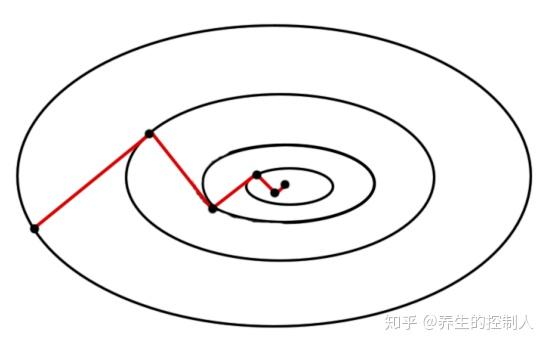
可以看出最速下降法走的路很曲折，这种曲折的路径显然不是最优最快的，我们应该避免这种来回跑的路径！这也就是共轭梯度法要解决的问题。

共轭梯度法

首先介绍一下共轭方向法，一组向量  关于SPD矩阵  是共轭的可以表示为如下的共轭条件：  。这样一组向量是线性独立的因此可以张成整个空间  。进一步我们可以将最优解和初始值的差表示为共轭向量的线性组合

利用共轭性可以得到系数和步长是一致的，即

可以认为这是沿着解空间的维度逐步构建最优解。对于对角矩阵，共轭搜索向量与坐标轴重合。在每一步  中，  将精确解  投影到由  个向量所张成的解空间中。

那么如何寻找共轭方向呢？

1. 根据  的特征向量形成一个  -共轭集，但是寻找特征向量计算量太大了；
2. 第二种选择是修改通常的格拉姆-施密特正交化过程。这也不是最佳的，因为它需要存储所有方向。

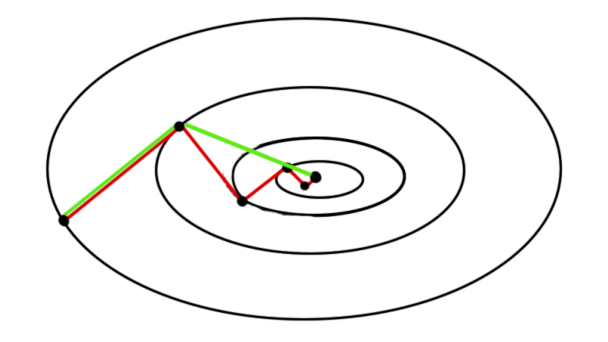
共轭梯度法在寻找每一个共轭向量  时只需要利用上一个共轭向量  ，而不需要记住先前所有共轭向量。每一次迭代用到的新方向是负残差和上一个搜索方向的线性组合。

由于负残差其实就是负梯度方向，这个寻找共轭方向的方法就称作共轭梯度法。其中系数  可以根据共轭条件（  ）得到

红色表示最速下降法，绿色表示共轭梯度法

算法流程

• 计算 
• 每一次迭代  直到收敛

第一步是找出初始残差，其实就是梯度方向。如果初始解  为零，那么  和  简单地变成  。在for循环中，公式（8）为步长的计算。在公式（9）通过往共轭方向走一步来更新解。然后在公式（10）更新残差，公式（11）和（12）计算系数和新的搜索方向。

代码示例

这里分别利用最速下降和共轭梯度法来解一个线性方程

%% linear equation Ax=b
A = [4,-2,-1;-2,4,-2;-1,-2,3];
b = [0;-2;3];

%% 最速下降法
x0 = [0;0;0];
iter_max = 1000;
for i = 1:iter_max
    r = A*x0 - b;
    alpha = (r'*r)/(r'*A*r);
    x = x0 - alpha*r;
    if norm(x-x0)<=10^(-8)
        break
    end
    x0 = x;
end

%% 共轭梯度法
x0 = [0;0;0];
r0 = A*x0 - b;
p0 = -r0;
iter_max = 1000;
for i = 1:iter_max
    alpha = (r0'*r0)/(p0'*A*p0);
    x = x0 + alpha*p0;
    r = r0 + alpha*A*p0;
    beta = (r'*r)/(r0'*r0);
    p = -r + beta*p0;
    if norm(x-x0)<=10^(-8)
        break
    end
    x0 = x;
    r0 = r;
    p0 = p;
end