大部分工程问题到最后都会转化为一个数学问题，控制领域也不例外。经典控制领域，我们费尽心思进行了各种样的变换和计算，最终都是为了得到常微分方程的解。

那为什么常微分方程的解这么重要呢？根本原因是现实中的系统、现象、亦或物理规律，大都可以用常微分方程来描述。系统的表现、现象的变化规律的演化都与方程的解息息相关。

举一个拉弹簧的例子。根据牛二定律，很容易写出作用力F，与物块位移x的关系。它们都是关于时间的t的函数，但我们解出方程的解x(t)时自然就知晓了物块的轨迹。

那么这与控制有什么关系呢？

实际上，在进行拉普拉斯变换前，我们所面对的就是描述系统的偏微分方程。拉普拉斯变换仅仅是为了获取常微分方程解，而采用的一种数学方法。最终的落脚点还是方程的解，我们通过解预测和判断系统的表现。

控制中的稳定指系统在受到扰动后还能回归到平衡点。具体的表现就是：扰动量的系统响应随着时间的增长最后会归零。而扰动量的系统响应就与常微分方程的解联系到一起。

经典控制理论里遇到的常微分方程解有着统一的形式：  ，它表示着扰动响应随时间的变化。而t前面的系数a决定了最终的稳定结果，具体如下：

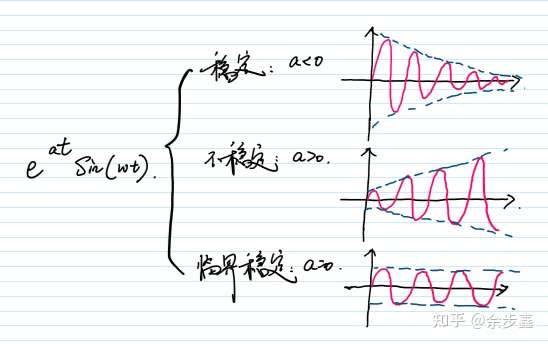
如果a<0，那系统必然稳定，扰动响应最终归于0，并且 a 的绝对值越大，衰减的也越快。因此，a 不仅决定系统的稳定性，还会影响系统的动态响应性能。

综上，控制理论中的一系列操作，稳定性判定，系统矫正等归根结底都是围绕着方程的解展开，因为微分方程才是最终的Boss，它的解才能定乾坤。当然，直接用代数方法求解常微分方程是一件相对困难的事情，所以才有了拉普拉斯变换，才有了特征方程，这一切的一切，都是在帮我们分析“解”啊。

更新，原来写的是“偏微分方程”，概念不对，经知友提醒做了修改，应该是“常微分方程”。具体概念区别可看下面一篇：