一、非线性系统的滤波方法
对于非线性系统，一种常见的解决思路是先进行泰勒级数展开，略去高阶项后近似为线性系统，再做线性Kalman滤波估计。这种处理非线性系统的Kalman滤波方法称为扩展Kalman滤波(EKF)。

1、雅可比矩阵：
在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此，雅可比矩阵类似于多元函数的导数。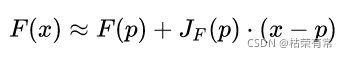

从n维空间映射到m维空间，即状态量为n维，函数个数为m维；则雅可比矩阵为：

雅可比矩阵

2、海森矩阵
黑塞矩阵（Hessian Matrix），又译作海森矩阵、海瑟矩阵、海塞矩阵等，是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。

黑塞矩阵常用于牛顿法解决优化问题，利用黑塞矩阵可判定多元函数的极值问题。
在工程实际问题的优化设计中，所列的目标函数往往很复杂，为了使问题简化，常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数，此时函数在某点泰勒展开式的矩阵形式中会涉及到黑塞矩阵。

海森矩阵

3、EKF滤波

离散时间状态空间模型：

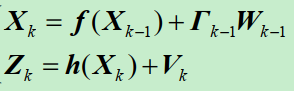
其中：

X_{k}是n维状态向量，;

f(X_{k})是n维非线性向量函数；

Z_{k}是m维量测向量；

h(X_{k})是m维非线性向量函数；

--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--

若已知k-1时刻状态X_{K-1}的一个参考值/初始值(泰勒展开的初始值)记为：X_{k-1}^{n}；

其中，真实值与参考值/初始值的偏差为：

\delta X_{k-1}=X_{k-1}-X_{k-1}^{n}；

<1>通过EKF状态方程对k时刻进行预测，可得：

X_{k/k-1}^{n}=f(X_{k-1}^{n}):

状态预测的偏差为：

\delta X_{k}=X_{k}-X_{k/k-1}^{n}

<2>通过EKF量测方程和状态预测值X_{k/k-1}^{n}对量测进行预测：

Z_{k/k-1}^{n}=h(X_{k/k-1}^{n})

量测预测的偏差为：

\delta Z_{k}=Z_{k}-Z_{k/k-1}^{n}

<3>将偏差量\delta X_{k}和\delta X_{k-1}当作新的状态，且将\delta Z_{k}当作新的量测，则可构成一个新的系统，并且是线性的；

 

则可直接用标准线性kalman滤波方法进行偏差状态估计，公式如下：

 二、随机系统的可观、可控及稳定性和可观测度

1、可控、可观和稳定性

一维线性定常系统：

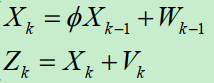
 其中，W_{k}、V_{k}均为零均值白噪声，方差分别为Q\geq 0、R> 0，且两者不想关，根据kalman滤波方程：

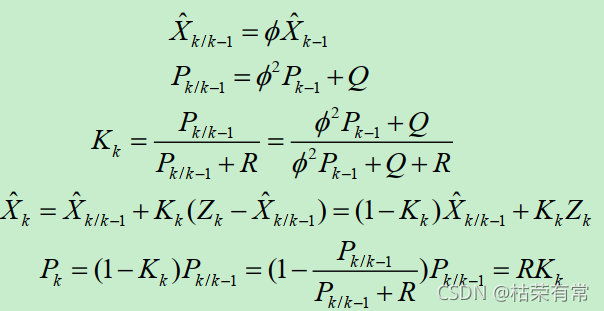
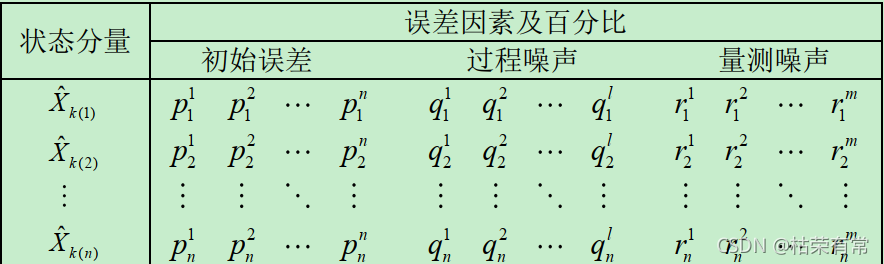
 2、状态估计的误差分配和可观测度分析 

<1>误差分配

当系统模型参数\Phi _{k/k-1}、\Gamma _{k-1}、H_{k}确定后，标准kalman滤波的均方误差阵P_{k}仅与P_{0}、Q_{k}、R_{k}有关，而与状态初值X_{0}及量测Z_{k}无关。

因此，状态估计误差分配问题是：P_{0}、Q_{k}、R_{k}对P_{k}的影响。

kalman滤波均方误差阵的预测及量测更新公式重写如下：

 将上述两式中，第一个式带入第二个式子，可得：

 最终得：

 kalman滤波咋黄台估计的误差分配列表：

 <2>可观测度分析

如果系统建模准确，Kalman滤波均方误差阵P_{k}反映了各状态之间的协方差，其中对角线元素为对应状态分量的估计均方误差。

因此，从P_{k}随时间的变化过程中可以看出状态估计误差的变化情况，对角线元素的变化幅度，正好定量描述了对应状态分量估计效果的强弱程度。

针对状态向量中的每一个分量X_{k(j)} （j=1,2,…，n），定义它的可观测度如下：

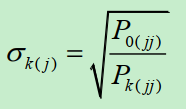
 可观测度是针对某一状态分量在某一时刻而言的，其含义是某一状态分量的0时刻初始设置误差的标准差与同一状态分量在k时刻的滤波误差标准差的比值。

可观测度为无因次数量，在数值上越大，表明在经过Kalman滤波后，相应状态分量的估计误差下降程度越显著，或者说精度提升效果就越明显。

--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--

根据经验，可人为设置如下阈值大致判断状态分量X_{k(j)}的可观测度强弱：

 两种绘制曲线方式：

<1>绘制可观测度\delta _{k(j)}相对于时间k的对数曲线k - log(\sigma _{k(j)})，则能够直观地显示出状态估计地可观测度变化趋势；

<2>绘制出各状态分量误差的标准差曲线k - sqrt(P_{k(jj)})，能够表示出状态估计误差的绝对大小变化情况；

--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--%%--

在实际应用中， 如果针对某一问题， 设计了全面描述系统动力学行为的复杂高维滤波系统，可观测度分析和前述误差分配技术可应用于滤波器的优化：
（1）对于不可观测的状态分量， 宜将其删去， 从而降低系统状态维数，减小滤波计算量；
（2）对于可观测度较弱的状态分量， 与其对应的均方误差阵对角元素的初值不宜设置得太大，否则，对应的均方误差阵设置过大容易引起滤波过程中的估计误差剧烈波动， 在间接滤波中应当慎重使用反馈校正， 反馈时机不当有容易引起滤波发散；
（3）对于可观测度较强的状态分量， 与其对应的均方误差阵对角元素可以设置成较大的初值，即便如此， 在随后滤波过程中也会快速减小收敛；
（4）通过误差分配表，针对可观测的状态分量， 采取恰当措施合理地减小最大误差因素所占的比重，往往能够有效减小相应状态分量的滤波估计误差，即提高滤波估计精度。