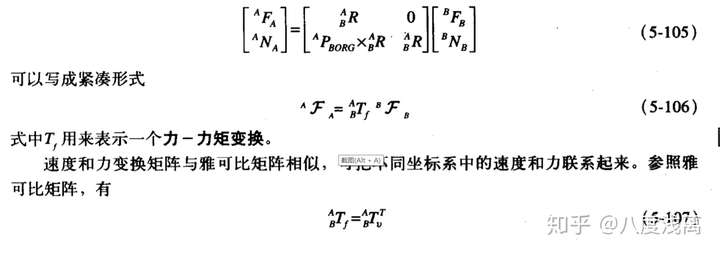
操作臂的静力——求出使末端操作臂支撑住某个静负载所需的一组关节矩。（即已知末端静力求各关节所需的力矩）

力域中的雅可比——将力做功与关节力矩做功联立得出雅可比矩阵的转置将作用在手臂上的笛卡尔力映射成了等效关节力矩的普适结论。即将一个笛卡尔的量转变为一个关节空间的量而无需任何运动学函数的逆解。

速度和静力的笛卡尔坐标变换——把不同坐标系中的速度和力结合起来。

操作臂中的静力

前提：不考虑作用在连杆上的静力。

符号定义：

fi =连杆i-1施加在连杆i上的力；

ni =连杆i-1施加在连杆i上的力矩。

下图是施加在连杆i上的静力和静力矩。

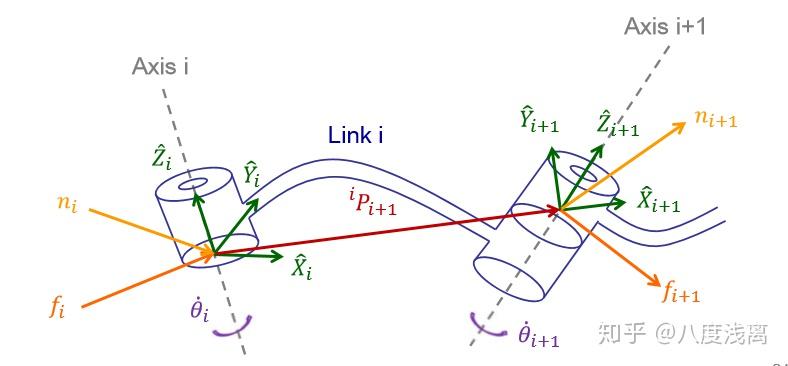
将静力相加并令其为零，有

将绕左边系{i}原点的力矩相加，有

可以看出在操作臂静力中我们是从末端向底座进行迭代的。

写出连杆在自身坐标系下的表达式，有

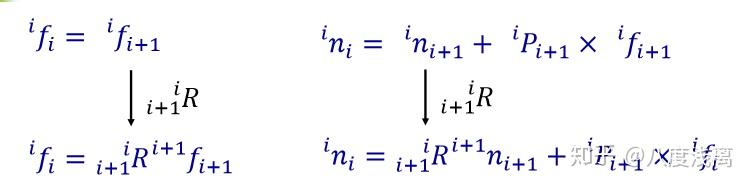
现在已将连杆i所承受静力与静力矩计算出来了，那么什么才是驱动关节需要去承受的呢？将其对关节的旋转轴做投影得出的即为答案。

例子：

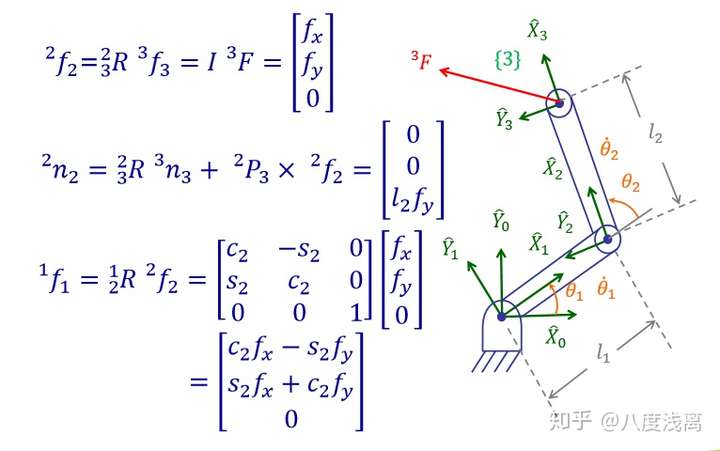
此时，我们会发现矩阵 Τ 是雅可比矩阵的转置，为什么呢？

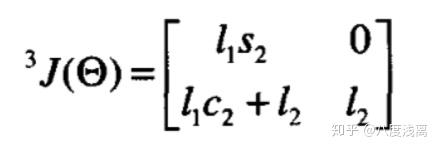
力域中的雅可比

在静态下，关节力矩与在手部上的力平衡。如令位移趋于无穷小就可以用虚功的原理来描述静止的情况。力在笛卡尔空间做的功应该等于力矩在关节空间做的功。在多维空间中，功是一个力或力矩矢量与唯一矢量的点积，有

这就解释了上面例子的答案，同时得出结论：雅可比矩阵的转置将作用在手臂上的笛卡尔力映射成了等效关节力矩。

当得到相对于坐标系{0}的雅可比矩阵后，对坐标系在{0}中的力矢量进行变换：

注意到：式（5-97）将一个笛卡尔的量转变为一个关节空间的量而无需任何运动学函数的逆解。

速度和静力的笛卡尔变换

6✖1维的广义速度与广义力，

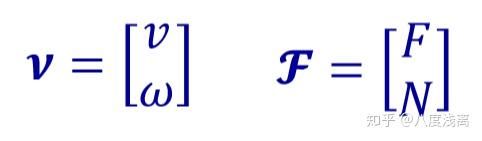
在前面左边变换中有，

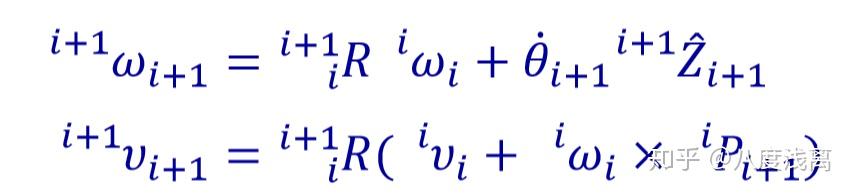
将在坐标系{A}中的广义速度矢量变换为在坐标系{B}的描述。这里涉及的两个坐标系之间是刚性连接的，随意上边出现的 θi+1 一阶导置0，有

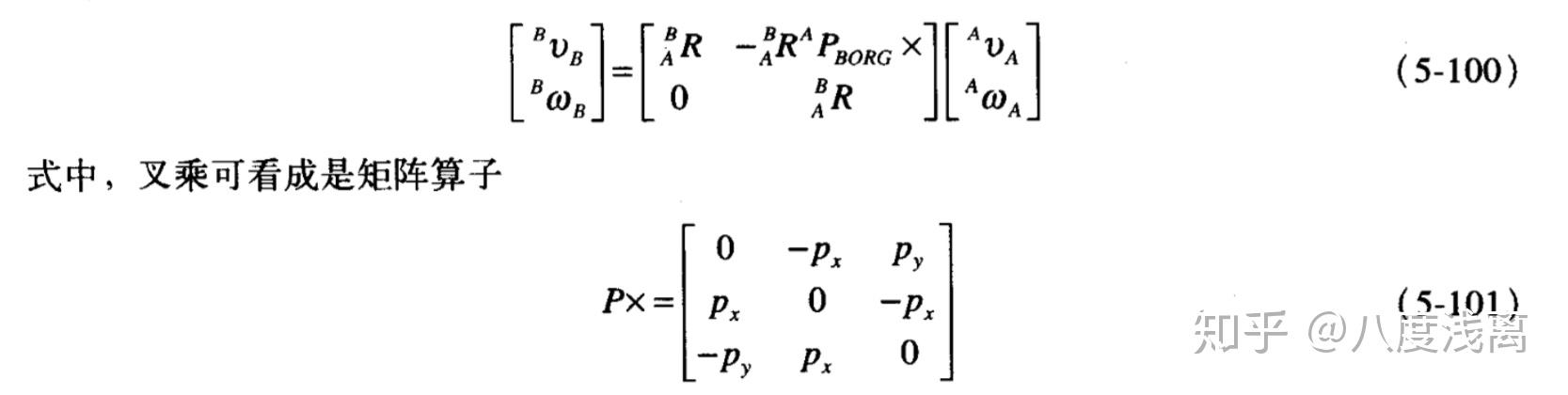
它将一个坐标的速度与另一个坐标的速度相联系，故称其为速度变换矩阵，用符号 Tv 表示。

故（5-100）表示

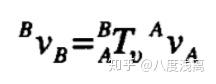
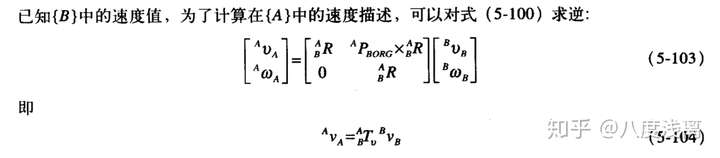
同样，