雅可比矩阵是一个矢量的每一个元素对另一个矢量的每一个元素进行偏微分而组成的矩阵。

可以用来对两个矢量之间的非线性关系进行局部线性化。

机器人学中，雅可比矩阵指的则是机器人末端(end-effector)的位姿（位置与姿态）与机器人各个关节位置值的偏微分关系。

同样， 雅克比矩阵可建立关节运动与手运动之间的联系：

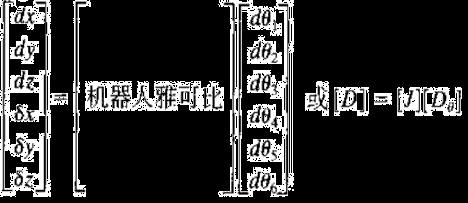
雅克比矩阵的逆

从机器人关节上的微分运动 （或速度） ，得到手的微分运动（或速度），需要计算雅克比矩阵的逆

－－－

知道雅克比矩阵的逆：可计算出每个关节需要以多快速度移动，　才能使机器人手产生所期望的微分运动　或　达到期望的速度

 

微分运动分析的主要目的

目的是分析　而非　进行正向微分运动计算。

例如：

机器人喷胶任务，机器人需要：

１.　沿着特定路径运动

２.　恒定速度

 

＝＝》方法：

  1. 将路径分为小段，期间不断计算关节值以保证机器人沿着预期的路径运动
  2. 确保手保持期望速度， 期间需不断计算关节速度

==》 困难在于：

雅克比矩阵在期间未变， 但数值发生变化；

为能在每秒内计算出足够多的精确关节速度， 需要保证计算过程的高效和快速；

雅克比矩阵的作用

通过读取各关节速度值，计算出末端（end-effector）在笛卡尔空间下的速度值，关节位置对 t求导后，即表示为各个关节的速度值，结合当前构型下的雅克比矩阵，可计算出end-effector在笛卡尔空间下的速度值。

数值化求运动学逆解

机器人的正逆运动学：

正运动学：已知机器人的各个关节位置值Θ已知，有关节位置值导出末端位姿，用函数F表示：x = F(Θ)

逆运动学：给定机器人末端位姿，求解对应关节位置值，在通过电机控制到达相应位姿，可表示为：Θ = F-（x）

问题在于：

函数F(Θ)通常是一个非线性函数，不存在自身的逆函数。

雅克比矩阵作用就显现了：

雅可比矩阵具有和导数类似的性质。因此可以在局部通过导数对一个非线性关系进行线性化。

在任一点对原本的非线性函数求导，可以得到一个线性函数。在局部区域内，使用导函数对原函数的变化量进行逼近：δy ≈ k δx

迭代进行计算的，可以提高求解的精度。这也就是机器人逆运动学数值解的计算方法。