讲完了李群和李代数，就轮到最小二乘优化了。和之前一样，应该会是一系列文章。这一章就先讲讲一些基本的概念和常见的最小二乘算法。

1.问题的定义

一个最小二乘问题的定义如下：

寻找一个关于下列函数的局部最小值  ：

这里，  是误差方程。

而局部最小值的定义为：

给定  ，找到一个  ，使得

这里，  是一个给定的小正数。

假设损失函数F是光滑、可微的，就可以对其进行泰勒展开:

其中，g是一阶导数（gradient）：

而H为海塞矩阵（Hessian）

显然，如果  是一个局部最小值且  足够小，那么我们不可能再找到一个更小的  。

如此，可以先给出一个局部极小值的必要条件：

如果  是一个局部极小值，那么  。

我们知道，满足上述条件的点包括：局部极小值，局部极大值和鞍点，统称为驻点（stationary point）。为了判断一个驻点  是否是一个局部极小值，将之反代回F的泰勒展开式：

由海塞矩阵的定义可知，H是一个对称矩阵。如果它同时是一个正定矩阵的话，那么其特征值会大于某个数值  ，并且

显然，此时  。

由此，可以得到一个局部最小值的充分条件:

假定  是一个驻点，且  是一个正定矩阵，那么  是一个局部极小值。

显然，如果H是一个负定矩阵，那么x是一个局部极大值；如果H既有正的特征值，又有负的特征值，那么s就是个鞍点。

2. 迭代梯度下降方法

对于非线性优化方法，其解法基本都是迭代方法：给定一个起始点  ，不断迭代产生新的  ，并最终收敛至  。为此，引入下降条件（decending condition）：

回到F的泰勒展开式，我们有

 

可以看到，如果  ，那么h就是F的一个下降方向。

很显然，基本所有下降方法都可以概括为以下两步：

1. 找到一个下降方向  ，然后

2. 找到一个迭代步长使得F的值减小；

其中，这个步长  可以通过线性搜索（line search）的方式得到。

2.1 最速下降法

由前面的等式可以得到

该方程表示的是方程F的相对下降（relative gain）。可以发现， 它在 的时候可以获得最大的下降。

由此，可以得到最速下降法的下降方向

最速下降法的特点是在刚开始的阶段有较好的表现，但是到了最后是线性收敛。

对此，也诞生了混合方法（hybrid methods）：在开始阶段使用一种方法，在最后阶段使用另一种方法。

2.2 牛顿法

我们知道，对于局部极小值有  。这是一个非线性方程组，为此，对其进行泰勒展开有：

令上式等于0就可以得到牛顿法：

下次迭代就有

如果H是正定的（说明上式具有唯一解），即对于所有  有  ，则有

说明  是损失函数F的一个下降方向。

牛顿法在最后的收敛阶段有很好的表现，在一定条件下（局部最小值附近的H是正定的且x已接近局部最小值），其可以达到二次收敛。

问题在于，如果H是负定的，且附近有一个局部最大值，牛顿法可能会收敛至该局部最大值。我们可以要求损失函数每一步都是减小的，或者使用如下的混合方法：

2.3 置信区域法和阻尼法

使用一个模型L来拟合F在其临域内的行为，则有

可以看到，L是F的二次泰勒展开式的一个近似。其中，c来近似梯度，而B为近似的海塞矩阵。

对于置信区域法，我们认为这个模型L在一个限定范围  内是足够精确的。如此，就可以得到对应的下降方向

而对于阻尼法，有

阻尼因子  ，该阻尼是用来惩罚大步长的。

算法2.4就可以变为

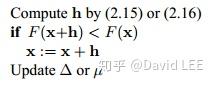
其实就是如果h满足下降条件，则  ；否则  。并且通过调整  或  ，算法可以避免被困在某一点。

考虑到L是对F的临域的模拟，算法更新失败可能就是h（步长）太大了，导致近似不太好。为了衡量L对F的拟合度，定义一个gain ratio

 表示的是损失函数真实下降值和预计下降值之间的比例。由于分母是正数，当分子很小或者为负时，说明此时损失函数没有下降多少甚至还上升来，我们就知道当前的h太大了，导致L不是一个好的近似。

对于置信区域法和阻尼法，常见的更新策略为

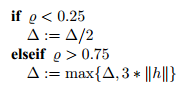
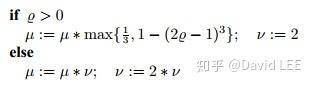
算法对于其中的常数的设置并不敏感，重要的是选择合适的值使得  或  不震荡。

3. 非线性优化算法

前面的损失函数还可以展开为如下形式：

误差函数f(x)的泰勒展开式为：

其中，雅可以矩阵J可以写为

如此一来，损失函数F的微分就可以写成：

将它写成矩阵的形式就有：

最后，F的二阶导（海塞矩阵）为：

3.1 高斯-牛顿法

GN算法基于对误差函数f的线性近似：

因此，损失函数F就变为

L 的梯度和海塞矩阵就是：

而且，如果梯度J是满秩的，那么L的海塞矩阵H就是正定的，说明L(h)拥有唯一的极小值。

通过令L'(h) = 0就可以得到GN算法的解：

可以证明，  确为损失函数F的下降方向：

3.1.1 收敛速度

上一小节提到过，牛顿法可以达到二次收敛。但GN法却不行。为此，我们可以对比这两种方法：

已知这两个等式的右边是一样的，但是等式左边却是不一样的：

显然，如果  ，那么当x接近x*时，  。此时，GN算法可以有二次收敛；但更多时候，GN算法只能达到线性收敛。

3.2 Levenberg-Marquardt 法

LM算法是阻尼法的一种，其步长可以这么算出：

其中，u是拉格朗日算子，它有以下作用：

1. 对于u > 0，可以保证系数矩阵是正定的。这就保证了  必然是一个下降方向；

2. 如果u值很大，那么  . 这是最速下降法下的一小步。这应用在当前迭代距离结果很远的时候；

3. 如果u值很小，那么  ，说明当前的线性近似比较准确。

因此，阻尼因子同时影响了当前迭代的方向和步长。其更新方式在前面已经介绍过了，而初始值可以根据  中元素的大小给出：

对于  的选择，如果起始点x0是对结果的一个比较好的近似，  应该选取一个比较小的值，如  ；否则，可以选择  或者  .

其更新策略同样是计算gain ratio：

其中，

注意到等式最后两项必然是正的，因此，就像前面说的，  的值取决于F的增量。

最后，LM算法的流程如下：

3.2.1 停止条件

首先，当算法到达一个最小值时，有  。因此，第一种停止条件可以为

这里，  是一个很小的正数。

此外，第二种停止条件为在x变化很小时停止：

这说明了在x数值较大时，使用前者（相对量）来说为停止条件；在x数值较小时，使用后者（绝对量）来作为停止条件。

最后，还可以限制迭代次数：

3.3 狗腿法（Powell's dog-leg method)

我们已经知道，GN算法通过求解如下等式（normal equation）得到迭代方向和步长：

而最速下降法则用逆梯度方向作为迭代方向：

其步长可以通过以下方式得到：

对损失函数则有

通过对上式进行求导，并令导数为0可得

这样一来，在更新x的时候，我们就有两个可选的解了：  和  。

而狗腿法是一种置信区域方法。其选取迭代方向和步长的方法如下图所示：

通过上图可以发现，还有一个参数  没有确定。令  ，和

则有

最终的算法如下图所示

---

参考文献：METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS

如果觉得有用，还请点个赞: )