一、前言
该篇博客，主要是对 Homography 矩阵进行一个细致的讲解，主要分为三个部分: 基本介绍、参数设定、公式推导、八点法求解。废话也不多说，那么我们下面就开始吧。

二、基本介绍
单应性矩阵 H \mathbf HH(Homography), 其约束了同一 3D 空间点，在两个 像素平面 \color{red}{像素平面}像素平面 的 2D 齐次坐标 \color{red}{齐次坐标}齐次坐标，现在

如果两个向量方向相同则叉乘为0 向量，不是很明白的朋友可以百度一下向量叉乘的相关知识。经过详细推导，最终可以获得如下公式：

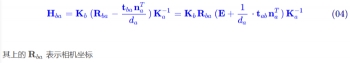
三、参数设定
在相机坐标系下，3D 空间坐标为X，投影到像素坐标系的齐次坐标为p,K为相机内参，分别表示如下，：

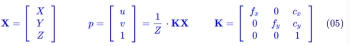
另外 3D 空间点 X所在平面，在相机坐标系得下参数: n表示该平面单位法向量，d表示相机坐标系原点到平面的距离。3D 点 X位于平面{n,d} 上, 其方程表达式为：

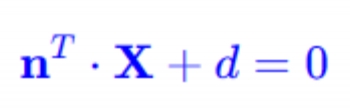
上面我们已经相机系坐标转像素系坐标，那么反过来像素系坐标转相机系坐标公式如下：

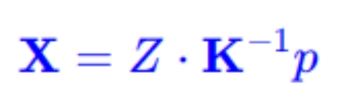
那么这里出现了一个问题。就是说，如果我们知道一个相机坐标系下的三维点与相机内参的时候，根据公式(5)中的第二项是可以求解出对应的像素坐标的。但是在已知像素坐标的情况下，无法求解出该像素点对应相机坐标系下的三维点。根据公式(07)可知，还缺少一个变量 Z, 只要当 Z已知的情况下，才能求解出相机系下对应的三维点。如果知道3D点所在平面参数，也就是(06)式中的{n,d}。那么结合(06),(07)整理得:

也就是，如果知道3D点所在平面的相关参数，那么我们就有办法求解出3D点的深度Z，把 (08)式 代入 (07)式 可得：

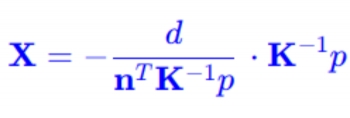
四、公式推导
在前面提到，Homography 是像素坐标系之间的转换。比如(02)表示的就是由像素坐标系 a转到 像素

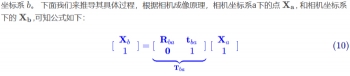
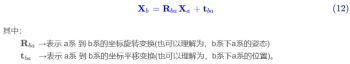
再根据(07)式子，可得

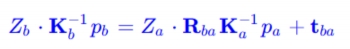
那么继续化简，可得到由 a系下 表达 b系像素：

a系像素 得到 b系像素。那么我们根据前面的推导(08),引入a系中平面参数:

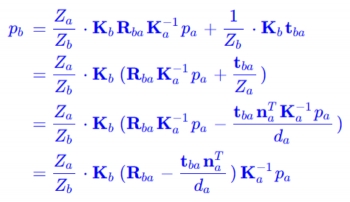
然后再进行符号简化,如下：

我们可以推导出
Rabtab=-tba
把这个带入到(19)式子当中继续推导如下:

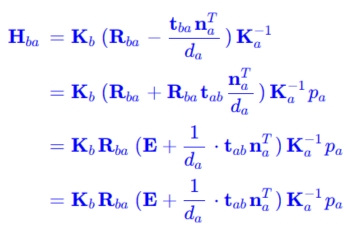
这样结合起来就得到前面(04)式。竟然我们推导出 H \mathbf HH 矩阵，那么如何进行求解呢，如下推导。

五、八点法求解

转化为方程组如下：

进一步转换如下：

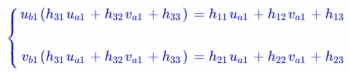
然后我买了转化为一般式:

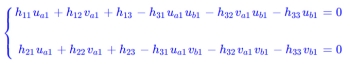
八对特征点的方程组如下：

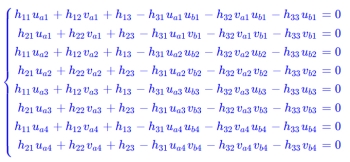
上面的方程组就可以转化成矩阵形式:

六、结语
通过该篇博客，我们已经对 单应性Homography 矩阵进行了详细的讲解。下面我们会结合前面的本质矩阵与基本矩阵进行一个对比，然后讲解他们的适用场景。或者说，什么情况下适合 单应性Homography 矩阵，什么情况下适合本质或者基本矩阵。