第四章 实体识别:图模型基础
实战:https://blog.csdn.net/weixin_42486623/article/details/118347853
代码:https://github.com/daiyizheng/NER-Set/tree/master/hmm
概率模型
机器学习
最重要的任务是根据已观察到的证据(例如训练样本)对感兴趣的未知变量(例如类别标记)进行估计和推测。
概率模型(probabilistic model)
提供了一种描述框架,将任务归结为计算变量的概率分布。在概率模型中,利用已知的变量推测未知变量的分布称为“推断(inference)”,其核心在于基于可观测的变量推测出未知变量的条件分布,即由P ( Y , R , O )或P ( Y , R ∣ O ) 得到P ( Y ∣ O )。
•生成式:计算联合分布P ( Y , R , O )
•判别式:计算条件分布P ( Y , R I O )
符号约定
•y为未知变量的集合,O为可观测变量集合,R为其他变量集合
如何由P ( Y , R , O ) 或P ( Y , R I O )得到P ( Y ∣ O )
思路:直接利用概率求和规则消去变量。
可行性:不可行!即便未知变量集合Y和其他变量集合R中,每个变量只有简单的两种取值,则该方法的时间和空间复杂度为指数级别 O(2^{|Y|+|R|})。
概率图模型分类
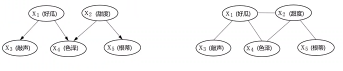
•有向图:贝叶斯网(适合为有单向依赖的数据建模)
•无向图:马尔可夫网(适合实体之间互相依赖的建模
有向图概率
概率乘法公式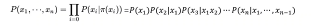
联合概率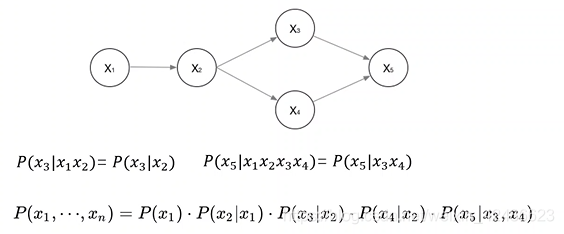
无向图概率
联合概率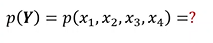
用因子分解将p(Y)写为若干个联合概率的乘积
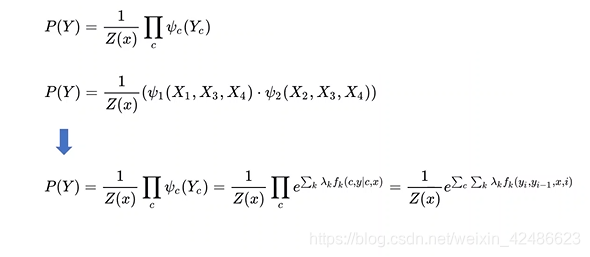
隐马尔可夫模型(Hidden Markoy Model,HMM)
组成
•状态变量:{ y 1 , y 2 … , y n }通常假定是隐藏的,不可被观测的
系统通常在多个状态{ S 1 , S 2 , … , S N }之间切换,因此,状态变量y i 的取值范围(状态空间)通常有N个可能取值的离散空间;
•观测变量:{ x 1 , x 2 , … , x n } 表示第刻的观测值集合
观测变量可以为离散或连续型(本章中只讨论离散型观测变量),x i取值范围为{ o 1 , o 2 , … , o w }即观测变量通常有M个可能取值的离散空间。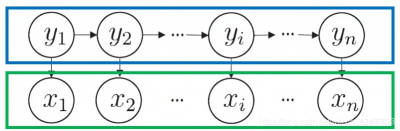
t时刻,观测变量x t的取值仅依赖于状态变量y t时刻,状态y 仅依赖于t − 1 时刻状态y t−1
与其余n − 2 个状态无关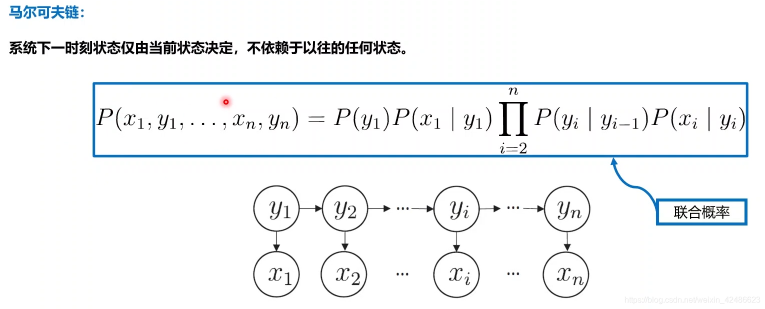
HMM的基本组成
确定一个HMM需要三组参数λ = [ A , B , T ] \lambda=[A,B,T]λ=[A,B,T]
状态转移概率:模型在各个状态间转换的概率
表示在任意时刻t tt,若状态为s i s_i下一状态为s j的概率;
A = [ a i j ] N × N ,a i j = p ( y t + 1 = s j ∣ y t = s i ) , 1 ≤ i , j ≤ N ,1≤i,j≤N
N表示隐藏状态可能取值的离散空间
输出观测概率:模型根据当前状态获得各个观测值的概率
在任意时刻t tt,若状态为s i s_i,则其对应的输出变量为o j的概率;
B = [ b i j ] N × N b i j = p ( x t = o j ∣ y t = s i ) , 1 ≤ i ≤ N , 1 ≤ j ≤ M B=[b_{ij}]_{N \times N} b_{ij}=p(x_t=o_j|y_t=s_i), 1≤i≤N,1≤j≤M表示观测变量可能取值的离散空间
初始状态概率:模型在初始时刻各个状态出现的概率
π = [ π 1 , … , π n ] π i = P ( y 1 = s i , 1 ≤ i ≤ N
P ( x 1 , y 1 , … , x n , y n ) = P ( y 1 ) P ( x 1 ∣ y 1 ) ∏ n i = 2 P ( y i ∣ y i − 1 ) P ( x i ∣ y i )
HMM的生成过程
通过指定状态空间y yy,观测空间X和上述三组参教,就能确定一个隐马尔可夫模型。给定λ = [ A , B , π ] ,它按如下过程生成观察序列:
设置t = 1,并根据初始状态m选择初始状态y 1根据状态y t ,和输出观测概率B选择观测变量取值x t ;根据状态y,和状态转移矩阵A转移模型状态,即确定y t + 1 ;若t < n ,设置t = t + 1,并转到第2步,否则停止。
对于模型A = [ A , B , π ] ,给定观测序列x = { x 1 , x 2 . . X n } x=
•概率计算问题:评估模型和观测序列之间的匹配程度,有效计算观测序列其产生的概率P ( x ∣ A ) ;
•预测问题:根据观测序列“推测”隐藏的模型状态y = { y 1 , y 2 . . … y n },即求得使概率P ( y ∣ x ) 最大的状态序列y;
•参数学习问题:如何调整模型参数λ = [ A , B , π ] 以使得该序列出现的概率P ( x ∣ π ) 最大。
具体应用
根据以往的观测序列x = { x 1 , x 2 . . . , x n } 预测当前时刻最有可能的观测值。
语音识别:根据观测的语音信号推测最有可能的状态序列(即:对应的文字)。
通过数据学习参数(模型训练)。
基于马尔可夫的条件独立性,隐马尔可夫模型的这三个问题均能高效解决(动态规划)
马尔可夫随机场
马尔可夫随机场(Markov Random Field,MRF)
是典型的马尔可夫网
著名的无向图模型
图模型表示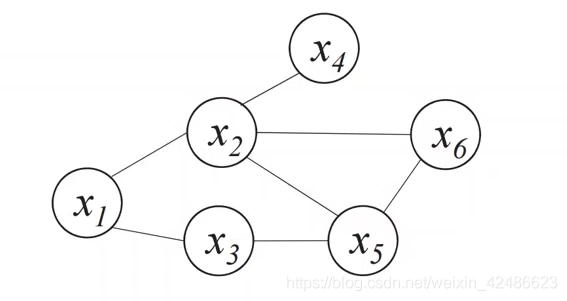
•结点表示变量(集),边表示依赖关系;
•有一组势函数(Potential Functions),亦称“因子”(factor),这是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
分布形式化
使用基于极大团的势函数(因子)
•对于图中结点的一个子集,若其中任意两结点间都有边连接,则称该结点子集为一个“团”(clique)。若一个团中加入另外任何一个结点都不再形成团,则称该团为“极大团”(maximal clique)。
•图中(x1,x2],{x2,x6},{x2,x5,x6]等为团,但{x2,x6)不是极大团,因为(x2,x5,x6}也是一个团。
每个结点至少出现在一个极大团中。
多个变量之间的连续分布可基于团分解为多个因子(势函数)的乘积。
基于极大团的势函数
联合概率分布可以使用极大团定义;
假设所有极大团构成的集合为C ∗ C*C∗,则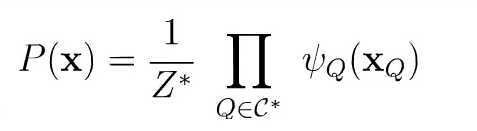
图模型的联合概率分布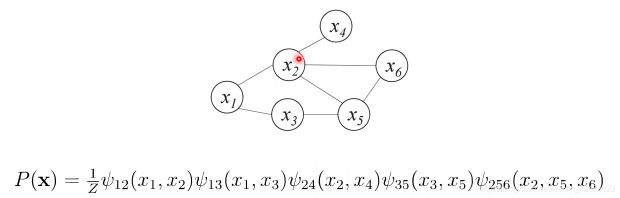
马尔可夫随机场中的分离集
•马尔可夫随机场中得到“条件独立性”。
•借助“分离”的概念,若从结点集A中的结点到B中的结点都必须经过结点集C中的结点,则称结点集A与B被结点集C分离,称C为分离集(separating set)。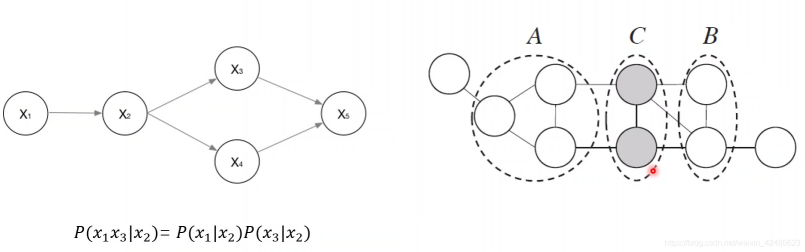
马尔可夫随机场–全局马尔可夫性
借助“分离”的概念,可以得到:
全局马尔可夫性(global Markov property):在给定分离集的条件下,两个变量子集条件独立。
比如,令A,B,C对应的变量集分别为x A , x B , x C 独立,记为x A ⊥ x B ∣ x C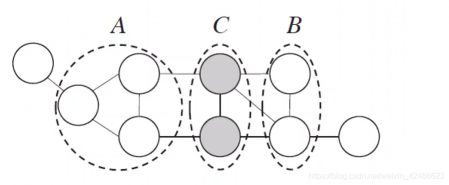
全局马尔可夫性的验证
全局马尔可夫性(global Markov property):在给定分离集的条件下,两个变量子集条件独立。
图模型简化:
图模型的联合概率为: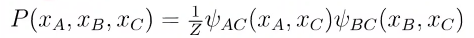
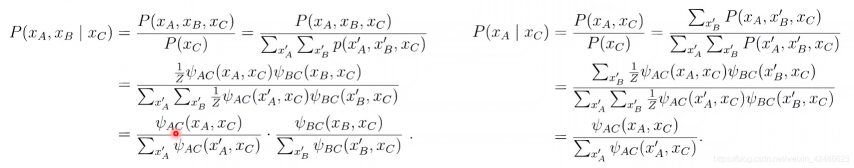
验证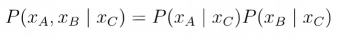
马尔可夫随机场中的条件独立性
由全局马尔可夫性可以导出:
局部马尔可夫性(local Markov property):在给定邻接变量的情况下,一个变量条件独立于其它所有变量;
令V VV为图的结点集,n ( v ) n(v)n(v)为结点v vv在图上的邻接节点,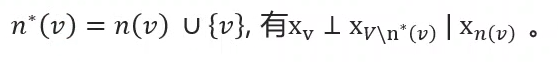
(这是因为n ( v ) n_{(v)}n
(v)
是x v x_vx
v
与x V \ n ∗ ( v ) x_{V\backslash n^*(v)}x
V\n
∗
(v)
的分离集)
成对马尔可夫性(pairwise Markov property):在给定所有其它变量的情况下,两个非邻接变量条件独立。
令V VV为图的结点集,边集为E EE,对图中的两个结点u uu, v vv,若< u , v ∉ E <u,v \notin="" e,有x="" u="" ⊥="" x="" v="" ∣="" \="" <="" ,=""> x_u \bot x_v|x_{V\backslash <u,v> }
马尔可夫随机场中的势函数
势函数φ Q ( x Q ) \varphi_Q(x_Q)φ
Q
(x
Q
)中变量的相关关系,应为非负函数,且在所偏好的变量取值上有较大的函数值。
上图中,假定变量均为二值变量,定义势函数:</u,v></u,v>
说明模型偏好x A x_Ax
A
与x C x_Cx
C
有相同的取值,x B x_Bx
B
与x C x_Cx
C
有不同的取值,换言之,x A x_Ax
A
与x C x_Cx
C
正相关,x B x_Bx
B
与x C x_Cx
C
负相关。所以令x A x_Ax
A
与x C x_Cx
C
相同且x B x_Bx
B
与x C x_Cx
C
不同的变量值,联合概率取值较高。
势函数φ Q ( x Q ) \varphi_Q(x_Q)φ
Q
(x
Q
)的作用是定量刻画变量集x Q x_Qx
Q
中变量的相关关系,应为非负函数,且在所偏好的变量取值上有较大的函数值。
为了满足非负性,指数函数常被用于定义势函数,即:
其中,H Q ( x Q ) H_Q(x_Q)H
Q
(x
Q
)是一个定义在变量x Q x_Qx
Q
上的实值函数,常见形式为: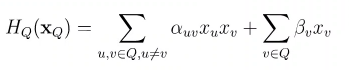
其中,α u v \alpha_{uv}α
uv
和β v β_vβ
v
,是参数,上式第一项考虑每一对结点的关系,第二项考虑单结点。
条件随机场(CRF)
CRF是一种判别式无向图模型,条件随机场对多个变量给定相应观测值后的条件概率进行建模,若令x = x 1 , x 2 . . … xn
为观测序列,y = y 1 , y 2 … , y n y={y_1,y_2…,y_n}为对应的标记序列,CRF的目标是构建条件概率模型P ( y ∣ x ) P(y|x)P(y∣x)。
标记变量y可以是结构型变量,它各个分量之间具有某种相关性。
词性标注任务中,观测数据为单词序列,标记为相应的词性序列,具有线性序列结构;
语法分析任务中,观测数据为单词序列,输出标记是语法树,具有树形结构。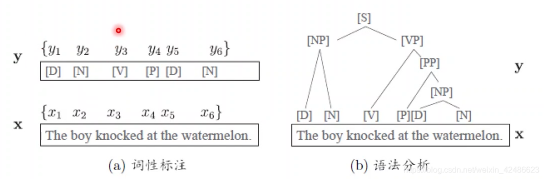
令G = < V , E > G=<v,e>G=<v,e>表示结点与标记变量y yy中元素一一对应的无向图。无向图中,y v y_vy
v
表示与节点v vv对应的标记变量,n ( v ) n_{(v)}n
(v)
表示结点的邻接结点,若图G GG中的每个结点都满足马尔可夫性,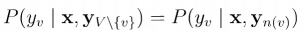
构成条件随机场。
CRF使用势函数和图结构上的团来定义P ( y ∣ x ) P(y|x)P(y∣x)。
考虑链式条件随机场(chain-structured CRF),如下所示: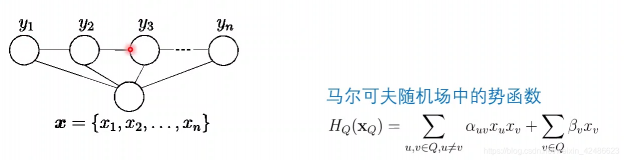
包含两种关于标记变量的团:
相邻的标记变量,即{ y i − 1 , y } ;
单个标记变量,{ y i }
链式条件随机场
条件概率可被定义为: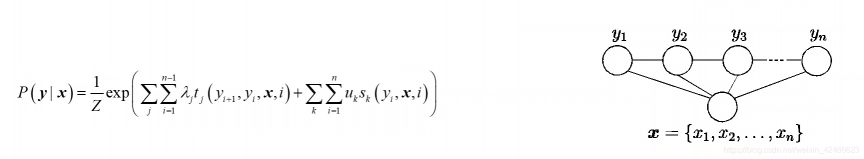
其中,
t i ( y i + 1 , x , i ) :观测序列的两个相邻标记位置上的转移特征函数,用于刻画相邻标记变量之间的相关关系以及观测序列对它们的影响;
s k ( y i , x , i ) :观测序列的标记位置i上的状态特征函数,用于刻画观测序列对标记变量的影响;
λ j , u k 为参数,Z ZZ为规范化因子。
通常特征函数t j t_j,和s k取值为1或0;当满足特征条件时取1,否则为0。</v,e></v,e>
CRF特征函数的直观理解
特征函数通常是实值函数,用于刻画数据中一些大概率成立或者期望成立的经验特性。特征函数本质上是一种规则。
以词性标注任务为例:
函数:
表示第i ii个观测值x为单词’knock’时,相应的标记y , y i + 1 y,y_{i+1}y,y
i+1
很可能分别为[ V ] , [ P ] [V],[P][V],[P]。
其实,该特征函数定义了一个规则,该规则为“ x i “x_i“x
i
为单词knock时,其词性y i y_iy
i
;为动词,且该单词后面一个词的标签需要是介词”。
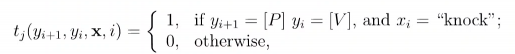
特征函数本质上是一种规则,一个训练好的模型可以看作是多个规则的集合。
示例
MRF与CRF的对比
MRF
使用团上的势函数定义概率
对联合概率建模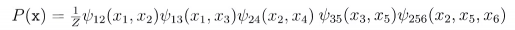
CRF
使用团上的势函数定义概率
有观测变量,对条件概率建模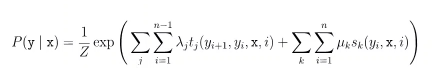






评论(0)
您还未登录,请登录后发表或查看评论