上一章传送门：

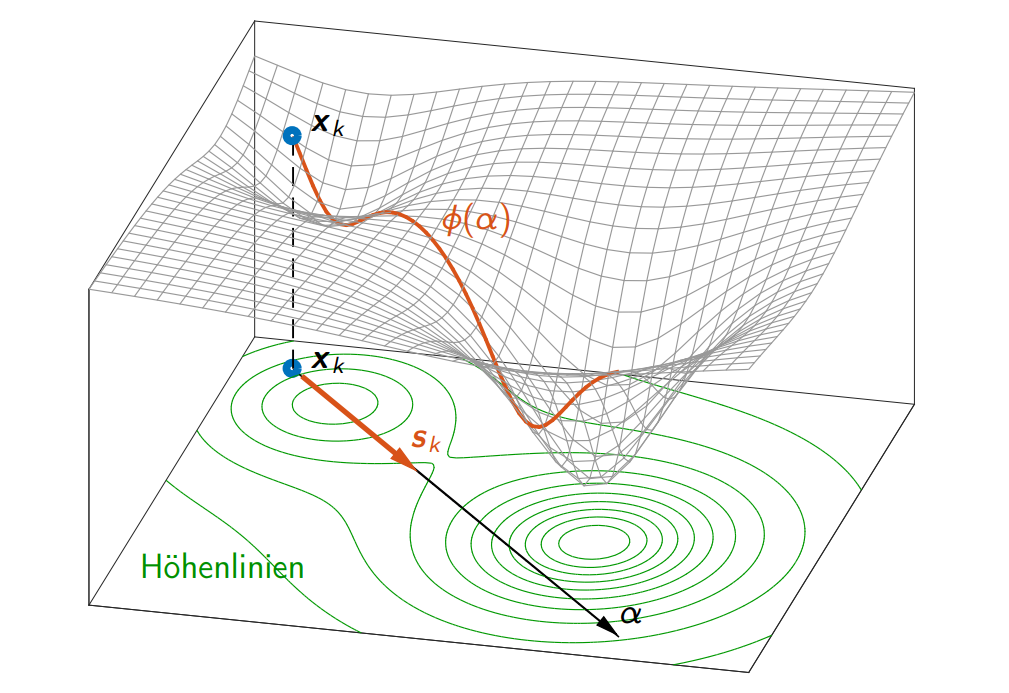
接下来我们探讨如何确定下降方向的向量  。

4.1 梯度法

为了让代价函数沿最快速度方向下降到最小值，除了迭代步长，下降方向也至关重要。确定搜寻方向有许多方案，他们各有特色，依据精度，收敛速度以及计算复杂度相区别。最简单的一种方法，即沿着负梯度方向。那么

(4.1) 

这就是梯度法，往往也被称为梯度下降法，易知满足一阶下降条件

(4.2) 

梯度和等高线  正交，而沿着  位置变动。负的梯度能最小化上一章不等式(3.15)最小化，这也被称为最陡下降方向。

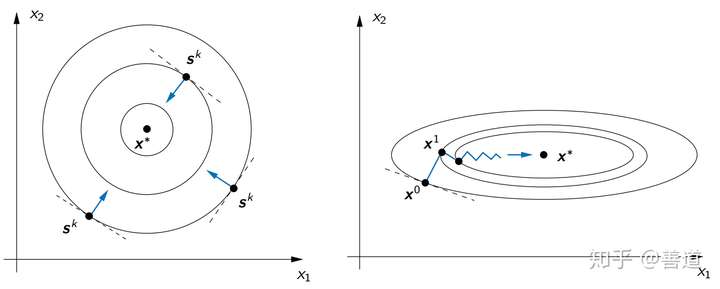
当给定条件较优时(比如  )，负梯度方向直指最小值的中心，从而梯度极快收敛到最小值。而如图右所示，给定条件恶劣时，负梯度方向并不直指最小值中心，下降的过程蜿蜒曲折，收敛速度很慢。

定理4.1 梯度下降收敛速率： 对于二次型函数  ，有正定矩阵  ，其梯度下降法的线搜索精确解的收敛速度满足
(4.3)  
其中  为  的最大最小的特征值。

 表示了  条件的光谱，也直接影响了收敛速度。

总结来说，梯度下降法的优势为简单，而且在Newton法时，有更大的收敛范围。劣势为在条件恶劣时收敛速度很差，而且精度也受限。

4.2 共轭梯度法

这是原有的梯度法的变体，因为计算量没有高过太多，效率和收敛性质却显著优于梯度法。共轭梯度法充分利用了前一步迭代的信息，使得

(4.4) 

(4.5) 

第一步依然是最陡峭的负梯度下降方向，之后的每一步都依赖前一步信息更新，并有修正

(4.6) 

这是由Fletcher和Reeves建议补充的。共轭梯度法基本上放弃了繁琐的矩阵运算，从而也对一些稍微大一点的问题可以应用，使用时也要注意存储器效率。此外梯度法所涉及的二次型  的最优问题中，可以在最多相当于向量  维数  的迭代中收敛。

4.3 Newton法

线搜索的一种特殊情况是，搜索方向的选择正好对应Newton法，此时的搜索方向  被称为Newton方向。首先需要代价函数  在  处近似的二次型模型

(4.7) 

以此来找到最小的  ，通过对  求导，得到

(4.8) 

根据  正定的假设，在  处Newton方向即 

(4.9) 

 的逆矩阵必然也正定，显然也满足下降条件

(4.10) 

Newton方向产生了  自然的迭代过程，因此，Newton法的大多数变体都以 步长作为标准，只有当代价函数  的下降低于边界时，才减小步长。

Newton法实质上是二阶的方法，因为趋近模型有三阶以上的误差。但它对高维系统也相对可靠实用，只要二次近似足够精确。图4.2表现了这个Newton法的方向相比较于最陡峭负梯度方向，更快速逼近最小值。

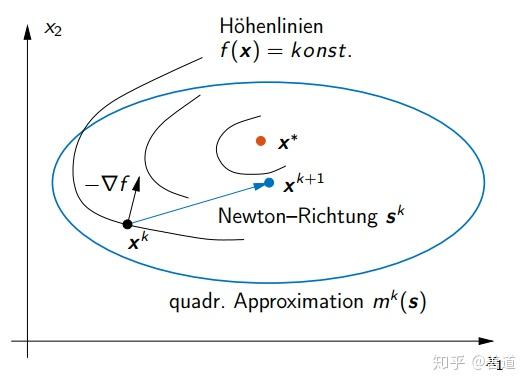
总结来说，Newton法的优势在于平方收敛，速度更快精度比一阶高，但存在局部收敛(不保证对任意  有  )，而且计算Hesse矩阵耗时过多，特别是当维数很高的时候。

为获得全局最小的收敛，Newton法需要至少要保证Hesse矩阵的正定性。还可以通过近似或者Quasi-Newton法来避免Hesse矩阵的计算。

4.4 Quasi-Newton法

Quasi-Newton法是一个非常具有吸引力的对纯Newton法的替代方法，因为可以不用计算Hesse矩阵。反之，采用每次迭代更新逼近Hesse矩阵的方法。这样单步迭代梯度的信息就被充分利用，来提供有关沿搜索方向的二阶导数的信息。

先考虑梯度  在  处线性近似模型

(4.11) 

对于足够小的  就可以近似表示前一步迭代的梯度

(4.12) 

由此可以反推出Hesse矩阵的近似表达 

(4.13)  
不过这样又面临了一个新问题，  有  个待定元素，而却只有  个等式，必须给定更多条件，比如对称矩阵以及  之间的差值。给定了这些条件以后，就可以写出  并得到解析解。一个最有名的更新  的公式即BFGS公式(Broyden, Fletcher, Goldfarb, Shanno)

(4.14) 

其中简写表示  。

起始位置在  ，那么  抑或是最简单的单位矩阵  。

Newton法中还需要计算Hesse矩阵的逆矩阵，所以直接给出等价的逆矩阵  公式就更方便了。

(4.15) 

于是就能得到Quasi-Newton法的搜索方向

(4.16) 

Quasi-Newton法通过很快收敛速度表现抢眼，原则上纯Newton法的收敛速度达不到这种程度，这无外乎向量矩阵运算  远快于计算Hesse矩阵以及它的逆矩阵。另一个相对于纯Newton法的优势即矩阵奇异性的问题不再出现，因为至少在求精确解的时候保证了  的正定性。而且和同样地，Quasi-Newton法对之前共轭梯度法所涉及的二次型  的最优问题中，也可以在最多相当于向量  维数  的迭代中收敛。

4.5 其他数值方法

接下来介绍两种对于无约束最优问题的其他数值方法：置信域法和直接搜索法。

前者类似于线搜索，后者则是不必估算梯度。

4.5.1 置信域法

不同于之前介绍的线搜索法，置信域法构造了代价函数  局部的简单模型  用它来替代原有模型求解局部的最小值。

(4.17) 

因为  只在足够小  的局部精确，寻找  的最小值要受到置信区间的约束  ，近似模型一般也是选用二次型函数

(4.18) 

其中  也之前提到的Hesse矩阵或者相应的近似表达。于是关于  的最优解导向了对于下一个点  的可能的候选方向。若对应的下一个函数值  没有导致先前成本函数值  的充分减小，则置信区间  减小，并且再次求解(4.1)。

当每次迭代不断减小  则新的推算位置和当前位置之间的距离更小了，而  理论上就会指向新的方向。由此发现线搜索法和置信域法的区别，那便是下一步的方向和步长如何选择：

• 线搜索专注  的搜索方向，并需要确定合适的步长 
• 置信域法先划出一个最大可信范围  ，然后同时决定一个合适的方向和步长  ，到达下一个迭代点  ，如有必要，可缩小信任区域并重复搜索。

置信区间  在每个迭代步骤中根据模型  和代价函数  的一致性进行调整。

(4.19) 

 评估了模型和代价函数在一次迭代中的下降的相差程度，所以若  意味着模型和现实符合得很好，于是在下一步中可以继续放大置信区间。而如果  ，那么下一次迭代中必须缩减  。

4.5.2 直接搜索法

之前几个方法都是跟求导相关的，需要用到梯度信息，不过有些时候偏导不存在或者不容易接近或者需要极大计算量，这是一些太复杂或者不再连续可微的问题。可以借助直接搜索/不求导搜索法，只需要借助一些采样点来算出一系列函数值，再来确定迭代点。在非线性最优化中，一个最知名同时又是最简单的方法即Nelder-Mead法。这个算法基于n维空间的单纯形。它由  个点  张开。对  即直线，  即三角形，以此类推。

对由  个点构成的单纯形(Simplex)，同时计算对应坐标的函数值并排序，得到升序

(4.20) 

于是这个算法就用一个新的点替换掉最“坏”的点  ，根据公式

(4.21) 

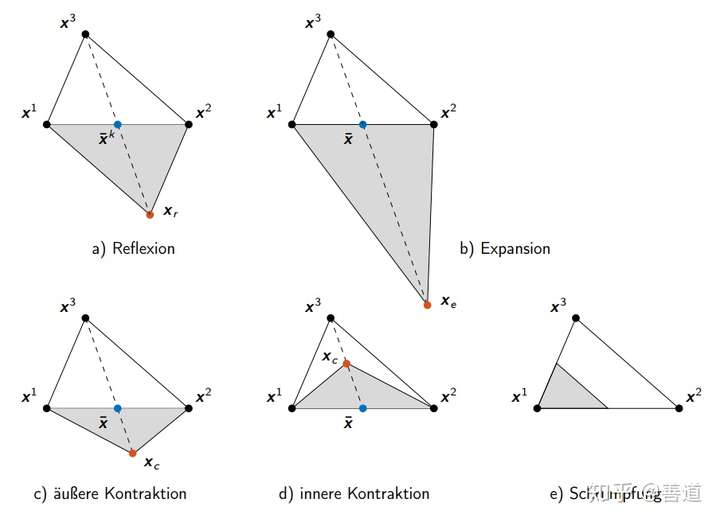
该公式由参数  控制，而  为这个单纯形的重心，根据直线公式可以得到不同的作图法，来获得合适的新的点：反射，扩张，内/外缩以及收缩。

• [a]反射(Reflection)图a)：反射点为  。若  ，则令 
• [b]扩张(Expansion)图b)：若  ，点为  。若  ，则令 。否则令  。
• [c]外缩(äußere Kontraktion)图c)：若  ，则令  。若  ，则令 。否则继续执行步骤收缩步骤[e]。
• [d]内缩(innere Kontraktion)图d)：若  ，则令  。若  ，则令 。否则继续执行步骤收缩步骤[e]。
• [e]收缩(Schrumpfung)图e)：把单纯形压缩在最优点为  。令  ， 

单纯形算法通过不断迭代进行，直到收敛判据达成。单纯形沿着最优方向游走，不过并不能完全保证收敛，也可能会收敛在一个非最优的点。不过实操时，单纯形法往往有很好的结果，而且收敛速度也很快。由于它高鲁棒性，算法又简单，是一个非常常用的算法。

参考文献：

Numerische Optimierung und modellprädiktive Regelung (WS 2019/2020), A. Völz, K. Graichen, Lehrstuhl für Regelungstechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg