学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

现在开始讨论有约束的静态优化问题：

(5.1) $\begin{align} &\min_{\bold x \in \mathbb{R}^n} f(\bold x)\\ &\text{with:}~ g_i(\bold x)=0,~i=1,...,p\\ &\qquad~~ h_j(\bold x)\leq0,j=1,...,q\\ \end{align}$

5.1 一些例子

为了加深对第一章举例的认识，考虑单独的约束条件，作为对无约束情况的扩展补充。

5.1.1 等式约束

例5.1 考虑之前最优问题并带上约束

(5.2) $\begin{align} &\min_{\bold x \in \mathbb{R}^2} f(\bold x)=(x_1-2)^2+(x_2-1)^2\\ &\text{with:}~ g(\bold x)=x_2-2x_1=0\\ \end{align}$

下图展示了直线 $g(\bold x)=0$ 和等高线 $f(\bold x)=const.$ 最优点 $\bold x^*$ 必在直线上，直线而对于 $f(\bold x)=4$ 则有两个交点，显然， $f(\bold x)<4$ 时，两交点不断收缩，汇集于一点 $\bold x^*=[0.8,1.6]^T,f(\bold x^*)=1.8$ 。此时可以看到他们的梯度：

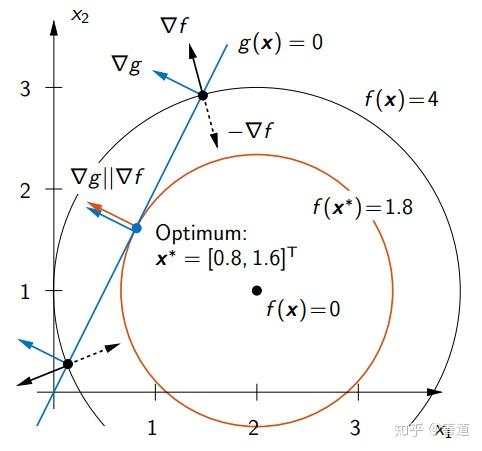
(5.3) $\nabla f(\bold x)=\begin{bmatrix} 2(x_1-2)\\2(x_2-1)\end{bmatrix},\quad\nabla g(\bold x)=\begin{bmatrix} -2\\1\end{bmatrix}$

在所有直线上的非最优点都会让 $\nabla f,\nabla g$ 不共线。即存在一个 $-\nabla f$ (最速下降的梯度)恰好在直线 $g(\bold x)=0$ 上，如此便可在同时遵守约束 $g(\bold x)=0$ 的同时最大地减小代价函数。所以这样的最优点有梯度向量

(5.4) $\nabla f(\bold x)=\begin{bmatrix} -2.4\\1.2\end{bmatrix},\quad \nabla g(\bold x)=\begin{bmatrix} -2\\1\end{bmatrix}$

也就是说两个向量平行的条件为

(5.5) $\nabla f(\bold x^*)+\lambda^* \nabla g(\bold x^*)=\bold0,\quad \lambda^*=-1.2$

这就导出了Lagrange方程

(5.6) $L(\bold x,\lambda)=f(\bold x)+\lambda g(\bold x)$

其中Lagrange乘子联系了两个函数，达到代价函数最优的静态条件即

(5.7) $\nabla _{\bold x} L(\bold x^*,\lambda^*)=\nabla f(\bold x^*)+\lambda^* \nabla g(\bold x^*)=\bold0$

从 $g(\bold x)=0$ 中可以得到一个阶数为 $n+1$ 的等式，来对未知的 $\bold x^*\in \mathbb{R}^n,\lambda^*\in\mathbb{R}$ 构成约束，不过这仅仅是一个必要但不充分的最优条件。

5.1.2 不等式约束

例5.2 考虑之前最优问题带上不等式约束

(5.8) $\begin{align} &\min_{\bold x \in \mathbb{R}^2} f(\bold x)=(x_1-2)^2+(x_2-1)^2\\ &\text{with:}~ h(\bold x)=x_1+x_2-2\leq0\\ \end{align}$

下图展示了处于容许集 $\mathcal{X}_{ad}=\left\{ \bold x \in \mathbb{R}^n:h(\bold x)\leq0\right\}$ 的最优点 $\bold x^*=[1.5,0.5]^T$ 。激活约束后，最优点的梯度 $\nabla f(\bold x^*)=[-1,-1]^T, \nabla h(\bold x^*)=[1,1]^T$ 再次共线。对于其他点，则存在沿着 $h(\bold x)=0$ 的最速梯度下降方向，来保证约束的同时减小代价函数。同理于等式约束也可以构造Lagrange方程

(5.9) $L(\bold x,\lambda)=f(\bold x)+\mu h(\bold x)$

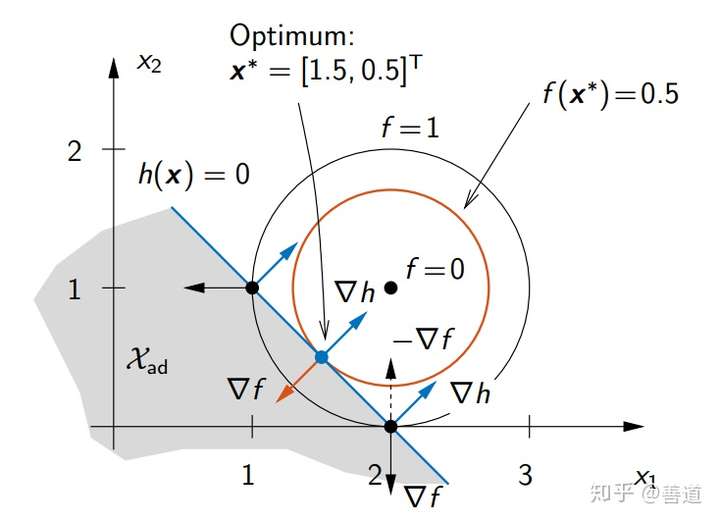
不过区别在于，若取到最优点，则 $h(\bold x^*)\leq0$ 取到等号才能处在容许集里。所以若 $h(\bold x)<0$ ，则 $\bold x^*$ 只能是为代价函数无约束时的最优点，那么满足

(5.10) $\nabla _{\bold x} L(\bold x^*,\mu^*)=\nabla f(\bold x^*)=0,\quad \mu^*=\bold0$

若取到等号，则最优条件和之前等式约束一样。

(5.11) $\nabla _{\bold x} L(\bold x^*,\mu^*)=\nabla f(\bold x^*)+\mu^* \nabla h(\bold x^*)=\bold0$

实际上在最优点处的 $\mu^*$ 的符号非常重要。为明白这一点，我们可以先对 $h(\bold x)$ 一阶泰勒展开

(5.12) $h(\bold x+\bold s)=h(\bold x)+\nabla h(\bold x)^T\bold s+\mathcal{O}(\left| \left| \bold s \right| \right|^2)$

当激活边界条件时 $h(\bold x)=0$ ，若想满足 $h(\bold x+\bold s)\leq0$ ，则必须有足够小 $\bold s$ 满足

(5.13) $\nabla h(\bold x)^T\bold s\leq0$

同理，则对于代价函数展开，若 $\bold x$ 还未达到最优点，一样有

(5.14) $\nabla f(\bold x)^T\bold s<0$

反过来说，如果 $\bold x^*$ 是最优点，并且处在边界 $h(\bold x^*)=0$ ，则不存在任何方向 $\bold s$ 同时满足两个条件。

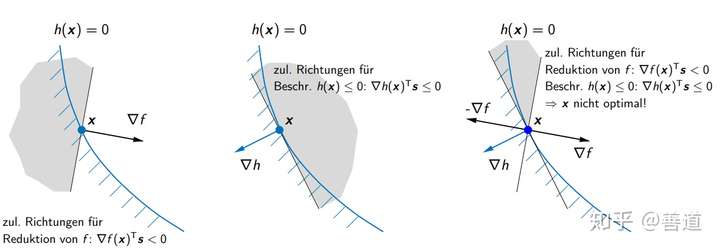
由图可知，阴影区为取 $\nabla f,\nabla h$ 时满足(5.13)(5.14)的时候的 $\bold s$ 方向，取交集以后仍有可以移动的方向。但如果取即 $-\nabla f,\nabla h$ ，则只剩下一个点满足，即最优点。所以

(5.15) $-\nabla f(\bold x^*)=\mu^* \nabla h(\bold x^*)，\quad \mu^* \geq0$

如此才能保证约束下的代价函数下降无处可去。所以 $\mu^*$ 的符号很重要，若 $\mu^*<0$ 则变为 $\nabla f,\nabla h$ 指向同方向，由此产生了半个平面的满足约束的可动方向 $\bold s$ 。

不等式约束的最优条件最后总结为

(5.16) $\exists \mu^* \geq0:\quad\nabla _{\bold x} L(\bold x^*,\mu^*)=\bold0,\quad \mu^* \nabla h(\bold x^*)=\bold0$

容易得到，如果有两个不等式约束，那么按照之前方法可以推广，

(5.17) $\exists \mu_1^*,\mu_2^* \geq0:\nabla _{\bold x} L(\bold x^*, \mu_1^*,\mu_2^*)=\bold0,~ \mu_1^* \nabla h_1(\bold x^*)=\bold0,~ \mu_2^* \nabla h_2(\bold x^*)=\bold0$

5.2 带约束的最优条件

根据之前考察的案例，可知，必须考虑合计 $n+1$ 个等式

(5.18) $g(\bold x^*)=0,\quad \nabla _{\bold x} L(\bold x^*,\lambda^*)=\nabla f(\bold x^*)+\lambda^* \nabla g(\bold x^*)=\bold0$

以便确定唯一的 $\bold x^*\in \mathbb{R}^n,\lambda^*\in\mathbb{R}$ ，以及保证不等式约束

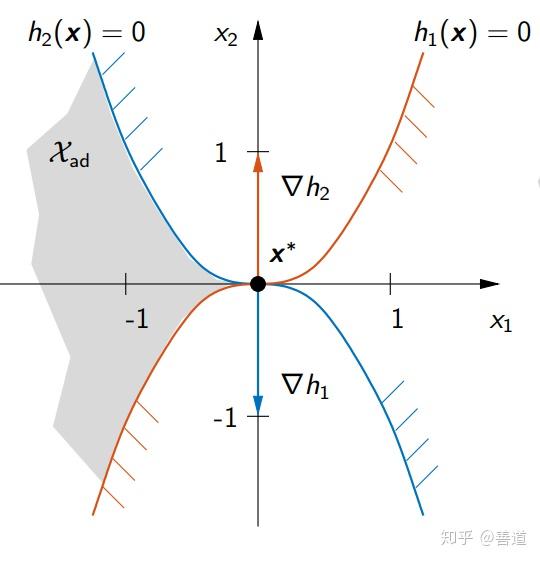
(5.19) $h(\bold x^*)=0,\quad\nabla _{\bold x} L(\bold x^*,\mu^*)=\nabla f(\bold x^*)+\mu^* \nabla h(\bold x^*)=\bold0$

定义5.1 激活不等式约束的集合：给定集合 $\mathcal{A}(\bold x)=\left\{ i=1,...,q|h_i(\bold x )=0\right\}$

$\mathcal{A}(\bold x)$ 即激活了最优问题不等式约束边界条件的集合，边界资格(En: constraint qualification)要求激活不等式约束和等式约束的梯度应当线性无关，即

(5.20) $\text{Rank}\begin{bmatrix} \nabla \bold g(\bold x)\\ \nabla \bold h_{\mathcal{A}(\bold x)}(\bold x) \end{bmatrix}=p+\left| \mathcal{A}(\bold x) \right|$

向量形式的梯度记号表示 $\nabla \bold g(\bold x)=[\nabla g_1(\bold x),...,\nabla g_p(\bold x)]^T$ 以及 $\nabla \bold h_{\mathcal{A}(\bold x)}(\bold x)=[\nabla h_1(\bold x),...,\nabla h_q(\bold x)]^T$ 。边界资格确定了，最多有 $n-p$ 个独立不等式约束可以对最优问题约束。再多的约束只会产生过约束。

不过，边界资格只是描述了约束之间的线性无关性，很多时候也过于保守，或者不是必要的考量。

5.2.1 一阶最优条件

定义5.2 Lagrange函数：最优问题的Lagrange函数为
(5.21) $L(\bold x,\boldsymbol\lambda,\boldsymbol\mu)=f(\bold x)+\boldsymbol\lambda^T\bold g(\bold x)+\boldsymbol\mu ^T\bold h(\bold x)$
其中Lagrange乘子 $\boldsymbol\lambda=[\lambda_1,...,\lambda_p]^T,\boldsymbol\mu=[\mu_1,...,\mu_q]^T$ 而 $\bold g(\bold x)=[ g_1(\bold x),...,g_p(\bold x)]^T$ $\bold h(\bold x)=[ h_1(\bold x),..., h_q(\bold x)]^T$
定理5.1 必要一阶最优条件：若 $\bold x^*$ 为最优问题(5.1)的局部最优解，且满足各项约束条件，若 $f,g_i,h_j$ 都连续可微，那么存在Lagrange乘子 $\boldsymbol\lambda^*=[\lambda_1^*,...,\lambda_p^*]^T,$ $\boldsymbol\mu^*=[\mu_1^*,...,\mu_q^*]^T$ 满足下列条件
(5.22) $\begin{array}{|cc|} \hline \nabla_{\bold x}L(\bold x^*,\boldsymbol\lambda^*,\boldsymbol\mu^*)=\bold0\\ \bold g(\bold x^*)=\bold 0\\ (\boldsymbol\mu ^*)^T\bold h(\bold x^*)=\bold 0\\ h_i(\bold x)\leq 0,i=1,...,q\\ \mu_i ^*\geq0,i=1,...,q\\ \hline \end{array}$

上述定理也被称为Karush-Kuhn-Tucker条件，即KKT。这些补充条件意味着要么激活边界条件有 $h_i(\bold x)= 0$ ，要么没有激活边界条件 $\mu_i ^*=0$ 。而KKT条件成立的前提是 $\bold x^*$ 有边界资格。否则，无法使用KKT条件。

例5.3 考察以下问题

(5.23) $\begin{align} &\min_{\bold x \in \mathbb{R}^2} f(\bold x)=-x_1\\ &\text{with:}~ h_1(\bold x)=x_1^3-x_2\leq0\\ &\qquad~~ h_2(\bold x)=x_1^3+x_2\leq0\\ \end{align}$

作图，不难求得容许集内最优解在 $\bold x^*=[0,0]^T$ 。两端边界条件都激活了，代价函数梯度有

(5.24) $\nabla f(\bold x^*)= \begin{bmatrix} -1\\0 \end{bmatrix},\nabla h_1(\bold x^*)= \begin{bmatrix} 0\\-1 \end{bmatrix},\nabla h_2(\bold x^*)= \begin{bmatrix} 0\\1 \end{bmatrix}$

(5.25) $\nabla_{\bold x}L(\bold x^*,\boldsymbol\mu^*)=\begin{bmatrix} -1\\0 \end{bmatrix}+\mu^*_1 \begin{bmatrix} 0\\-1 \end{bmatrix}+\mu^*_2 \begin{bmatrix} 0\\1 \end{bmatrix}=\bold 0$

上式却是无解的。因为 $\bold x^*=[0,0]^T$ 丧失了边界资格。

5.2.2 二阶最优条件

定理5.2 必要二阶最优条件：若 $\bold x^*$ 为最优问题(5.1)的局部最优解，且满足各项约束条件以及边界资格，并且已经得出满足KKT条件的Lagrange乘子 $\boldsymbol\lambda^*,\boldsymbol\mu^*$ ，若 $f,g_i,h_j$ 都连续二次可微，那么额外有
(5.26) $\bold s^T\nabla^2_{\bold {xx}}L(\bold x^*,\boldsymbol\lambda^*,\boldsymbol\mu^*)\bold s\geq0,\quad \forall\bold s\in \mathcal{C}(\bold x^*,\boldsymbol\mu^*)$ ，其中
(5.27) $\begin{align} \mathcal{C}(\bold x^*,\boldsymbol\mu^*)=\left\{\right . \bold s\in \mathbb{R}^n:& \nabla g_i(\bold x^*)^T \bold s=0,i=1,...,p\\ &\nabla h_j(\bold x^*)^T \bold s=0,j\in\mathcal{A}(\bold x),\mu^*_j>0 \\ &\nabla h_j(\bold x^*)^T \bold s\leq0 ,j\in\mathcal{A}(\bold x),\mu^*_j=0 \left .\right\} \end{align}$

这个定理和之前定理3.1很像，都考虑了二阶Hesse矩阵在最优点处的正定性，不过之前的搜索方向 $\bold s\in \mathbb{R}^n$ ，而现在局限在 $\mathcal{C}(\bold x^*,\boldsymbol\mu^*)$ 里。仅考虑方向 $\bold s$ ，其中来自一阶导数的信息不会显示出它们是否导致代价函数 $f(\bold x^ ∗ +\bold s)$ 减少或增加。

定理5.3 足够最优条件：若 $\bold x^*$ 为许用的最优问题(5.1)的局部最优解，且满足各项约束条件以及边界资格，其对应的的Lagrange乘子 $\boldsymbol\lambda^*,\boldsymbol\mu^*$ 满足KKT条件。若 $f,g_i,h_j$ 都连续二次可微，并且
(5.28) $\bold s^T\nabla^2_{\bold {xx}}L(\bold x^*,\boldsymbol\lambda^*,\boldsymbol\mu^*)\bold s>0,\quad \forall\bold s\ne\bold0\in \mathcal{C}(\bold x^*,\boldsymbol\mu^*)$
那么 $\bold x^*$ 为严格的局部最优。

若Hesse矩阵 $\nabla^2_{\bold {xx}}L$ 有正定性，那么始终满足上述条件。那么凸优化问题对于最优条件的判断可以略去，只需要满足KKT条件足够。于是有

定理5.4 凸优化问题足够最优条件：若函数 $f:\mathbb{R}^n\rightarrow\mathbb{R}$ 和 $h_i:\mathbb{R}^n\rightarrow\mathbb{R}$ 为凸函数，且连续可微，而 $g_i:\mathbb{R}^n\rightarrow\mathbb{R}$ 连续可微且线性。若 $\bold x^*$ 和其对应的的Lagrange乘子 $\boldsymbol\lambda^*,\boldsymbol\mu^*$ 满足KKT条件。那么 $\bold x^*$ 为一个全局最优解。

5.2.3 对Lagrange乘子的解释

除了前面提到的图像上的判断的解释，还有同样直观的数学解释。对一个等式约束的最优问题

(5.29) $\begin{align} &\min_{\bold x \in \mathbb{R}^n} f(\bold x)\\ &\qquad g(\bold x)=0\\ \end{align},\quad \nabla _{\bold x} L(\bold x^*,\lambda^*)=\nabla f(\bold x^*)+\lambda^* \nabla g(\bold x^*)=\bold 0$

为考察Lagrange乘子对最优解 $\bold x^*$ 的影响，考虑在约束上的变动 $\varepsilon$

(5.30) $g(\bold x)=\varepsilon~~\Rightarrow~~\bar g(\bold x(\varepsilon),\varepsilon)=g(\bold x(\varepsilon))-\varepsilon=0$

改写约束为 $\bar g$ ，而变量 $\bold x(\varepsilon)$ 与 $\varepsilon$ 有关，只有当 $\varepsilon=0$ 才是原来的最优点 $\bold x(0)=\bold x^*$ 。求其全微分

(5.31) $d\bar g(\bold x(\varepsilon),\varepsilon)=\nabla_{\bold x} \bar g(\bold x(\varepsilon),\varepsilon)^Td\bold x-d\varepsilon=0\Rightarrow \nabla_{\bold x} \bar g(\bold x(\varepsilon),\varepsilon)^T\frac{d\bold x}{d\varepsilon}=1$

而我们最关心的是对代价函数最小值 $f(\bold x^*)$ 的影响，令 $\bar f(\varepsilon)=f(\bold x(\varepsilon))$

(5.32) $\frac{d \bar f}{d\varepsilon}\bigg|_{\varepsilon=0} =\nabla f(\bold x^*)^T\frac{d\bold x}{d\varepsilon}\bigg|_{\varepsilon=0}=-\lambda^* \nabla_{\bold x} g(\bold x(\varepsilon),\varepsilon)^T\frac{d\bold x}{d\varepsilon}\bigg|_{\varepsilon=0}\Rightarrow\frac{d \bar f}{d\varepsilon}\bigg|_{\varepsilon=0}=-\lambda^*$

可见，Lagrange乘子就是对代价函数最优点变化的度量(敏感度)，同理能得不等式约束的翻版

(5.33) $h(\bold x)\leq\varepsilon\Rightarrow\frac{d \bar f}{d\varepsilon}\bigg|_{\varepsilon=0} =-\mu^*$

对不等式约束在激活边界条件以后取到的 $\mu^*$ 和等式约束一样，描述了代价函数对最优解变化的敏感度。换句话说，一个较大的 $\lambda^*,\mu^*$ 表示放松非常严格的限制条件会促使代价函数 $f$ 显著降低。而且对参数乘子的考察也可以直接建立在原来的约束条件的基础上进行拓展。式子也表现了符号对KKT条件的影响，若 $\mu^*<0\Rightarrow\frac{d \bar f}{d\varepsilon}\bigg|_{\varepsilon=0}>0$ ，即通过离开不等式约束激活边界来进一步减少代价函数可行，因为此时 $\bold x^*$ 还不是最优解，最优解必须满足 $\mu^*\geq0$ 。

参考文献：

Numerische Optimierung und modellprädiktive Regelung (WS 2019/2020), A. Völz, K. Graichen, Lehrstuhl für Regelungstechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg

学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

善道

5.1 一些例子

5.2 带约束的最优条件

为你推荐

路径规划算法学习笔记1——基于搜索

建模——无刷电机数学模型及系统辨识验证

路径规划算法学习Day2

精选点云有用的操作

平衡车gazebo仿真

【自动驾驶】运动规划丨论文分享丨Baidu Apollo EM Motion Planner

关于作者

善道

32

0

0

2

学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

现代控制理论线性系统入门(三)输入输出变量的稳定性

德国人怎么学电机——浅谈电机模型(三)：直流电机(二)电压，转矩和功率

相关推荐

MIT cheetah源码阅读之运动控制状态机（三）

从零开始的分析力学基础 2.质点动力学(4)

自抗扰控制理论（十九）Simulink封装N阶系统LADRC控制器

ROS联合Webots之实现趣味机器人巡线刷圈【基于Tianbot_Mini】

视觉SLAM十四讲学习笔记——ch5 相机与图像

鲁棒控制理论（六）LMI矩阵不等式控制一阶倒立摆系统

热门泡泡

30积分失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

善道

5.1 一些例子

5.2 带约束的最优条件

为你推荐

路径规划算法学习笔记1——基于搜索

建模——无刷电机数学模型及系统辨识验证

路径规划算法学习Day2

精选点云有用的操作

平衡车gazebo仿真

【自动驾驶】运动规划丨论文分享丨Baidu Apollo EM Motion Planner

评论（0）

关于作者

善道

32

0

0

2

学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

现代控制理论线性系统入门(三)输入输出变量的稳定性

德国人怎么学电机——浅谈电机模型(三)：直流电机(二)电压，转矩和功率

相关推荐

MIT cheetah源码阅读之运动控制状态机（三）

从零开始的分析力学基础 2.质点动力学(4)

自抗扰控制理论（十九）Simulink封装N阶系统LADRC控制器

ROS联合Webots之实现趣味机器人巡线刷圈【基于Tianbot_Mini】

视觉SLAM十四讲学习笔记——ch5 相机与图像

鲁棒控制理论（六）LMI矩阵不等式控制一阶倒立摆系统

热门泡泡

30积分 失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分 想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

忘记密码

修改头像

添加你感兴趣的标签

举报类型（必选）

举报详情（选填）

精选点云有用的操作　

30积分失眠，聊聊自己搞ROS的心得体会吧

5积分想买能用ROS2的开发套件。或者开发板