本节介绍非完整系统中的拉格朗日方程，前面遗留的一些问题、或者隐含的问题，大多会在本节得到解决。

4. 非完整系统中的拉格朗日方程

前面的保守场/非保守场的拉格朗日方程推导中，  相互独立是一个很重要的条件，也就是系统必须是完整系统，而在“1.系统约束与虚位移”一节中我们已经提到过，在非完整约束情况下， 并不相互独立，前面介绍的拉格朗日方程推导过程也就失效了，因此本节将重点介绍在  不相互独立情况下（存在非完整约束情况下）的拉格朗日方程推导的问题。

当  相互独立时，有  中  前的系数为零，现在这一条件不成立了，有了  个不独立的  ，能否得到类似前述的拉格朗日方程的式子？我们使用待定乘子法来推导。

假设系统已经具有  个广义坐标，同时受到  个约束：

将约束方程写成变分的形式：

引入  个待定系数  与上式中的  个方程相乘，然后对这  个方程求和

将上式与  联立，可得

虽然在  个  中有  个是不独立的，无法像之前一样直接得出  的系数为零，但我们仍可以适当地选取  个待定系数  使得  的所有系数全等于零，由此可以得出

这  个方程即为非完整系统中的拉格朗日方程，也被称为罗斯方程。将这  个罗斯方程与  个约束方程联立，即可求出  个未知数  。

需要注意的是：

1. 我们是以非完整系统为引子来推导罗斯方程的，但该方程也适用于完整系统，因为完整约束也满足约束方程  ；
2. 不同于前面所有形式的拉格朗日方程，这种形式的拉格朗日方程推导不需要“ 相互独立”这一条件，而是用待定乘数使得系数强制取零，那么在使用此方程时，我们甚至不需要选取独立的坐标来描述系统，广义坐标的选取又变得任意起来。

随着学习的进行，我们对广义坐标的认识也逐渐变得深刻，到这里，我们可以重新思考广义坐标的选取了，它并不一定需要取独立坐标，它可以任意取，只要能够描述系统的位形即可，但还是尽量取独立坐标，这样可以有效减少计算量。

下面的例子我们可以看到广义坐标选取的任意性，并体会到计算量的区别所在。

例2-4. 如图2-6所示单摆，写出其运动方程。

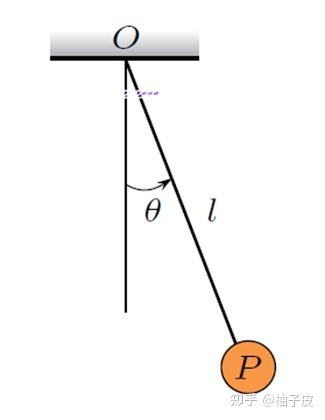
解：

先选取广义坐标为  ；

系统受到的约束为  ；

将约束写成标准形式即  ;

故有  ;

1). 基于完整系统的拉格朗日方程计算：为了使得  相互独立，我们需要判断约束的种类，可以判断出两个约束均为完整约束，因此该问题可以使用完整系统的拉格朗日方程解决，独立坐标数为1，我们可以取一个广义坐标，例如取  ，来继续下一步的动力学计算。

系统的动能和势能可以写为：

系统中不存在非保守外力与阻尼力，故  ;

至此，我们可以列出完整系统的拉格朗日方程：

可得

2). 基于非完整系统的拉格朗日方程计算：就使用原初设定的广义坐标进行计算

系统的动能和势能可以写为：

系统中不存在非保守外力与阻尼力，故  ;

至此，我们可以列出罗斯方程

广义坐标  ：

广义坐标  ：

广义坐标  ：

可得

与约束方程 联立，可以得到

两种方法的结果是一致的，这也印证了前面的说明：罗斯方程也适用于完整系统，带来更大的计算量，但其所需的思维量变少了，无需顾忌约束的类型，也不需要根据独立坐标数选择广义坐标。

还有个问题值得我们思考：推导罗斯方程过程中使用的待定乘子法，其本质是什么？

我们对罗斯方程进行一些倒推，已知

因此有

即

对照拓展哈密顿原理  ，可以发现形式非常类似！实际上，拓展哈密顿定理表征动力学过程使得泛函  取极值；再来观察最上面的式子，它表征在约束条件  下，令泛函  取极值。

有没有什么发现？这种待定乘子法就是高等数学中介绍过的拉格朗日乘数法，待定乘子  就是拉格朗日乘子。

之前内容：

参考文献：F. Daqaq. Dynamics of particles and rigid bodies: a self-learning approach[M]. Hoboken, NJ: John Wiley & Sons, 2018.