相关文章
- K近邻算法和KD树详细介绍及其原理详解
- 朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解
- 决策树算法和CART决策树算法详细介绍及其原理详解
- 线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
- 硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算法详细介绍及其原理详解
- 高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
前言
今天给大家带来的主要内容包括:高斯分布,高斯混合模型,EM算法。废话不多说,下面就是本文的全部内容了!
一、高斯分布
小明是一所大学的老师,一次考试结束后,小明在统计两个班级同学的成绩:
其中,橙色的是一班的成绩,蓝色的是二班的成绩。但是,这次同学们非常调皮,都没有写上自己的名字和班级,这下给小明整不会了。他想:我能不能去猜一猜这些成绩里面,哪些是一班的,而哪些是二班的呢?

根据以往的经验,大多同学的成绩都分布在平均值左右,只有少数的同学考的非常好或者是非常不好,我们把这种概率分布叫做高斯分布:
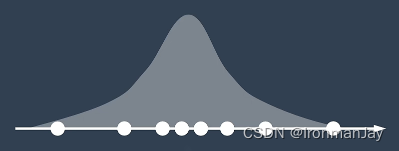
描述高斯分布需要使用到两个参数:
μ
\mu
μ:描述数据的平均值,也被称为均值
σ
2
\sigma^{2}
σ2:描述数据的离散程度,也被称为方差
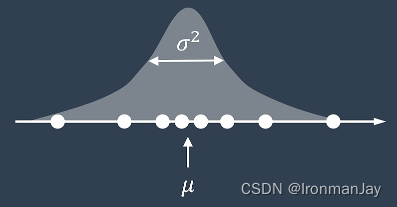
高斯分布的概率密度公式为:
P
(
x
;
μ
,
σ
2
)
=
1
2
π
σ
exp
(
−
(
x
−
μ
)
2
2
σ
2
)
P(x;\mu,\sigma^2)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp(-\dfrac{(x-\mu)^2}{2\sigma^2})
P(x;μ,σ2)=2πσ1exp(−2σ2(x−μ)2)
二、高斯混合模型
现在我们已经清楚了什么是高斯分布,那让我们再回到小明的例子:

因为这是两个班级的成绩,所以小明尝试使用两个高斯分布来拟合:
这样的模型也被称为高斯混合模型。 在这个模型里面:
- 如果我们知道哪些点来自一班或者是来自二班,那么我们就可以计算出来各自班级成绩的平均值和方差
- 如果我们知道各自班级成绩的平均值和方差,我们也可以大概猜出来哪些点是来自一班的,哪些点是来自二班的
这其实是一个鸡生蛋,蛋生鸡的问题:
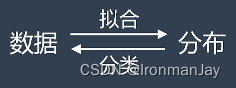
如果我们有数据就可以来拟合分布,如果我们有了概率分布,就可以来判断数据的类别。但是,问题是我们现在什么都没有,应该怎么办呢?
三、EM算法
根据以上分析,我们现在什么数据都没有,还想对成绩进行分类,显然是有难度的。我们应该怎么办呢?既然我们没有数据,不如先做一个合适的假设来确定一部分的值。现在我们假设两个分布是这样的:

而且两个类别的先验概率是相等的。需要注意的是,以上这些都是假设,但是由于这些假设的存在,所以下式的值就是已知的量:
P
(
γ
1
)
=
P
(
γ
2
)
=
0.5
P(\gamma_{1})=P(\gamma_{2})=0.5
P(γ1)=P(γ2)=0.5
3.1 E步骤(Expectation)
现在我们来评估一下每个成绩点是属于哪个班级的,对于第
i
i
i个数据
x
i
x_{i}
xi来说:
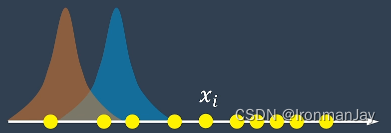
根据贝叶斯定理,
x
i
x_{i}
xi属于一班的概率是这样求的:
γ
i
1
=
P
(
γ
i
∣
x
i
)
=
P
(
x
i
∣
γ
1
)
P
(
γ
1
)
P
(
x
i
∣
γ
1
)
P
(
γ
1
)
+
P
(
x
i
∣
γ
2
)
P
(
γ
2
)
\gamma_{i1}=P(\gamma_i|x_i)=\dfrac{P(x_i|\gamma_1)P(\gamma_1)}{P(x_i|\gamma_1)P(\gamma_1)+P(x_i|\gamma_2)P(\gamma_2)}
γi1=P(γi∣xi)=P(xi∣γ1)P(γ1)+P(xi∣γ2)P(γ2)P(xi∣γ1)P(γ1)
上面的式子看似复杂,但是其中的每一项现在都是已知的,直接计算就可以了。现在已经得到了
x
i
x_{i}
xi属于一班的概率,那么
x
i
x_{i}
xi属于二班的概率就是1减去
x
i
x_{i}
xi属于一班的概率:
γ
i
2
=
P
(
γ
2
∣
x
i
)
=
1
−
γ
i
1
\gamma_{i2}=P(\gamma_{2}|x_{i})=1-\gamma_{i1}
γi2=P(γ2∣xi)=1−γi1
这样我们就可以给每一个点涂上对应的颜色,来表示它们可能属于的班级:
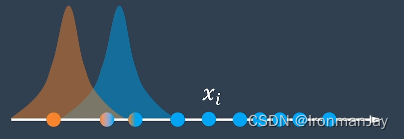
这一步被称为E步骤(Expectation),可以理解为求每一个点属于每个类别的期望值。
3.2 M步骤(Maximization)
此时,我们已经得到了每一个点属于每个班级的可能性,我们就可以重新校准两个班级的高斯分布了,也就是重新计算两个班级的平均值和方差:
- 一班:
μ
1
=
γ
11
x
1
+
γ
21
x
1
+
…
+
γ
N
1
x
N
γ
11
+
γ
21
+
…
+
γ
N
1
σ
1
2
=
γ
11
(
x
1
−
μ
1
)
2
+
…
+
γ
N
1
(
x
N
−
μ
1
)
2
γ
11
+
…
+
γ
N
1
μ1=γ11+γ21+…+γN1γ11x1+γ21x1+…+γN1xNσ12=γ11+…+γN1γ11(x1−μ1)2+…+γN1(xN−μ1)2
- 二班:
μ
2
=
γ
12
x
1
+
γ
22
x
1
+
…
+
γ
N
2
x
N
γ
12
+
γ
22
+
…
+
γ
N
2
σ
2
2
=
γ
12
(
x
1
−
μ
2
)
2
+
…
+
γ
N
2
(
x
N
−
μ
2
)
2
γ
12
+
…
+
γ
N
2
μ2=γ12+γ22+…+γN2γ12x1+γ22x1+…+γN2xNσ22=γ12+…+γN2γ12(x1−μ2)2+…+γN2(xN−μ2)2
同时,也可以更新两个班级的先验概率:
-
一班:
P
(
γ
1
)
=
γ
11
+
…
+
γ
N
1
N
P(\gamma_1)=\frac{\gamma_{11}+\ldots+\gamma_{N1}}{N}
P(γ1)=Nγ11+…+γN1 -
二班:
P
(
γ
2
)
=
γ
12
+
…
+
γ
N
2
N
P(\gamma_2)=\frac{\gamma_{12}+\ldots+\gamma_{N2}}{N}
P(γ2)=Nγ12+…+γN2
这一步被称为M步骤(Maximization),可以理解为,通过当前的数据求出最可能的分布参数。
3.3 EM算法
以上两个步骤合起来就是EM算法。当然,算法还没有结束,我们现在只是通过E和M两个步骤求出了两个班级的成绩分布的新的平均值和方差:
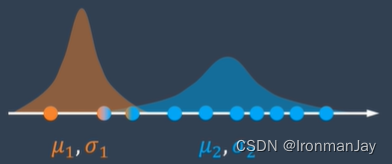
后面的工作就是重复E和M两个步骤:
- E步骤:根据两个班级的成绩分布更新点属于两个班级的可能性
- M步骤:更新两个班级的成绩分布的平均值和方差
一直重复以上两个步骤,直到两个成绩分布收敛不再被更新:
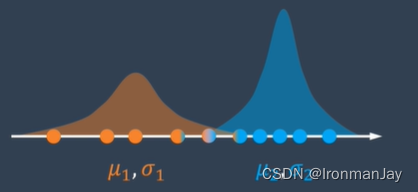
这样我们就得到了一个还不错的分类效果:

虽然和真实数据相比仍然有误差,不过也可以猜的八九不离十了:

这样,通过EM算法,小明的问题就可以被解决了。
总结
以上就是本文的全部内容了,学习EM算法还需要一些概率论与数理统计和高等数学的相关知识,所以读者最好提前温习一下。学习机器学习避免不了学习高等数学、线性代数、概率论与数理统计和矩阵论,所以读者一定要好好学习这几门课程!






评论(0)
您还未登录,请登录后发表或查看评论