无监督提取特征

  • 特征提取是无监督学习中很重要且很基本的一项任务，常见形式是训练一个编码器将原始数据集编码为一个固定长度的向量。自然地，我们对这个编码器的基本要求是：保留原始数据的（尽可能多的）重要信息

重构 → 最大化互信息

  • 自编码器：我们怎么知道编码向量保留了重要信息呢？一个很自然的想法是这个编码向量应该也要能还原出原始图片出来，所以我们还训练一个解码器，试图重构原图片，最后的 loss 就是原始图片和重构图片的 mse。这导致了标准的自编码器的设计
  • 重构的思考：然而，值得思考的是 “重构” 这个要求是否合理？首先，我们可以发现通过低维编码重构原图的结果通常是很模糊的，这可以解释为损失函数 mse 要求 “逐像素” 重建过于苛刻。又或者可以理解为，对于图像重构事实上我们并没有非常适合的 loss 可以选用，最理想的方法是用对抗网络训练一个判别器出来，但是这会进一步增加任务难度。其次，一个很有趣的事实是：我们大多数人能分辨出很多真假币，但如果要我们画一张百元大钞出来，我相信基本上画得一点都不像。这表明，对于真假币识别这个任务，可以设想我们有了一堆真假币供学习，我们能从中提取很丰富的特征，但是这些特征并不足以重构原图，它只能让我们分辨出这堆纸币的差异。也就是说，对于数据集和任务来说，合理的、充分的特征并不一定能完成图像重构
  • 互信息：上面的讨论表明，重构不是好特征的必要条件。好特征的基本原则应当是 “能够从整个数据集中辨别出该样本出来”，也就是说，提取出该样本（最）独特的信息。如何衡量提取出来的信息是该样本独特的呢？我们用 “互信息” 来衡量

    最大化互信息

    互信息

  • 我们用 X 表示原始图像的集合，Z 表示编码向量的集合，p(z|x)表示 x 所产生的编码向量的分布，我们设它为高斯分布，它与 VAE 中的 encoder 相同，都是输入 x，输出 z 的一个高斯分布，该高斯分布满足各分量独立。那么可以用互信息来表示 X,Z的相关性

    I(X,Z) = \iint p(z|x){p}(x)\log \frac{p(z|x)}{p(z)}dxdz

    其中，p(x) 为原始数据的分布，p(z) 是在 p(z|x)给定之后整个 ZZ 的分布，即

    p(z) = \int p(z|x){p}(x)dx

    一个好的特征编码器，应该要使得互信息尽量地大，即

    p(z|x) = \max_{p(z|x)} I(X,Z)

    先验分布

  • 相对于自编码器，变分自编码器同时还希望隐变量服从标准正态分布的先验分布，这有利于使得编码空间更加规整，甚至有利于解耦特征，便于后续学习。因此，在这里我们同样希望加上这个约束
  • Deep INFOMAX 论文中通过类似 AAE (Adversarial Autoencoder) 的思路通过对抗来加入这个约束 (i.e. 引入 Discriminator 衡量两个分布之间的散度，Encoder 则作为 Generator 去最小化 Discriminator 得到的散度)，但众所周知对抗是一个最大最小化过程，需要交替训练，不够稳定，也不够简明。这里提供另一种更加端到端的思路：设q(z)为标准正态分布，我们去最小化 p(z) 与先验分布q(z) 的 KL 散度：

    KL(p(z)\Vert q(z))=\int p(z)\log \frac{p(z)}{q(z)}dz

    损失函数

    简化先验项

  • 将最大化互信息与接近先验分布的目标函数加权混合起来，我们可以得到最小化的总目标：

    \begin{aligned}p(z|x) =& \min_{p(z|x)} \left\{- I(X,Z) + \lambda KL(p(z)\Vert q(z))\right\}\\ =&\min_{p(z|x)}\left\{-\iint p(z|x){p}(x)\log \frac{p(z|x)}{p(z)}dxdz + \lambda\int p(z)\log \frac{p(z)}{q(z)}dz\right\}\end{aligned}

    将上式稍加变换得到：

    p(z|x) =\min_{p(z|x)}\left\{\iint p(z|x){p}(x)\left[-(1+\lambda)\log \frac{p(z|x)}{p(z)} + \lambda \log \frac{p(z|x)}{q(z)}\right]dxdz\right\}

    注意上式正好是互信息与\mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]的加权求和，而 KL(p(z|x)∥q(z)) 这一项是可以算出来的，它正好是 VAE 的那一项 KL 散度，即

    \begin{aligned}&KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)\\ =&\mathbb E_{x\sim N(\mu,\sigma^2)}\left[\log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-x^2/2}/\sqrt{2\pi}}\right]\\ =&\mathbb E_{x\sim N(\mu,\sigma^2)}\left[ \log \left\{\frac{1}{\sqrt{\sigma^2}}\exp\left\{\frac{1}{2}\big[x^2-(x-\mu)^2/\sigma^2\big]\right\} \right\}\right]\\ =&\frac{1}{2}\mathbb E_{x\sim N(\mu,\sigma^2)} \Big[-\log \sigma^2+x^2-(x-\mu)^2/\sigma^2 \Big]\\ =&\frac{1}{2}\mathbb E_{x\sim N(\mu,\sigma^2)} \Big[-\log \sigma^2+(1-1/\sigma^2)x^2+2\mu x/\sigma^2-\mu^2/\sigma^2 \Big]\\ =&\frac{1}{2}\Big[-\log \sigma^2+(1-1/\sigma^2)(\mu^2+\sigma^2)+2\mu^2/\sigma^2-\mu^2/\sigma^2 \Big]\\ =&\frac{1}{2}\Big(-\log \sigma^2+\mu^2+\sigma^2-1\Big) \end{aligned}

    KL\Big(N(\mu,\text{diag}(\sigma^2))\Big\Vert N(0,I)\Big)=\frac{1}{2} \sum_{i=1}^d \Big(\mu_{i}^2 + \sigma_{i}^2 - \log \sigma_{i}^2 - 1\Big)

  • 至此所以我们已经成功地解决了整个 loss 的一半，可以写为

    p(z|x) =\min_{p(z|x)}\left\{-\beta\cdot I(X,Z)+\gamma\cdot \mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]\right\}

    下面我们主攻互信息这一项

    互信息本质

  • 互信息是 p(z|x){p}(x) 和 p(z)p(x) 这两个分布的 KL 散度

    I(X,Z)=KL(p(z|x)p(x)∥p(z)p(x))

    注意 KL 散度理论上是无上界的，我们要去最大化一个无上界的量，这件事情有点危险，很可能得到无穷大的结果。所以，为了更有效地优化，我们抓住 “最大化互信息就是拉大 p(z|x){p}(x)和 p(z)p(x) 之间的距离” 这个特点，我们不用 KL 散度，而换一个有上界的度量：JS 散度，它定义为

    JS(P,Q) = \frac{1}{2}KL\left(P\left\Vert\frac{P+Q}{2}\right.\right)+\frac{1}{2}KL\left(Q\left\Vert\frac{P+Q}{2}\right.\right)\in[0,\frac{1}{2}\log2]

    我们最大化它的时候，同样能起到类似最大化互信息的效果，但是又不用担心无穷大问题。于是我们用下面的目标取代目标式：

    p(z|x) =\min_{p(z|x)}\left\{-\beta\cdot JS\big(p(z|x){p}(x), p(z){p}(x)\big)+\gamma\cdot \mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]\right\}

    攻克互信息

  • 在 f-GAN 中，我们知道一般的f 散度的局部变分推断为

    {D}_f(P\Vert Q) = \max_{T}\Big(\mathbb{E}_{x\sim p(x)}[T(x)]-\mathbb{E}_{x\sim q(x)}[g(T(x))]\Big)

    其中，{D}_f(P\Vert Q)为P,Q间的 f 散度，g 为 f的共轭函数，T(x)可以用 NN 逼近 (即 f-GAN 中的 Discriminator). 对于 JS 散度，给出的结果是

    JS(P,Q) = \max_{T}\Big(\mathbb{E}_{x\sim p(x)}[\log \sigma(T(x))] + \mathbb{E}_{x\sim q(x)}[\log(1-\sigma(T(x))]\Big)

    它其实就是 vanilla GAN 中的V(G,D)，代入 p(z|x)p(x), p(z)p(x)就得到

    \begin{aligned}&JS\big(p(z|x){p}(x), p(z){p}(x)\big)\\=& \max_{T}\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T(x,z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T(x,z))]\Big)\end{aligned}

    要想计算出上述 JS 散度，就需要引入一个判别网络σ(T(x,z))，x 及其对应的 z 视为一个正样本对，x 及随机抽取的 z 则视为负样本，然后最大化似然函数，等价于最小化交叉熵

  • 这样一来，通过负采样的方式，我们就给出了估计 JS 散度的一种方案，从而也就给出了估计 JS 版互信息的一种方案，从而成功攻克了互信息。现在，具体的 loss 为

    \begin{aligned}&p(z|x),T(x,z) \\ =&\min_{p(z|x)}\Big\{-\beta\cdot\max_{T(x,z)}\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T(x,z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T(x,z))]\Big)\\ &\qquad\qquad\qquad+\gamma\cdot \mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]\Big\}\\ =&\min_{p(z|x),T(x,z)}\Big\{-\beta\cdot\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T(x,z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T(x,z))]\Big)\\ &\qquad\qquad\qquad+\gamma\cdot \mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]\Big\}\end{aligned}

    总结一下， KL 散度那一项就是 VAE 中的正则项，它要求 encoder 输出的高斯分布接近标准高斯分布，损失函数照搬 VAE 的即可：

    KL\Big(N(\mu,\text{diag}(\sigma^2))\Big\Vert N(0,I)\Big)=\frac{1}{2} \sum_{i=1}^d \Big(\mu_{i}^2 + \sigma_{i}^2 - \log \sigma_{i}^2 - 1\Big)

    对于互信息那一项，我们首先将互信息表示为 KL 散度的形式，然后将 KL 散度替换为 JS 散度，最终通过与 vanilla GAN 相同的方法，用 Discriminator 衡量 JS 散度，然后用 encoder 最大化 JS 散度从而最大化 encoder 输入和输出之间的互信息，与 vanilla GAN 不同的是，这里 Discriminator 和 encoder 的优化方向相同，都是使得 V(G,D) 最大。在具体实现上，首先我们随机选一张图片 x，通过编码器就可以得到 z 的均值和方差，然后重参数就可以得到 z_x，这样的一个(x,z_x)对构成一个正样本；负样本呢？为了减少计算量，我们直接在 batch 内对图片进行随机打乱，然后按照随机打乱的顺序作为选择负样本的依据，也就是说，如果 x 是原来 batch 内的第 4 张图片，将图片打乱后第 4 张图片是\hat x，那么 (x,z_x)就是正样本，(\hat x,z_x)就是负样本。并且由于 encoder 和 Discriminator 的优化目标相同且都需要相似的计算过程 (e.g. 它们都需要对输入 x 进行编码)，因此我们可以共享 encoder 和 Discriminator 的部分结构，例如将 x用 encoder 抽取出的特征图替代 (实际上，我们甚至可以直接用 (z_x,z_x)作为正样本，(z_{\hat x},z_x)作为负样本，这是因为就算用原图 x，Discriminator 最终也是要不断地将 x 降维，然后和 z 交互，最终输出一个数来的，用全局特征 z 来代替样本 x相当于共享了两者的编码器)

    Deep InfoMax 论文中除了上面介绍的 Jensen-Shannon MI estimator (JSD)，还给出了其他两种对互信息的估算方法，包括 a lower-bound to the MI based on the Donsker-Varadhan representation of the KL-divergence (DV-based objective) (论文中 (2) 式，证明可参考 Mine: mutual information neural estimation 附录) 和 Noise-Contrastive Estimation (infoNCE) (论文中 (5) 式，可参考 Representation learning with contrastive predictive coding). 论文中提到 JSD 比 DV-based objective 在实际应用中效果更好，并在实验中重点比较了 JSD 和 infoNCE 的效果，发现 infoNCE 在下游任务上的效果经常好于 JSD (this effect diminishes with more challenging data)，但 infoNCE 和 DV 相比 JSD 需要更多的负样本数量 (samples from p(z)p(x)p(z))，JSD 对负样本数量不敏感

    从全局到局部

  • 上面的做法，实际上就是考虑了整张图片之间的关联，也就是衡量的是输入图像 x 和隐变量 z 之间的互信息，但是我们知道，图片的相关性更多体现在局部中（也就是因为这样所以我们才可以对图片使用 CNN）。换言之，图片的识别、分类等应该是一个从局部到整体的过程。因此，有必要把 “局部互信息” 也考虑进来

通过 CNN 进行编码的过程一般是：
\text{原始图片}x\xrightarrow{\text{多个卷积层}} h\times w\times c\text{的特征} \xrightarrow{\text{卷积和全局池化}} \text{固定长度的向量}z
我们已经考虑了 x 和 z的关联，那么中间层特征（feature map）和 z 的关联呢？我们记中间层特征为 {C_{ij}(x)|i=1,2,…,h;j=1,2,…,w} 也就是视为 h×w个向量的集合，我们也去算这h×w 个向量跟z_x的互信息，称为 “局部互信息”。换个角度来想，也可以这样理解：局部互信息的引入相当于将每个小局部也看成了一个样本，这样就相当于原来的 1 个样本变成了 1+hw个样本，大大增加了样本量，所以能提升效果。同时这样做也保证了图片的每一个 “角落” 都被用上了，因为低维压缩编码，比如 32×32×3编码到128维，很可能左上角的8×8×3>128的区域就已经能够唯一分辨出图片出来了，但这不能代表整张图片，因此要想办法让整张图片都用上。估算方法跟全局是一样的，将每一个 C_{ij}(x)与z_x拼接起来得到[C_{ij}(x),z_x]，相当于得到了一个更大的 feature map，然后对这个 feature map 用多个 1\times1 的卷积层来作为局部互信息的估算网络T_{local}(i.e. Discriminator)。负样本的选取方法也是用在 batch 内随机打算的方案

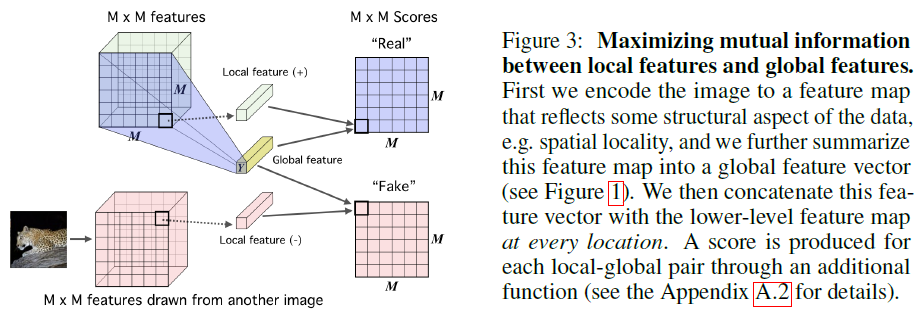
  • 现在，加入局部互信息的总 loss 为

\begin{aligned}&p(z|x),T_1(x,z),T_2(C_{ij}, z)=\min_{p(z|x)}\Big\{\\ &\quad-\alpha\cdot\max_{T_1(x,z)}\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T_1(x,z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T_1(x,z))]\Big)\\ &\quad-\frac{\beta}{hw}\sum_{i,j}\max_{T_2(C_{ij}, z)}\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T_2(C_{ij},z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T_2(C_{ij},z))]\Big)\\ &\quad+\gamma\cdot \mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]\Big\} \\&=\min_{p(z|x),T_1(x,z),T_2(C_{ij}, z)}\Big\{\\ &\quad-\alpha\cdot\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T_1(x,z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T_1(x,z))]\Big)\\ &\quad-\frac{\beta}{hw}\sum_{i,j}\Big(\mathbb{E}_{(x,z)\sim p(z|x){p}(x)}[\log \sigma(T_2(C_{ij},z))] + \mathbb{E}_{(x,z)\sim p(z){p}(x)}[\log(1-\sigma(T_2(C_{ij},z))]\Big)\\ &\quad+\gamma\cdot \mathbb{E}_{x\sim{p}(x)}[KL(p(z|x)\Vert q(z))]\Big\}\end{aligned}

References