三维空间的刚体运动
点与坐标系
旋转矩阵
旋转向量和欧拉角
四元数
点与坐标系
2D的情况:用两个坐标加旋转角表达
3D的情况:?
在描述3D的情况前,可以先描述一些基本概念:
坐标系、点、向量、向量的坐标
坐标系(参考系)任何运动都是相对的,需要一个参考系。只能说哪个东西在某个参考系下看起来是怎样的运动、它位于什么位置等等。参考系一般是由三个轴组成的迁移空间的一个基,基向量,正常情况下这三个基向量都是彼此正交的。有两种不同的定义方式,左手系和右手系,除大拇指外的四个指头从x转到y,大拇指的方向如果向上就是右手系,反之左手系,两种方式没有优劣之分,在这里我们采用右手系。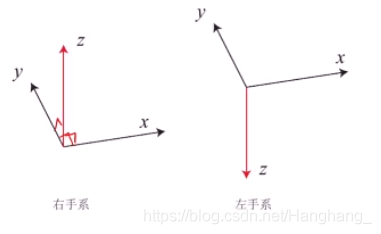
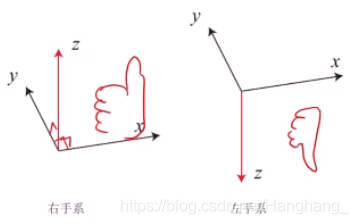
若要讨论运动,一般是在坐标系讨论的。而且往往会讨论到几个坐标系,有一些坐标系是固定的,一些坐标系是运动的,一般我们关心多少个物体就考虑多少个坐标系。
比如一个相机在世界当中运动,这时候建立两个坐标系。一个是世界坐标系,一个是相机坐标系。
我们要关心的是这两个坐标系之间的变换是怎么样子的。
例如:建立一个点P,这个点在两个坐标系的位置是不一样的,已知P在世界坐标轴的位置,如何去变换到相机坐标轴下的坐标?
如果是一个机器人的话,那这样会更加复杂,比如机器人本体需要建立一个坐标系,机械臂也需要建立一个坐标系,激光雷达也会有一个坐标系。如果知道每一个坐标系的位置坐标关系,就可以很方便地讨论某一个数据在一个坐标系下的运动情况,在另一个坐标系下的运动情况。
在世界坐标系中,由于坐标系由三个互相正交的向量基组成,向量P可以由三个基的线性组合所构成,且唯一。向量表示为:
然后我们就可以讨论同样的一个P,它在另一个坐标系下是如何表示的,这几个坐标之间是如何 这是本节所要讨论的问题。
向量的运算可由坐标运算表达
加法和减法
其中两向量的加法和减法,可以使用平行四边形法则来表示。
内积 : 点乘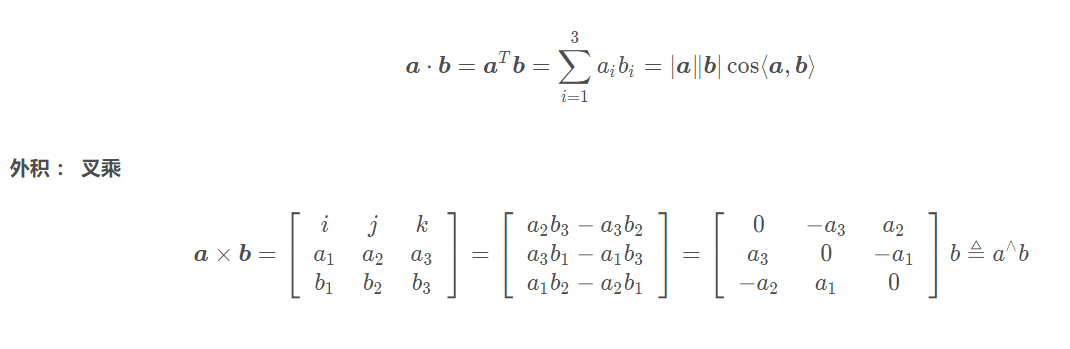
会根据右手法则得到一个同时与a和b都垂直的一个向量
这个运算也可以由行列式的方式写出来,右式由i,j,k的分量表示。
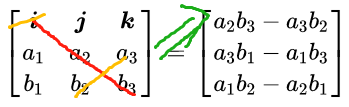
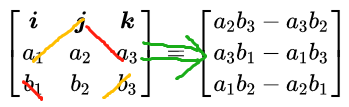
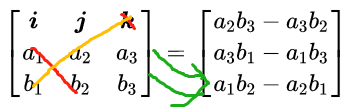

在了解向量得到运算之后,来探讨以下问题。
如何描述坐标系与坐标系之间的变化?
如何计算同一个向量在不同坐标系里的坐标?
坐标系之间的变化可以直观地表示为:原点间的平移+三个轴的旋转
那么平移是向量,旋转是什么?
旋转矩阵
考虑一次旋转:
坐标系(e1,e2,e3)发生了旋转,变成(e1`,e2`,e3`)
向量α不动,那么它的坐标如何变化?


旋转向量和欧拉角
旋转矩阵R有九个元素,但仅有三个自由度,能否以更少的元素表达旋转?
答案是肯定的,除了旋转矩阵,还有旋转向量、欧拉角以及四元数可以表达旋转。
旋转向量:方向为旋转轴,长度为转过的角度 ;称为角轴/轴角(Angle Axis)或旋转向量(Rotation Vector)
旋转向量与矩阵不同:仅有三个量,无约束,更直观
假如知道旋转轴和转过的角度,要计算旋转矩阵R,则需要用到罗德里格斯公式:
**欧拉角:**将旋转分解为为三个方向上的转动,轴可以是定轴或动轴(转之前的x轴或转之后的x轴),顺序亦可不同。常见的有yaw-pitch-roll(Z-Y-X)。使用欧拉角优点是非常直观,缺点是定义非常混乱,使用比较复杂,还有一个严重的问题就是万向锁(Gimbal Lock),在某种特定的情况下,会出现奇异性,就是减少掉一个自由度。
比如 Yaw-Pitch-Roll 顺序下,当Pitch为90度时,存在奇异性,即yaw和roll方向一样。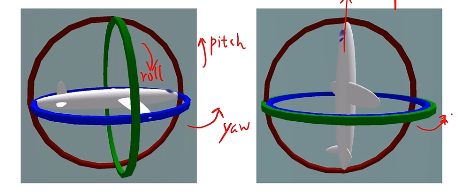
由于万向锁的存在,欧拉角不适合插值或迭代,多用于人机交互中,可以证明:仅用三个实数表达旋转时,不可避免地存在奇异性问题,所以SLAM中也很少用欧拉角表示姿态。
四元数
四元数是一种既比较节省空间又不带奇异性的表达旋转的方法。
在2D情况下,可用 单位复数表达旋转。复数是二维的,在复平面上,实数可用一条从左到右的直线表示,而虚数可以由一条从小至上的直线表示。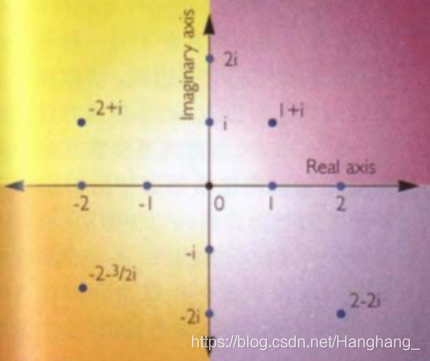








评论(0)
您还未登录,请登录后发表或查看评论