现代控制理论线性系统入门(七)输入输出解耦的控制器设计

上一章传送门：

在利用状态方程设计MIMO的能控标准型时，闭环系统的动态是完全不考虑输出变量 $\mathbf{y}$ 而直接预给的，MIMO系统的输出动态可能会因为状态变量之间的耦合导致变换到能控标准型时无法保证期望的系统动态。这就是输入输出变量解耦的必要性，这样输入和输出就不会耦合在一起，期望的动态会被直接加在输出上。

接下来假设，输入控制量 $\mathbf{u}\in \mathbb{R}^m$ 输出变量 $\mathbf{y}\in \mathbb{R}^p$ 具有相同的维度，即 $m=p$ 。这种控制器的设计方法其实最开始源自Falb和Wolovich，还有更多的方法论都是基于输入输出线性化的非线性系统的理论。

7.1 相对微分度

要实现输入输出的解耦，需要用到相对微分度(relativer Grad)的概念。考察一个MIMO的系统

(7.1) $\begin{align} \mathbf{\dot x}&=\mathbf{A x}+\sum_{i=1}^{m}\mathbf{b}_iu_i\\ y_i&=\mathbf{ c}_i^T\mathbf{ x},\qquad i=1,...,m \end{align}$

定义7.1 向量形式的相对微分度
式(7.1)表示的线性系统会能用有向量表示的 $m$ 个相对微分度 $deg\left\{r_1,...,r_m \right\}$ ，如果满足
① $\mathbf{c}_i^T\mathbf{A}^k\mathbf{b}_j=0,\quad i=1,...,m\quad j=1,...,m\quad k=0,1,...,r_i-2$
②一个 $(m\times m)$ 的矩阵 $\mathbf{H_y}$
(7.2) $\mathbf{H_y}= \begin{bmatrix} \mathbf{c}_1^T\mathbf{A}^{r_1-1}\mathbf{b}_1&\dots&\mathbf{c}_i^T\mathbf{A}^{r_1-1}\mathbf{b}_m\\ \vdots&&\vdots\\ \mathbf{c}_m^T\mathbf{A}^{r_m-1}\mathbf{b}_1&\dots&\mathbf{c}_m^T\mathbf{A}^{r_m-1}\mathbf{b}_m \end{bmatrix}$
是满秩可逆的，即 $rank(\mathbf{H_y})=m$

指数 $r_i$ 的意义是很清楚的，当输出 $y_i=\mathbf{ c}_i^T\mathbf{ x}$ 关于时间连续求导后有

(7.3) $\begin{align} \dot y_i&=\mathbf{ c}_i^T\mathbf{ Ax}~~~~ ~~+\underbrace{\mathbf{ c}_i^T[\mathbf{ b}_1,...,\mathbf{ b}_m]}_{=\mathbf{ 0}~~\because ①}\mathbf{ u} &=&\mathbf{ c}_i^T\mathbf{ Ax}\\ \ddot y_i&=\mathbf{ c}_i^T\mathbf{ A}^2\mathbf{ x}~~~~+\underbrace{\mathbf{ c}_i^T\mathbf{ A}[\mathbf{ b}_1,...,\mathbf{ b}_m]}_{=\mathbf{ 0}~~\because ①}\mathbf{ u} &=&\mathbf{ c}_i^T\mathbf{ A}^2\mathbf{ x}\\ &~~\vdots&~~\vdots&\\ y_i^{(r_i-1)}&=\mathbf{ c}_i^T\mathbf{ A}^{r_i-1}\mathbf{ x}+\underbrace{\mathbf{ c}_i^T\mathbf{ A}^{r_i-2}[\mathbf{ b}_1,...,\mathbf{ b}_m]}_{=\mathbf{ 0}~~\because ①}\mathbf{ u} &=&\mathbf{ c}_i^T\mathbf{ A}^{r_i-1}\mathbf{ x}\\ y_i^{(r_i)}&=\mathbf{ c}_i^T\mathbf{ A}^{r_i}\mathbf{ x}~~~~+\underbrace{\mathbf{ c}_i^T\mathbf{ A}^{r_i-1}[\mathbf{ b}_1,...,\mathbf{ b}_m]}_{\ne\mathbf{ 0}~~\because ②}\mathbf{ u} \end{align}$

我们知道满足这样所有假设①②后，就能得到独立的 $m$ 个相对微分度 $deg\left\{r_1,...,r_m \right\}$ ，它表示从 $m$ 个输入 $u_i$ 开始，各有 $r_i$ 个解耦后的相对的微分度为 $r_i$ 的阶数逐步递增的微分方程。而且输出变量 $y_i$ 必须经历 $r_i$ 次微分以后才会第一次到达输入端，也就是每个控制输入变量 $u_i$ 的直接作用只出现在第 $r_i$ 阶的输出变量上，之后的影响都是间接积分得到。输入量只在入口处出现，跟后面中间过渡量无关，所以输入输出是解耦的。

当所有相对微分度之和的总微分度不超过系统阶数时

(7.4) $r=\sum_{i=1}^{m}{r}_i\leq n$

那么最高阶的输出变量的 $y_i^{(r_i)}$ 就决定了系统的输入输出解耦形式，把(7.3)最后一行表示的写得紧凑一点

(7.5) $\begin{bmatrix} y^{(r_1)}\\\vdots\\y^{(r_m)} \end{bmatrix}=\begin{bmatrix} \mathbf{ c}_1^T\mathbf{ A}^{r_1}\\\vdots\\\mathbf{ c}_m^T\mathbf{ A}^{r_m} \end{bmatrix}\mathbf{ x}+\underbrace{\begin{bmatrix} \mathbf{c}_1^T\mathbf{A}^{r_1-1}\mathbf{b}_1&\dots&\mathbf{c}_i^T\mathbf{A}^{r_1-1}\mathbf{b}_m\\ \vdots&&\vdots\\ \mathbf{c}_m^T\mathbf{A}^{r_m-1}\mathbf{b}_1&\dots&\mathbf{c}_m^T\mathbf{A}^{r_m-1}\mathbf{b}_m \end{bmatrix}}_{\mathbf{H_y}} \underbrace{\begin{bmatrix} u_1\\\vdots\\u_m \end{bmatrix}}_{\mathbf{u}}$

显然SISO系统的微分度只是MIMO系统的相对微分度的一维简化，即 $m=p=1$ 时。定义7.1的简化为

(7.6) $\begin{align} ①&~~~~\mathbf{c}^T\mathbf{A}^k\mathbf{b}=0,\quad k=0,1,...,r_i-2\\ ②&~~~~H_y=\mathbf{c}^T\mathbf{A}^{r-1}\mathbf{b}\ne 0,\quad r\leq n \end{align}$

7.2 输入输出标准型

相对微分度向量 $deg\left\{r_1,...,r_m \right\}$ 能用来确定正则的状态变量变换矩阵

(7.7) $\underbrace{\begin{bmatrix} \mathbf{\tilde x}_y\\\boldsymbol{\eta} \end{bmatrix}}_{\mathbf{\tilde x}} =\underbrace{\begin{bmatrix} \mathbf{T}_y\\\mathbf{T}_{\boldsymbol{\eta}} \end{bmatrix}}_{\mathbf{T}}\mathbf{x}$ , $\mathbf{\tilde x}_y=\begin{bmatrix} \tilde x_{1,1}\\\vdots\\\underline{\tilde x_{1,r_1}}\\\vdots\\\overline{\tilde x_{m,1}}\\\vdots\\\tilde x_{m,r_m} \end{bmatrix}\in \mathbb{R}^r$ , $\mathbf{T}_y=\begin{bmatrix} \mathbf{c}_1^T\\\vdots\\\underline{\mathbf{c}_1^T\mathbf{A}^{r_1-1}}\\\vdots\\\overline{~~~~~\mathbf{c}_m^T~~~~~}\\\vdots\\\mathbf{c}_m^T\mathbf{A}^{r_m-1} \end{bmatrix}\in \mathbb{R}^{r\times n}$

第一个 $r$ 行的状态变量 $\mathbf{\tilde x}_y$ 表示了所有输出变量 $y_i$ 的导数 $y_i^{(j)},j=1,...,r_i-1$ 。如果想使得状态变量的变换矩阵 $\mathbf{T}$ 存在且可逆，必须使剩下的变换矩阵 $\mathbf{T}_{\boldsymbol{\eta}}\in\mathbb{R}^{(n-r)\times n}$ ，所以

(7.8) $rank\begin{bmatrix} \mathbf{T}_y\\\mathbf{T}_{\boldsymbol{\eta}} \end{bmatrix}=n$

所以能导出输入输出标准型的变换定理

定理 7.1 线性输入输出标准型
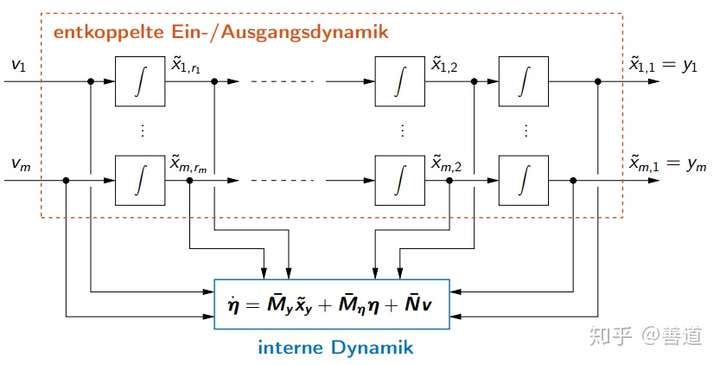
一个式(7.1)决定的线性系统的输出 $\mathbf{y}=[y_1,...,y_m]^T$ 有相对微分度向量 $deg\left\{r_1,...,r_m \right\}$ ，且总的相对微分数 $r=\sum_{i=1}^{m}{r}_i\leq n$ 。那么总可以选出一个变换矩阵 $\mathbf{T}_{\boldsymbol{\eta}}\in\mathbb{R}^{(n-r)\times n}$ 来保证总的变换矩阵 $\mathbf{T}$ 是可逆的，并且系统能够变成输入输出标准型
(7.9)输入输出动态： $\begin{align} \dot{\tilde x}_{i,1}~~~~&=\tilde x_{i,2}\\ &~~\vdots\\ \dot{\tilde x}_{i,r_i-1}&=\tilde x_{i,r_i}\\ \dot{\tilde x}_{i,r_i}~~~~&=\mathbf{g_{y,i}^T}\mathbf{\tilde x}_y+\mathbf{g_{\eta,i}^T}\boldsymbol{\eta}+\mathbf{h_{y,i}^T}\mathbf{u},\qquad i=1,...,m \end{align}$
(7.10)内动态： $\boldsymbol{\dot\eta}~~~~~~~=\mathbf{M_y}\mathbf{\tilde x}_y+\mathbf{M_{\boldsymbol{\eta}}}\boldsymbol{\eta}+\mathbf{Nu}$
其中变换后的输出变量为 $y_i=\tilde x_{i,1}$ , $i=1,...,m$ ，其他矩阵向量分别为
(7.11) $\begin{align} \mathbf{g_{i}^T}&=[\mathbf{g_{y,i}^T}~~\mathbf{g_{\eta,i}^T}]=\mathbf{c}_i^T\mathbf{A}^{r_i}\mathbf{T}^{-1},\qquad &\mathbf{h_{y,i}^T}&=\mathbf{c}_i^T\mathbf{A}^{r_i-1}\mathbf{B}\\ \mathbf{M}~&=[\mathbf{M_{y}}~~\mathbf{M_{\boldsymbol{\eta}}}] =\mathbf{T}_{\boldsymbol{\eta}}\mathbf{A}\mathbf{T}^{-1},\qquad &\mathbf{N}~~~&=\mathbf{T}_{\boldsymbol{\eta}}\mathbf{B} \end{align}$

这合计 $m$ 条对解耦状态变量 $\mathbf{\tilde x}_y\in \mathbb{R}^{r}$ 的积分链，产生了系统输入输出解耦的动态，而剩下的子系统的状态变量 $\boldsymbol{\eta}\in \mathbb{R}^{n-r}$ 就描述了所谓的系统的内动态(interne Dynamik)。在许多情况下，子系统的状态变量 $\boldsymbol{\eta}=[\eta_1,...,\eta_{n-r}]^T$ 也都可以分配给变换前系统唯一对应的状态变量 $x_i$ ，其经由 $\boldsymbol{\eta}=\mathbf{T}_{\boldsymbol{\eta}}\mathbf{x}$ 得到。

7.3 状态解耦和特征值预给

取式(7.5)，它其实就是每个相对微分度下解耦的最后一行

(7.12) $\mathbf{v}=\begin{bmatrix} y^{(r_1)}\\\vdots\\y^{(r_m)} \end{bmatrix}=\begin{bmatrix} \dot{\tilde x}_{1,r_1}\\\vdots\\ \dot{\tilde x}_{m,r_m}\end{bmatrix}=\underbrace{\begin{bmatrix} \mathbf{ c}_1^T\mathbf{ A}^{r_1}\\\vdots\\\mathbf{ c}_m^T\mathbf{ A}^{r_m} \end{bmatrix}\mathbf{T}^{-1}}_{\mathbf{G}}\mathbf{\tilde x} +\underbrace{\begin{bmatrix} \mathbf{ c}_1^T\mathbf{ A}^{r_1-1}\\\vdots\\\mathbf{ c}_m^T\mathbf{ A}^{r_m-1} \end{bmatrix}\mathbf{B}}_{\mathbf{H_y}} \mathbf{u}$

因为基本假设，即耦合矩阵 $\mathbf{H_y}$ 满秩可逆，且存在微分度向量 $deg\left\{r_1,...,r_m \right\}$ 那么原本的输入控制变量 $\mathbf{u}$ 就还可以用新的输入控制量 $\mathbf{v}\in\mathbb{R}^m$ 表示

(7.13) $\mathbf{u}=\mathbf{H_y}^{-1}(\mathbf{v}-\mathbf{G}\mathbf{\tilde x})$

于是导出了输入输出解耦的形式

(7.14) $\begin{align} \dot{\tilde x}_{i,1}~~~~&=\tilde x_{i,2}\\ &~~\vdots\\ \dot{\tilde x}_{i,r_i-1}&=\tilde x_{i,r_i}\\ \dot{\tilde x}_{i,r_i}~~~~&=v_{i},\qquad i=1,...,m \\ \boldsymbol{\dot\eta}~~~~~~~&=\mathbf{\bar M_y}\mathbf{\tilde x}_y+\mathbf{\bar M_{\boldsymbol{\eta}}}\boldsymbol{\eta}+\mathbf{\bar Nv} \end{align}$

其中有(7.15) $\begin{align} \mathbf{\bar M}~&=[\mathbf{\bar M_{y}}~~\mathbf{\bar M_{\boldsymbol{\eta}}}] =\mathbf{M}-\mathbf{N} \mathbf{H_y}^{-1}\mathbf{G},\qquad \mathbf{\bar N}=\mathbf{N} \mathbf{H_y}^{-1}\end{align}$

对于每一条积分链的输出端， $y_i=\tilde x_{i,1}$ 可以借助新的输入端 $\mathbf{v}=[v_1,...,v_m]^T$ 实现既定目标的控制。根据式(7.14)可知，新输入量会对系统的内动态产生影响，而新输入量也可以像之前能控标准型一样，任意配置系统期望的内动态，依据

(7.16) $v_i=-p_{i,0}\tilde x_{i,1}-...-p_{i,r_i-1}\tilde x_{i,r_i},\quad i=1,...,m$

$p_{i,j}$ 依然是目标特征多项式的系数

(7.17) $p^*_i(\lambda)=p_{i,0}+p_{i,1}\lambda+...+p_{i,r_i-1}\lambda^{r_i-1}+\lambda^{r_i}=\prod_{j=1}^{r_i}(\lambda-\lambda^*_{i,j}), ~~i=1,...,m$

然而，与原来单单只用特征值预给可以保证系统的稳定性不同的是，采用输入输出解耦形式时，内动态的稳定性是对整个系统稳定性有决定性的作用。其次，因为实际的输入变量 $\mathbf{u}$ 因为式(7.13)而让内动态状态变量 $\boldsymbol{\eta}$ 实实在在地出现。当内动态是不稳定的时候，也会导致 $\mathbf{v}$ 过高的调控幅值。

如果想要获取内动态的实际稳定性，我们不应该让输入状态以及其他非内动态的状态变量影响它，也就是让内动态变为自治系统，于是我们就需要考察所谓的零动态(Nulldynamik)，先让其他状态变量以及输入量全部置零

$y_i^{(j)}=\tilde x_{i,j+1}=0,~~j=0,1,...,r_i-1\qquad y_i^{(r_i)}=v_i=0,i=1,...,m$

于是由解耦形态直接获得零动态

(7.18) $\boldsymbol{\dot\eta}=\mathbf{\bar M_{\boldsymbol{\eta}}}\boldsymbol{\eta}$

零动态是一种特殊的内动态，当所有输出量都保持零时，它表达了系统最后剩下的动态。只有当零动态是渐进稳定的，整个系统才能保持渐近稳定。

整个经过解耦的输入输出标准型，依然可以利用反馈律进行特征值的配置，利用Ackermann公式和式(7.14)，类似得到

定理7.2 输入输出解耦的状态反馈设计
式(7.1)所示的MIMO线性系统有相对微分度向量 $deg\left\{r_1,...,r_m \right\}$ ，经过输入输出解耦后，得到形如式(7.9)的表达，并且零动态是渐进稳定的。那么会有反馈控制律以及Kalman增益矩阵
(7.19) $\mathbf{K}=\mathbf{H_y}^{-1}\begin{bmatrix} \mathbf{c_1^T}(p_{1,0}\mathbf{I}+p_{1,1}\mathbf{A}+...+p_{1,r_1-1}\mathbf{A}^{r_1-1}+\mathbf{A}^{r_1})\\ \vdots\\\mathbf{c_m^T}(p_{m,0}\mathbf{I}+p_{m,1}\mathbf{A}+...+p_{m,r_m-1}\mathbf{A}^{r_m-1}+\mathbf{A}^{r_m}) \end{bmatrix}$
使系统能够渐近稳定。其中耦合矩阵 $\mathbf{H_y}$ 来自(7.2)，而系数 $p_{i,j}$ 来自特征多项式(7.17)。

解耦的输入输出标准型的Ackermann公式和原本普通的MIMO的标准型不一样，原本Ackermann公式使用变换向量 $\mathbf{t^T}\in\mathbb{R}^n$ 以及耦合矩阵 $\mathbf{H}\in\mathbb{R}^{n\times n}$ ,而输入输出标准型则直接使用输出向量 $\mathbf{c_i^T}\in\mathbb{R}^{n}$ 和新的耦合矩阵 $\mathbf{H_y}\in\mathbb{R}^{m\times m}$ ，有相对微分度向量 $deg\left\{r_1,...,r_m \right\}$ ，且总的相对微分数 $r=\sum_{i=1}^{m}{r}_i<n$ 时，会留出 $n-r$ 阶的系统内动态，只有当系统内动态，或者零动态稳定时，系统才完全稳定。

反馈控制矩阵可以使得输入输出解耦的子系统稳定，整个经由反馈调整后的解耦子系统可如下表示

(7.20) $\begin{bmatrix} \dot{\tilde x}_{i,1}\\\vdots\\\dot{\tilde x}_{i,r_i}\end{bmatrix} =\underbrace{\begin{bmatrix} 0&1&&0\\\vdots&&\ddots\\ 0&0&&1\\ -p_{i,0}&-p_{i,1}&\dots&-p_{i,r_i-1}\end{bmatrix}}_{\mathbf{\tilde A_{y,i}}}\begin{bmatrix} \tilde x_{i,1}\\\vdots\\ \tilde x_{i,r_i}\end{bmatrix},\qquad i=1,...,m$

因充分解耦，可把每个矩阵块 $\mathbf{\tilde A_{y,i}}$ 组成总的解耦子系统矩阵是对角矩阵 $\mathbf{\tilde A_y}=diag(\mathbf{\tilde A_{y,1}},...,\mathbf{\tilde A_{y,m}})$ 。并且考虑内动态系统，会有

(7.21) $\begin{bmatrix} \dot{\mathbf{\tilde x}}_y\\\dot {\boldsymbol{\eta}} \end{bmatrix}=\underbrace{\begin{bmatrix} \mathbf{\tilde A_y}&\mathbf{0}\\\mathbf{\bar M_{\boldsymbol{\eta}}}-\mathbf{\bar NP}&\mathbf{\bar M_{\boldsymbol{\eta}}}\end{bmatrix}}_{\mathbf{\tilde A}_R}\begin{bmatrix} \mathbf{\tilde x}_y\\\boldsymbol{\eta} \end{bmatrix}$

且有(7.22) $\mathbf{P}=\begin{bmatrix}\mathbf{p_1^T}&\mathbf{0}&\dots&\mathbf{0}\\\mathbf{0}&\mathbf{p_2^T}&\dots&\mathbf{0}\\\vdots&&\ddots \\\mathbf{0} &\mathbf{0}& \dots&\mathbf{p_m^T}\end{bmatrix}$ ，它的每一个向量 $\mathbf{p_i^T}=[p_{i,0}~...~p_{i,r_i-1}]$ 都对应了所属特征多项式的系数。因而可求最终合成闭环系统的动态矩阵 $\mathbf{\tilde A}_R$ 的特征值

(7.23) $\det({\lambda\mathbf{I-\tilde A}_R})=\det({\lambda\mathbf{I_{(m)}-\tilde A_y}})\det(\lambda\mathbf{I_{(n-r)}-\bar M_{\boldsymbol{\eta}}})$

闭环系统的特征值正好分别是预给特征多项式和零动态多项式的乘积！也就是说，系统总的特征值是独立分开的，解耦部分用预给特征多项式保证稳定性，内动态用 $\mathbf{\bar M_{\boldsymbol{\eta}}}$ 的特征值保证稳定性。

7.4 系统零动态的含义

借助SISO系统的传递函数，我们会更容易看出系统的零动态行为。

(7.24) $G(s)=\frac{b_0+b_1s+...+b_{n-r}s^{n-r}}{a_0+a_1s+...+a_{n-1}s^{n-1}+s^n}$

显然，上面这个分子分母互质的传递函数的微分度是 $r$ ，它的能控标准型为

(7.25) $\begin{align} \mathbf{\dot x}&=\begin{bmatrix}0&1&&0\\ \vdots&&\ddots\\ 0&0&&1\\ -a_0&-a_1&\dots&-a_{n-1} \end{bmatrix}\mathbf{x}+\begin{bmatrix}0\\\vdots\\0\\1\end{bmatrix}u\\y&=[b_0~~~b_1~~~...~~~b_{n-r}~~~0~~~...~~0]~\mathbf{x} \end{align}$

这个形式也是对传递函数的最小实现。现在把它变成解耦的输入输出标准型，需要借助

(7.26) $\underbrace{\begin{bmatrix} \mathbf{\tilde x}_y\\\boldsymbol{\eta} \end{bmatrix}}_{\mathbf{\tilde x}} =\underbrace{\begin{bmatrix} \mathbf{T}_y\\\mathbf{T}_{\boldsymbol{\eta}} \end{bmatrix}}_{\mathbf{T}}\mathbf{x}$

其中有 $\underbrace{\begin{bmatrix}\tilde x_1\\\vdots\\\tilde x_r\end{bmatrix}}_{\mathbf{\tilde x_y}}=\underbrace{\begin{bmatrix} \mathbf{c^T}\\\mathbf{c^TA}\\\vdots\\\mathbf{c^T}\mathbf{A}^{r-1} \end{bmatrix}}_{\mathbf{T}_y}\mathbf{x}$ , $\underbrace{\begin{bmatrix} \eta_1\\\vdots\\\eta_{n-r}\end{bmatrix}}_{\boldsymbol{\eta} }=\begin{bmatrix}x_1\\\vdots\\x_{n-r}\end{bmatrix}=\mathbf{T_{\boldsymbol{\eta} }x}$

所以解耦的输入输出标准型为

(7.27) $\begin{align} \dot{\tilde x}_{1}~~~&=\tilde x_{2}\\ &~~\vdots\\ \dot{\tilde x}_{r-1}&=\tilde x_{r}\\ \dot{\tilde x}_{r}~~~~&=\mathbf{g_{y}^T}\mathbf{\tilde x}_y+\mathbf{g_{\eta}^T}\boldsymbol{\eta}+H_{y}u\\\boldsymbol{\dot\eta}~~~~~&=\mathbf{M_y}\mathbf{\tilde x}_y+\mathbf{M_{\boldsymbol{\eta}}}\boldsymbol{\eta} \end{align}$

它的内动态的细节有

(7.28) $\begin{align} \dot \eta_1~~~~~~~&=\dot x_1~~~~~~~=x_2~~~~~~~~=\eta_2\\ &\vdots\\ \dot \eta_{n-r-1}&=\dot x_{n-r-1}=x_{n-r}~~~~=\eta_{n-r}\\ \dot \eta_{n-r}~~~&=\dot x_{n-r}~~~~=x_{n-r+1}=-\frac{b_0}{b_{n-r}}\eta_1-...-\frac{b_{n-r-1}}{b_{n-r}}\eta_{n-r}+\frac{1}{b_{n-r}}\tilde x_1\end{align}$

因此内动态的状态方程为

(7.29) $\boldsymbol{\dot\eta}=\underbrace{\begin{bmatrix}0&0&\dots&0\\ \vdots&\vdots&&0\\ 0&0&\dots&0\\ \frac{1}{b_{n-r}}&0&\dots&0\end{bmatrix}}_{\mathbf{\bar M_y}}\mathbf{\tilde x}_y+\underbrace{\begin{bmatrix}0&1&&0\\ \vdots&&\ddots\\0&0&&1\\ -\frac{b_0}{b_{n-r}}&-\frac{b_1}{b_{n-r}}&...&-\frac{b_{n-r-1}}{b_{n-r}}\end{bmatrix}}_{\mathbf{\bar M_{\boldsymbol{\eta}}}}\boldsymbol{\eta}$

令 $\mathbf{\tilde x_y}=\mathbf{0}$ ，于是有零动态 $\boldsymbol{\dot\eta}=\mathbf{\bar M_{\boldsymbol{\eta}}}\boldsymbol{\eta}$ ，求其特征值

(7.30) $\det(\lambda\mathbf{I-\bar M_{\boldsymbol{\eta}}})=-\frac{1}{b_{n-r}}(b_0+b_1\lambda+...+b_{n-r-1}\lambda^{n-r-1}+\lambda^{n-r})$

所以零动态的特征值对应了的传递函数零点！所以只要零动态稳定，其所对应的传递函数的零点就会落在左半平面。当系统是非最小相位的时候，会有一个或者多个传递函数的零点在右半平面，也就是说内动态是不稳定的。所以一个状态反馈控制器在解耦的输入输出标准型下设计的时候，必须要求系统是最小相位的，这样才可以稳定。

这一章我们深入探讨了考虑了系统输出之后应当使输入输出解耦的状态反馈控制器的设计方案，还引入了解耦后出现的系统内动态的概念。下一章要初步讨论最优控制。

善道：线性系统控制入门(八)最优控制——LQR控制器

参考文献：

[1]Regelungstechnik B (Zustandsraummethoden) (WS 2019), Prof. Dr.-Ing. Knut Graichen

Lehrstuhl für Regelungstechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg

现代控制理论线性系统入门(七)输入输出解耦的控制器设计

善道

7.1 相对微分度

7.2 输入输出标准型

7.3 状态解耦和特征值预给

7.4 系统零动态的含义

为你推荐

一知半解|MATLAB机器人建模与仿真控制（4）

单足机器人技术分析——平面单足跳跃机器人

机器人KDL库03-Kinematic Trees

Ensemble Kalman filter集合卡尔曼滤波

【Coppeliasim｜轨迹规划（五）】给机械臂添加手爪

PyBullet (一) 在Ubuntu20.04.1中安装PyBullet（VMware Workstation 16.x Pro）

关于作者

善道

32

0

0

2

德国人怎么学电机——浅谈电机模型(十五)：同步电机(二)凸极电机

学习笔记：数值最优和模型预测控制(三)无约束静态最优化(一)确定步长

德国人怎么学电机——浅谈电机模型(九)：三相交流电机的旋转磁场理论(二)绕组因数

相关推荐

无人驾驶虚拟仿真（十六）--障碍物检测与识别2

鲁棒控制理论（五）Riccati方程控制一阶倒立摆系统

控制算法手记--建模重要嚒？

Bezier曲线构造

优化方法理论合集（12）——动端点问题

【ROS&GAZEBO】多旋翼无人机仿真（四）——探索控制器原理

热门泡泡

30积分失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

现代控制理论线性系统入门(七)输入输出解耦的控制器设计

善道

7.1 相对微分度

7.2 输入输出标准型

7.3 状态解耦和特征值预给

7.4 系统零动态的含义

为你推荐

一知半解|MATLAB机器人建模与仿真控制（4）

单足机器人技术分析——平面单足跳跃机器人

机器人KDL库03-Kinematic Trees

Ensemble Kalman filter集合卡尔曼滤波

【Coppeliasim｜轨迹规划（五）】给机械臂添加手爪

PyBullet (一) 在Ubuntu20.04.1中安装PyBullet（VMware Workstation 16.x Pro）

评论（0）

关于作者

善道

32

0

0

2

德国人怎么学电机——浅谈电机模型(十五)：同步电机(二)凸极电机

学习笔记：数值最优和模型预测控制(三)无约束静态最优化(一)确定步长

德国人怎么学电机——浅谈电机模型(九)：三相交流电机的旋转磁场理论(二)绕组因数

相关推荐

无人驾驶虚拟仿真（十六）--障碍物检测与识别2

鲁棒控制理论（五）Riccati方程控制一阶倒立摆系统

控制算法手记--建模重要嚒？

Bezier曲线构造

优化方法理论合集（12）——动端点问题

【ROS&GAZEBO】多旋翼无人机仿真（四）——探索控制器原理

热门泡泡

30积分 失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分 想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

忘记密码

修改头像

添加你感兴趣的标签

举报类型（必选）

举报详情（选填）

30积分失眠，聊聊自己搞ROS的心得体会吧

5积分想买能用ROS2的开发套件。或者开发板