现代控制理论线性系统入门(六)用能控标准型设计控制器

上一篇传送门：

上一篇初步谈到了如何利用状态变量的反馈来设计状态变量反馈控制器，相比于给定特征值后比较特征多项式系数，实际上还有更加一般方法，即基于能控标准型的设计方法。

6.1 SISO系统的Ackermann公式

第四篇的能控性里面提到过在线性时不变的SISO系统里变成能控标准型的变换

(6.1) $\underbrace{\begin{bmatrix}\tilde x_1\\\vdots\\\tilde x_n\end{bmatrix}}_{\mathbf{\tilde x}}=\underbrace{\begin{bmatrix}\mathbf{ t^T}\\\vdots\\\mathbf{ t^TA}^{n-1}\end{bmatrix}}_{\mathbf{T}}\mathbf{ x},\qquad \mathbf{ t^T}=\left[ 0~~...~~0~~1 \right]\mathbf{ Q}^{-1}_S$

使用能控标准型来设计一个预给系统特征值的控制器是特别适合的，因为控制输入量 $u$ 唯独只会作用到能控标准型的最后一行。能控标准型的紧凑写法是

(6.2) $\begin{align} \dot{\tilde x}_1~~~~&={\tilde x}_2\\ &~~\vdots\\ \dot{\tilde x}_{n-1}&={\tilde x}_n\\ \dot{\tilde x}_n~~~~&=\mathbf{g^T\tilde x}+u\\ \end{align}$ 其中 $\mathbf{g^T}=\mathbf{t^TA^n}\mathbf{T}^{-1}$

如果我们借助特殊的控制律来消除 $\mathbf{g^T\tilde x}$

(6.3) $u=v-\mathbf{g^T\tilde x}$

那么最后合成的状态方程就会是新的输入变量 $v$ 控制下的完全解耦的形式

(6.4) $\begin{align} \dot{\tilde x}_1~~~~&={\tilde x}_2\\ &~~\vdots\\ \dot{\tilde x}_{n-1}&={\tilde x}_n\\ \dot{\tilde x}_n~~~~&=v\\ \end{align}$

这样我们就会得到一条以 $v$ 为输入量，长度为 $n$ 的连续直接积分链，再看看期望的特征值产生的特征多项式

(6.5) $p^*(\lambda)=p_0+p_1\lambda+...+p_{n-1}\lambda^{n-1}+\lambda^n=\prod_{i=1}^{n}(\lambda-\lambda_i^*)$

于是我们只要令新的输入量的控制律如下形式设计，就能实现我们想要的系统性能

(6.6) $v=-p_0{\tilde x}_1-...-p_{n-1}{\tilde x}_{n}$

也就是说合成的闭环系统动态有

(6.7) $\dot {\mathbf{\tilde x}}=\underbrace{\begin{bmatrix}0&1& &0\\ \vdots& &\ddots& \\ 0&0& &1\\ -p_0&-p_1&...&-p_{n-1}\end{bmatrix}}_{\mathbf{\tilde A}_R}\mathbf{\tilde x}$

它的特征多项式是和预期匹配的， $\det{(\lambda\mathbf{I-\tilde A}_R)}=p^*(\lambda)$ 。那么实际的控制变量 $u$ 开始的最初的反馈控制律就变为

(6.8) $\begin{align} u&=-p_0{\tilde x}_1-...-p_{n-1}{\tilde x}_{n}-\mathbf{g^T\tilde x}\\ &=-\underbrace{\mathbf{t^T}(p_0\mathbf{I}+...+p_{n-1}\mathbf{A}^{n-1}+\mathbf{A}^n)}_{\mathbf{k^T}}\mathbf{x} \end{align}$

所以这条用来确定状态反馈Kalman增益 $\mathbf{k^T}$ 的公式即大名鼎鼎的Ackermann公式。

定理6.1 SISO系统下的Ackermann公式
当系统完全能控，就可以使用状态反馈增益向量把系统构成闭环反馈，调节原有系统特征值到任意位置。状态反馈Kalman增益向量的公式为
(6.9) $\mathbf{k^T}=\mathbf{t^T}(p_0\mathbf{I}+...+p_{n-1}\mathbf{A}^{n-1}+\mathbf{A}^n)$
其中 $\mathbf{t^T}$ 是能控矩阵逆矩阵的最后一行，而系数 $p_i$ 是期望特征多项式的对应系数。

例6.1 摩托车动力模型

考察一个摩托车的动力模型的能控性

(6.10) $\mathbf{ \dot x}=\begin{bmatrix}-2.45&-0.98\\ 25.44&-2.67\end{bmatrix}\mathbf{ x}+\begin{bmatrix}0.95\\ 36.32\end{bmatrix}u+\begin{bmatrix}1.0\cdot 10^{-5}\\8.82\cdot 10^{-5} \end{bmatrix}d$

它的能控矩阵为

(6.11) $\mathbf{ Q}_S=\left[ \mathbf{ b},\mathbf{Ab}\right]=\begin{bmatrix}0.95&-38.02\\ 36.32&-72.95\end{bmatrix},\qquad\det(\mathbf{ Q}_S)=1311.81>0$

$\mathbf{ Q}_S$ 可逆，它逆矩阵 $\mathbf{ Q}_S^{-1}$ 的最后一行是 $\mathbf{t^T}=[-0.0277~~0.0007]$ 。原本的动态矩阵 $\mathbf{A}$ 的两个特征值为 $\lambda_{1/2}=-2.562\pm j4.999$ ，这个系统是渐近稳定的，但是振荡也很强烈。所以我们的设计目标是让这个系统的动态能很快且有足够阻尼。

因为系统视为二阶系统，可以设计阻尼 $D^*=\frac{\sqrt{2}}{2}$ ，上升时间 $T^*_{an}=0.2s$ ，算出时间常数 $T^*=Te^{-\frac{\pi}{4}}\approx 0.0912s$ 于是能给出想要的特征值 $\lambda_{1/2}^*=-7.754\pm j7.754$ 。用式(6.9)算出反馈增益 $\mathbf{k^T}=\left[ -1.56~~~0.327 \right]$ ，同时算出静态前置滤波器放大增益 $S=(\mathbf{c^T}(\mathbf{bk^T-A)}^{-1}\mathbf{b})^{-1}=1.063$ 。

令初值为 $\mathbf{x}(0)=\mathbf{x}_0=[0~~~17.2^\circ/s]^T$ ，参考输入信号为 $w=3^\circ/s$ ，得到控制律

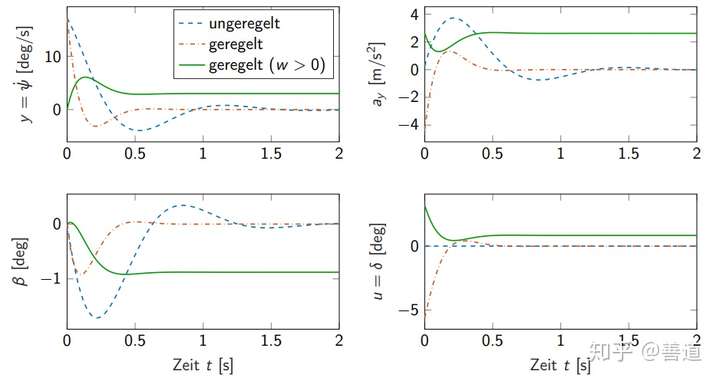
(6.12) $u=-\mathbf{k^Tx}+Sw=-\left[ -1.56~~~0.327 \right]\mathbf{x}+3.189$

下图展示了未反馈控制(蓝色虚线)，仅使用了状态反馈控制(橙色虚线)，同时使用了前置滤波器和状态反馈控制(绿色实线)三种不同情况的时域结果。

6.2 MIMO系统的能控性指数

在MIMO的情况下，系统的状态反馈设计同样能类比SISO情况的能控标准型来实现。首先需要导出MIMO情况下的能控标准型，所以需要先引入能控性指数(Steuerbarkeitsindizes)的概念。为了便于联系，我们先把矩阵 $\mathbf{ B}=\left[ \mathbf{ b_1},...,\mathbf{ b_m} \right]$ 和向量 $\mathbf{ u}=[u_1,...,u_m]^T$ 拆开

(6.13) $\mathbf{\dot x}=\mathbf{ Ax}+\mathbf{ Bu}=\mathbf{ Ax}+\sum_{i=1}^{m}\mathbf{ b}_iu_i,\qquad \mathbf{x}(0)=\mathbf{x}_0$

假设矩阵 $\mathbf{ B}$ 满秩， $rank(\mathbf{ B})=m$ ，那么类似的能控矩阵就可以写成

(6.14) $\mathbf{ Q}_S=[ \mathbf{ b_1},...,\mathbf{ b_m}, \mathbf{ Ab_1},...,\mathbf{ Ab_m}, \mathbf{ A}^{n-1}\mathbf{b_1},...,\mathbf{ A}^{n-1}\mathbf{b_m}]$

如果是SISO情况，我们可以直接使用可逆的 $\mathbf{ Q}_S$ 来求出能控标准型，但是在MIMO里不行，因为MIMO的能控矩阵 $\mathbf{ Q}_S$ 不一定是方阵。然而为了自由配置特征值所需的能控矩阵并不需要所有的 $m\cdot n$ 个列数来控制，事实上就如同SISO系统一样，我们也只需要 $n$ 个线性无关的有效列来控制状态变量。所以我们先找出 $n$ 个线性无关的列向量，这就引出了能控指数。

定义6.1 能控指数
能控指数 $\rho_i$ 指的是，第 $i$ 个式(6.13)所表示的能控系统的指数都是最小的整数，这个最小整数对应的列向量 $\mathbf{ A}^{\rho_i}\mathbf{b}_i$ 都跟式(6.14)左边列的向量线性无关。

当MIMO的能控矩阵可逆时，系统是完全能控的，那么简化的能控矩阵 $\mathbf{ \tilde Q}_S$ 也是完全能控的

(6.15) $\mathbf{ \tilde Q}_S=[ \mathbf{ b}_1,...,\mathbf{ A}^{\rho_1-1}\mathbf{ b}_1,...,\mathbf{ b}_m,..., \mathbf{ A}^{\rho_m-1}\mathbf{b_m}],\qquad \sum_{i=1}^{m}\rho_i=n$

注意！简化的矩阵 $\mathbf{ \tilde Q}_S$ 和原来的 $\mathbf{ Q}_S$ 矩阵元素排列方式不一样。

例6.2 计算能控指数

给定系统

(6.16) $\mathbf{ \dot x}=\begin{bmatrix}0&0&1&0\\ 1&0&2&0\\ 0&1&3&1\\ 0&0&-1&2\end{bmatrix}\mathbf{ x}+\begin{bmatrix}1&0\\0&0\\ 0&0\\ 0&1\end{bmatrix}\mathbf{u}$

其能控矩阵为

(6.17) $\begin{align} &~ \begin{matrix}\mathbf{ b}_1 &\mathbf{ b}_2 &\mathbf{ Ab}_1 &\mathbf{ A b}_2 &\mathbf{ A}^2\mathbf{b}_1 &\mathbf{ A }^2\mathbf{b}_2 &\mathbf{ A}^3\mathbf{b}_1 &\mathbf{ A }^3\mathbf{b}_2 \end{matrix}\\ \mathbf{ Q}_S=& \begin{bmatrix} 1&~0&~ ~~~0&~~~~~~0&~~~~~~~0&~~~~~~~~1&~~~~~~1&~~~~~~~5~~\\ 0&~0& ~~~~1&~~~~~~0&~~~~~~~0&~~~~~~~~2&~~~~~~2&~~~~~~~11~~\\ 0&~0&~~~~0&~~~~~~1&~~~~~~~1&~~~~~~~~5&~~~~~~3&~~~~~20\\ 0&~1&~~~~0&~~~~~~2&~~~~~~~0&~~~~~~~~3&~~~-1&~~~~~1\\ \end{bmatrix} \end{align}$

接下来要找到第一个能控指数 $\rho_1$ 。显然 $\rho_1=1$ 时， $\mathbf{ Ab}_1$ 和 $\mathbf{ b}_1,\mathbf{ b}_2$ 线性无关。这样应有 $\rho_1>1$ 。事实上 $\rho_1=2$ 时，有线性组合 $\mathbf{ A}^2\mathbf{b}_1=\mathbf{ Ab}_2-2\mathbf{ b}_2$ ，类比，得到 $\rho_2=2$ 时，也有线性组合 $\mathbf{ A}^2\mathbf{b}_2=\mathbf{ b}_1+3\mathbf{ b}_2+2\mathbf{ Ab}_1+5\mathbf{ A}^2\mathbf{b}_1$ 。所以能控指数 $\rho_1=\rho_2=2$ ，就会有简化的能控矩阵

(6.18) $\begin{align} &~ \begin{matrix}~\mathbf{ b}_1 &\mathbf{ Ab}_1 &\mathbf{ b}_2 &\mathbf{ A b}_2 \end{matrix}\\ \mathbf{ \tilde Q}_S=& \begin{bmatrix} 1&~~~~0&~ ~~~0&~~~~0&\\ 0&~~~~1& ~~~~0&~~~~0\\ 0&~~~~0&~~~~0&~~~~1\\ 0&~~~~0&~~~~1&~~~~2\\ \end{bmatrix} \end{align}$

6.3 MIMO情况下的能控标准型

能控指数 $\rho_i$ 对于MIMO系统是有根本性意义的，因为借助能控指数简化的能控矩阵就可以把MIMO系统变换到能控标准型。借助变换矩阵

(6.19) $\mathbf{\tilde x}=\mathbf{Tx},\qquad \mathbf{\tilde x}=\begin{bmatrix}\tilde x_{1,1}\\\vdots\\\underline{\tilde x_{1,\rho_1}}\\\vdots\\\overline{\tilde x_{m,1}}\\\vdots\\\tilde x_{m,\rho_m}\end{bmatrix},\qquad\mathbf{T}=\begin{bmatrix}\mathbf{ t_1^T}\\\vdots\\\underline{\mathbf{ t_1^TA}^{\rho_1-1}}\\\vdots\\\overline{~~~~~\mathbf{ t_m^T}~~~~~}\\\vdots\\\mathbf{ t_m^TA}^{\rho_m-1}\end{bmatrix}$

向量 $\mathbf{ t_i^T}$ 需要通过类似的规则从简化的能控矩阵中获得

(6.20) $\begin{bmatrix} \mathbf{ t_1^T}\\\vdots\\\mathbf{ t_m^T} \end{bmatrix}=\begin{bmatrix} \mathbf{ e_1^T}\\\vdots\\\mathbf{ e_m^T} \end{bmatrix}\mathbf{ \tilde Q}_S^{-1},\qquad \mathbf{ e_i^T}=[\underbrace{0,...,0}_{(\sum_{j=1}^{i}{\rho_j})-1},1,0,...,0]\in \mathbb{R}^n$

其中，向量 $\mathbf{ t_i^T}$ 是第 $(\sum_{j=1}^{i}{\rho_j})$ 行的简化能控矩阵的逆矩阵的元素构成的向量。

定理6.2 MIMO系统的能控标准型变换
如果线性MIMO系统满足 $rank(\mathbf{ B})=m$ 且完全能控，能控指数为 $\rho_1,...,\rho_m$ .那么可以把式(6.13)对应的系统变换为能控标准型
(6.21) $\begin{align} \dot{\tilde x}_{i,1}~~~~&={\tilde x}_{i,2}\\ &~~\vdots\\ \dot{\tilde x}_{i,\rho_i-1}&={\tilde x}_{i,\rho_i}\\ \dot{\tilde x}_{i,\rho_i}~~~~&=\mathbf{g_i^T\tilde x}+\mathbf{h_i^Tu},\quad i=1,...,m\\ \end{align}$ 其中 $\begin{align} \mathbf{g_i^T}&=\mathbf{t_i^TA}^{\rho_i}\mathbf{T}^{-1}\\ \mathbf{h_i^T}&=\mathbf{t_i^TA}^{\rho_i}\mathbf{B} \end{align}$
向量 $\mathbf{ t_i^T}$ 是第 $(\sum_{j=1}^{i}{\rho_j})$ 行的简化能控矩阵的逆矩阵的元素构成的向量。

那么矩阵表示的能控标准型形式为

(6.22) $\dot {\mathbf{\tilde x}}=\underbrace{ \begin{bmatrix} \mathbf{\tilde D}_1&\mathbf{\tilde N}_1^2&\dots&\mathbf{\tilde N}_1^m\\ \mathbf{\tilde N}_2^1&\mathbf{\tilde D}_2&\dots&\mathbf{\tilde N}_2^m\\ \vdots&\vdots&\ddots&\vdots\\ \mathbf{\tilde N}_m^1&\mathbf{\tilde N}_m^2&\dots&\mathbf{\tilde D}_m\\ \end{bmatrix} }_{\mathbf{\tilde A}=\mathbf{TAT}^{-1}}\mathbf{\tilde x}+\underbrace{ \begin{bmatrix} \mathbf{\tilde B}_1\\ \mathbf{\tilde B}_2\\ \vdots\\ \mathbf{\tilde B}_m\\ \end{bmatrix} }_{\mathbf{\tilde B}=\mathbf{TB}}\mathbf{u}$

其中矩阵块为

(6.23) $\mathbf{ \tilde D}_i=\begin{bmatrix}0&1& &0\\ \vdots&&\ddots\\0&0&&1\\ \times&\times&\dots&\times\\ \end{bmatrix}\in \mathbb{R}^{\rho_i\times \rho_i},\qquad \mathbf{ \tilde N}_i^j=\begin{bmatrix}0&\dots&0\\ \vdots&&\vdots\\ 0&\dots&0\\\times&\dots&\times\\ \end{bmatrix}\in \mathbb{R}^{\rho_i\times \rho_j}$

(6.24) $\mathbf{ \tilde B}_i=\begin{bmatrix}0&\dots&0&0&0&\dots&0\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\ 0&\dots&0&0&0&\dots&0\\ \times&\dots&\times&1&\times&\dots&\times\\ \end{bmatrix}\in \mathbb{R}^{\rho_i\times m}$

符号" $\times$ "表示一个不一定为0或1的组成元素。总的来说，在 $(m>1)$ 的MIMO的情况下就是有 $m$ 个方块对应的 $\rho_i$ 维的状态变量 $(\tilde x_{i,1},...,\tilde x_{i,\rho_i})$ 分别构成了一组状态方程。

例6.3 计算能控标准型

继续考察前面例6.2的简化过的能控矩阵的逆矩阵

(6.25) $\mathbf{ \tilde Q}_S^{-1}=\begin{bmatrix} 1&0&0&0\\ 0&1& 0&0\\ 0&0&2&1\\ 0&0&1&0\\ \end{bmatrix}$

能控指数 $\rho_1=\rho_2=2$ 所以 $\mathbf{ t_1^T}$ ， $\mathbf{ t_2^T}$ 分别为逆矩阵第二行和第四行的元素

(6.26) $\mathbf{ t_1^T}=[0 ~~1~~0~~0],\quad \mathbf{ t_2^T}=[0 ~~0~~1~~0]$

(6.27) $\mathbf{\tilde x}=\begin{bmatrix} \tilde x_{1,1}\\\tilde x_{1,2}\\\tilde x_{2,1}\\\tilde x_{2,2} \end{bmatrix}=\mathbf{Tx},\quad \mathbf{T}=\begin{bmatrix}\mathbf{ t_1^T}\\\mathbf{ t_1^TA}\\\mathbf{ t_2^T}\\\mathbf{ t_2^TA}\end{bmatrix}=\begin{bmatrix} 0&1&0&0\\ 1&0& 2&0\\ 0&0&1&1\\ 0&1&3&1\\ \end{bmatrix}$

最后经过计算，得到标准型的矩阵表达

(6.28) $\mathbf{ \dot x}=\begin{bmatrix} 0&0&1&0\\ 0&0&1&2\\ 0&0&0&1\\ -2&1&-7&5\end{bmatrix}\mathbf{ x}+\begin{bmatrix}0&0\\1&0\\ 0&0\\ 0&1\end{bmatrix}\mathbf{u}$

6.4 MIMO系统的状态变量解耦和预给特征值

类似SISO系统，在MIMO系统也有线性的状态反馈的控制律可以设计

(6.29) $\mathbf{u}=-\mathbf{Kx}+\mathbf{Sw}$

然后再预给特征值，配置系统性能。所以在能控标准型时设计是特别有优势的，因为控制输入量每每都在单个积分链的末端进入，或者说是在每个矩阵块 $\mathbf{ \tilde B}_i$ 的最后一行出现。我们同样可以利用MIMO系统能控标准型的解耦形式来设计反馈控制律。

能控标准型的微分方程的最后一行，也可以放在一起这样表达

(6.30) $\begin{bmatrix}\dot{\tilde x}_{1,\rho_1}\\\vdots\\\dot{\tilde x}_{m,\rho_m} \end{bmatrix} =\begin{bmatrix}\mathbf{ t_1^TA}^{\rho_1} \\\vdots\\\mathbf{ t_m^TA}^{\rho_m} \end{bmatrix}\mathbf{T}^{-1} \mathbf{ \tilde x} +\underbrace{\begin{bmatrix}\mathbf{ t_1^TA}^{\rho_1-1} \\\vdots\\\mathbf{ t_m^TA}^{\rho_m-1}\end{bmatrix}\mathbf{B} }_{\mathbf{H}}\mathbf{ u}$

假设有 $rank(\mathbf{ B})=m$ ，那么耦合矩阵 $\mathbf{H}\in \mathbb{R}^{m\times m}$ 可逆，于是反推出输入控制量为

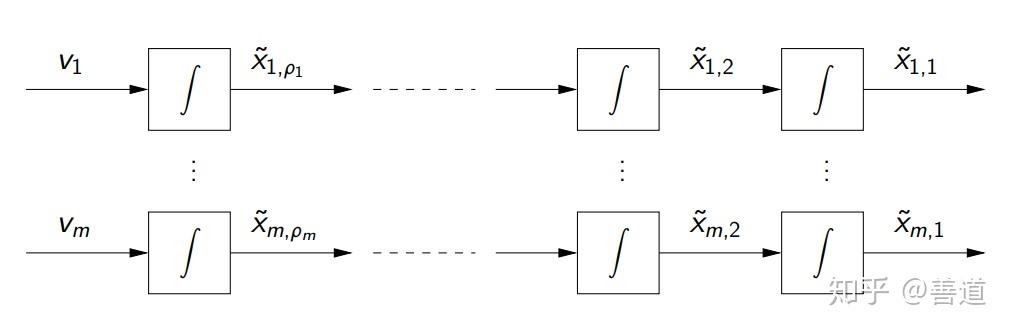
(6.31) $\mathbf{ u}=\mathbf{ H}^{-1}\left( \mathbf{ v} -\begin{bmatrix}\mathbf{ t_1^TA}^{\rho_1} \\\vdots\\\mathbf{ t_m^TA}^{\rho_m} \end{bmatrix}\mathbf{T}^{-1} \mathbf{ \tilde x} \right)$

于是就有了新的输入变量 $\mathbf{v}=[v_1,...,v_m]^T$ 使得原有的能控标准型各个状态变量之间完全解耦，并且能得到总共 $m$ 条积分链，如图6.3所示。于是就可以和SISO系统里一样，设计 $\mathbf{v}$ 满足预给特征值产生的特征多项式。

(6.32) $v_i=-p_{i,0}\tilde x_{i,1}-...-p_{i,\rho_i-1}\tilde x_{i,\rho_i},\qquad i=1,...,m$

其中 $p_{i,j}$ 为期望特征多项式的系数

(6.33) $p^*_i(\lambda)=p_{i,0}+p_{i,1}\lambda+...+p_{i,\rho_i-1}\lambda^{\rho_i-1}+\lambda^{\rho_i}=\prod_{j=1}^{\rho_i}(\lambda-\lambda_{i,j}^*)$

其中第 $i$ 个矩阵块对应的完全解耦的状态方程为(总共 $m$ 个)

(6.34) $\begin{bmatrix}\dot{\tilde x}_{i,1}\\\vdots\\\dot{\tilde x}_{i,\rho_i} \end{bmatrix} =\underbrace{\begin{bmatrix}0&1& &0\\ \vdots& &\ddots& \\ 0&0& &1\\ -p_{i,0}&-p_{i,1}&...&-p_{i,\rho_i-1}\end{bmatrix}}_{\mathbf{\tilde A}_{R,i}}\begin{bmatrix}\tilde x_{i,1}\\\vdots\\ \tilde x_{i,\rho_i} \end{bmatrix}$

其中 $\det(\lambda\mathbf{I-\tilde A}_{R,i})=p^*_i(\lambda)$ 。实际的输入控制律即

(6.35) $\mathbf{ u}=-\underbrace{\mathbf{ H}^{-1}\left( \begin{bmatrix}p_{1,0}\mathbf{t_1^T}+...+p_{1,\rho_1-1}\mathbf{t_1^TA}^{\rho_1-1} \\\vdots\\p_{m,0}\mathbf{t_m^T}+...+p_{m,\rho_1-1}\mathbf{t_m^TA}^{\rho_m-1} \end{bmatrix}+\begin{bmatrix}\mathbf{ t_1^TA}^{\rho_1} \\\vdots\\\mathbf{ t_m^TA}^{\rho_m} \end{bmatrix} \right) }_{\mathbf{ K}}\mathbf{ x}$

这里就包含了MIMO的Ackermann公式。

定理3.3 MIMO系统下的Ackermann公式
如果式(6.13)对应的MIMO系统的控制矩阵 $rank(\mathbf{ B})=m$ ，且完全能控，那么经过状态反馈的动态矩阵 $\mathbf{A}_R=\mathbf{A-BK}$ 是可以任意配置特征值的，用于反馈的Kalman增益 $\mathbf{K}$ 为
(6.36) $\mathbf{K}=\mathbf{ H}^{-1}\begin{bmatrix}\mathbf{t_1^T}(p_{1,0}\mathbf{I}+p_{1,1}\mathbf{A}+...+p_{1,\rho_1-1}\mathbf{A}^{\rho_1-1}+ \mathbf{A}^{\rho_1} )\\\vdots\\\mathbf{t_m^T}(p_{m,0}\mathbf{I}+p_{m,1}\mathbf{A}+...+p_{m,\rho_1-1}\mathbf{A}^{\rho_m-1} +\mathbf{ A}^{\rho_m})\end{bmatrix}$
耦合矩阵 $\mathbf{H}$ 由式(6.30)给出，而向量 $\mathbf{ t_i^T}$ 则是由简化能控矩阵的逆矩阵的第 $(\sum_{j=1}^{i}{\rho_j})$ 行的元素组成。而系数 $p_{i,j}$ 为期望的预给特征多项式的系数。

在MIMO系统里会享有，在SISO系统中不存在的，许多不同的自由度，比如预给特征值的时候，这 $m$ 个特征多项式的选择是不唯一的，而这合计 $n$ 个特征值 $\left\{ \lambda_{1,1}^* ,...,\lambda_{1,\rho_1}^*\right\}$ ..... $\left\{ \lambda_{m,1}^* ,...,\lambda_{m,\rho_m}^*\right\}$ 怎么分配到对应的特定的能控指数下。此外原则上，只要能够让简化的能控矩阵 $\mathbf{ \tilde Q}_S$ 满秩，还有很多不同的能控指数的组合 $\left\{ \rho_1^{'},...,\rho_m^{'}\right\}$ 。

例6.4 计算反馈Kalman增益

继续拓展设计来自例6.3里的系统，其中已经求得

能控指数 $\rho_1=\rho_2=2$ ， $\mathbf{ t_1^T}=[0 ~~1~~0~~0],\quad \mathbf{ t_2^T}=[0 ~~0~~1~~0]$

耦合矩阵为 $\mathbf{ H}=\begin{bmatrix}\mathbf{ t_1^TA}\\\mathbf{ t_2^TA}\end{bmatrix}\mathbf{ B}=\begin{bmatrix}1&0\\0&1\end{bmatrix}$ 所以其逆矩阵 $\mathbf{ H}^{-1}=\mathbf{ I}$ ，原本的动态矩阵 $\mathbf{ A}$ 的特征值为 $\lambda_{1/2}=-0.2806\pm j0.419$ , $\lambda_{3/4}=2.7806\pm j0.367$ ，系统是不稳定的。现在选定期望的特征值移动到 $\left\{ -1~~-1~~-2~~-2 \right\}$ 。这样两组特征值还可以自由分配，比如选出两对特征值

$\begin{align} \left\{ \lambda_{1,1}^*,\lambda_{1,2}^* \right\}&=\left\{ -1,-1\right\}\\ \left\{ \lambda_{2,1}^*,\lambda_{2,2}^* \right\}&=\left\{ -2,-2\right\} \end{align}$ $\Rightarrow \quad \mathbf{ K}=\begin{bmatrix}2&3&11&2\\ 1&7&26&9 \end{bmatrix}$

抑或是另一种选法

$\begin{align} \left\{ \lambda_{1,1}^*,\lambda_{1,2}^* \right\}&=\left\{ -1,-2\right\}\\ \left\{ \lambda_{2,1}^*,\lambda_{2,2}^* \right\}&=\left\{ -1,-2\right\} \end{align}$ $\Rightarrow \quad \mathbf{ K}=\begin{bmatrix}3&4&13&2\\ 1&5&21&8 \end{bmatrix}$

这一章我们探讨了借助能控标准型设计系统状态反馈的Kalman增益，不过却完全没有考虑输出变量在系统坐标变换后的受到的影响，因为系统的耦合，最终输出不一定如我们所愿。下一章要继续探讨输入输出解耦的状态反馈控制器的设计。

下一章传送门：

善道：线性系统控制入门(七)输入输出解耦的控制器设计

参考文献：

[1]Regelungstechnik B (Zustandsraummethoden) (WS 2019), Prof. Dr.-Ing. Knut Graichen

Lehrstuhl für Regelungstechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg

现代控制理论线性系统入门(六)用能控标准型设计控制器

善道

6.1 SISO系统的Ackermann公式

6.2 MIMO系统的能控性指数

6.3 MIMO情况下的能控标准型

6.4 MIMO系统的状态变量解耦和预给特征值

为你推荐

仿生足式机器人与SLIP模型1:奔跑运动的仿生特征

Adams与Matlab的机器人联合仿真【附源文件】

无人机仿真代码更新（如果您想要为此分支创建跟踪信息，您可以执行： git branch --set-upstream-to=origin/<分支> master）

机器人仿真平台V-REP学习入门

卡尔曼估计两步法

精选MATLAB以符号形式表示门函数的傅里叶正反变换。

关于作者

善道

32

0

0

2

德国人怎么学电机——浅谈电机模型(十五)：同步电机(二)凸极电机

现代控制理论线性系统入门(七)输入输出解耦的控制器设计

德国人怎么学电机——浅谈电机模型(二)：直流电机(一)机械构造和基本原理

相关推荐

论文阅读笔记《Learning Deep Network for Detecting 3D Object Keypoints and 6D Poses》

变分与拉格朗日量(2):从欧拉-拉格朗日方程到薛定谔方程

Power PMAC运动控制器 —— 学习笔记1

matlb：kmeans命令进行聚类和pdist2进行预测(含代码)

振动筛分机械动力学分析

现代控制理论线性系统入门(十)轨迹追踪反馈控制

热门泡泡

30积分失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

现代控制理论线性系统入门(六)用能控标准型设计控制器

善道

6.1 SISO系统的Ackermann公式

6.2 MIMO系统的能控性指数

6.3 MIMO情况下的能控标准型

6.4 MIMO系统的状态变量解耦和预给特征值

为你推荐

仿生足式机器人与SLIP模型1:奔跑运动的仿生特征

Adams与Matlab的机器人联合仿真【附源文件】

无人机仿真代码更新（如果您想要为此分支创建跟踪信息，您可以执行： git branch --set-upstream-to=origin/<分支> master）

机器人仿真平台V-REP学习入门

卡尔曼估计两步法

精选MATLAB以符号形式表示门函数的傅里叶正反变换。

评论（0）

关于作者

善道

32

0

0

2

德国人怎么学电机——浅谈电机模型(十五)：同步电机(二)凸极电机

现代控制理论线性系统入门(七)输入输出解耦的控制器设计

德国人怎么学电机——浅谈电机模型(二)：直流电机(一)机械构造和基本原理

相关推荐

论文阅读笔记《Learning Deep Network for Detecting 3D Object Keypoints and 6D Poses》

变分与拉格朗日量(2):从欧拉-拉格朗日方程到薛定谔方程

Power PMAC运动控制器 —— 学习笔记1

matlb：kmeans命令进行聚类和pdist2进行预测(含代码)

振动筛分机械动力学分析

现代控制理论线性系统入门(十)轨迹追踪反馈控制

热门泡泡

30积分 失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分 想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

忘记密码

修改头像

添加你感兴趣的标签

举报类型（必选）

举报详情（选填）

30积分失眠，聊聊自己搞ROS的心得体会吧

5积分想买能用ROS2的开发套件。或者开发板