【ROS&GAZEBO】多旋翼无人机仿真（一）——搭建仿真环境
【ROS&GAZEBO】多旋翼无人机仿真（二）——基于rotors的仿真
【ROS&GAZEBO】多旋翼无人机仿真（三）——自定义多旋翼模型
【ROS&GAZEBO】多旋翼无人机仿真（四）——探索控制器原理
【ROS&GAZEBO】多旋翼无人机仿真（五）——位置控制器
【ROS&GAZEBO】多旋翼无人机仿真（六）——SE(3)几何姿态控制器
【ROS&GAZEBO】多旋翼无人机仿真（七）——四元数姿态控制
【ROS&GAZEBO】多旋翼无人机仿真（八）——手把手编写四元数姿态控制器

为什么需要四元数
从直观来看，欧拉角或者姿态角是最直观的能感受到三维旋转的表示方法。因此，在做多旋翼或者其他机器人的姿态控制时，最能够直观接受的方法就是欧拉角姿态控制。可能很多人会觉得，为什么需要那么多花里胡哨的方法呢，控制俯仰-滚转-航向三个姿态角就能够稳定姿态了。但是，用姿态角进行控制是有前提的，那就是小角度假设，如果不满足小角度的条件，那么姿态角控制就不适用。姿态角是存在旋转顺序的，并且存在万向节死锁，具体可以看上一篇【ROS&GAZEBO】多旋翼无人机仿真（六）——SE(3)几何姿态控制器

四元数表示
因此，我们想要一种参数少，并且不存在旋转顺序和死锁的姿态描述方法。因此，四元数表示法就被提出来了，四元数通常表示形式是这样的：
q = [ q 0 q 1 q 2 q 3 ]

采用轴角方式表达如下：
q=[cos2α​usin2α​​]

它对应于绕一个向量v = ( v x , v y , v z ) 为轴旋转θ \thetaθ的操作（右手法则的旋转）：

q=cos2/θ​+isin2/θ​+jsin2/θ​+ksin2/θ​

四元数旋转
我们知道，姿态矩阵左乘向量即可得到旋转后的向量，四元数同样也可以对向量进行旋转，四元数对三维向量的旋转公式如下：
v ′ = q v q ∗ 

其中v 为纯四元数：

v=[0v​]

v就是三维向量，实部为0，这个公式也是四元数旋转中用得最广泛的一个公式。本篇讲的是如何做四元数误差控制，因此证明过程这里不做讲解

有了这个公式，我们就可以定义四元数的连续旋转。我们来看下面的情况。首先对v 1 进行旋转，这里旋转的四元数是q1
​    
 
v 1 ′ = q 1 v 1 q 1 ∗

接着用q 2 对v 1 进行旋转：
v ′ ′ = q 2 v ′ q 2 ∗ 可以发现，这里的v ′ ′ \mathbf v''v 
′′
 是v 1 经过了两次旋转得到的结果，那v ′ ′ 和v 1 的关系是什么样的呢？下面的式子很明显成立
v ′ ′ = q 2 ( q 1 v q 1 ∗ ) q 2 ∗

然后根据单位四元数共轭的性质：
q ∗ = q − 1 可得
v ′ ′ = ( q 2 q 1 ) v ( q 2 q 1 ) ∗ 因此，q 2 q 1 是这两次旋转复合的四元数。也说明了四元数乘法在几何上的意义就是连续的旋转。好了，有了这个性质，我们就可以去计算四元数的姿态误差了。我们来看下面这个图，这个图表示的就是连续旋转两次的意思。

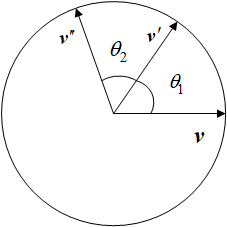
那如果我们把θ 2 换一下，用Δ θ 来表示，v 表示初始水平姿态的向量，v s 表示当前姿态的向量，v d

表示期望姿态的向量。那么连续旋转公式变为：
q d = Δ q ⋅ q s 

​    
 

Δ q 表示的是旋转Δ θ

对应的四元数，q d 表示旋转θ d 对应的四元数，用图来表示如下：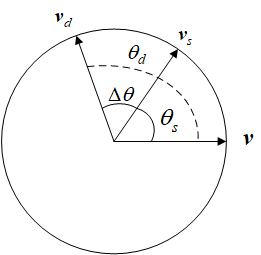

Δq很明显，就是从当前的姿态到期望姿态的误差。那如何得到Δ q 呢？很明显，这不能直接通过减法得到，将上面的式中进行变换：
qd​⋅(qs​)−1=Δq⋅qs​⋅(qs​)−1

Δq=qd​⋅(qs​)−1​

终于大功告成，误差四元数计算公式就有了。然后怎么得到各轴误差角度呢？假设期望和当前的误差角很小，那么下式中的s i n θ sin\thetasinθ和θ \thetaθ就可以替换：

q=cos2/θ​+isin2/θ​+jsin2/θ​+ksin2/θ​

因此，得到的误差四元数的虚部就是各轴的姿态误差分量，但是还忽略了一个重要的问题，那就是同样的旋转，四元数并不是唯一的，可以通过图来直观的理解一下：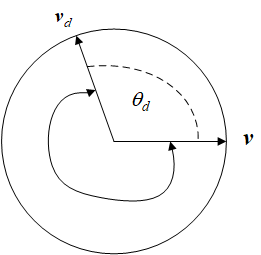

从v 到v d除了虚线表示的θ d 之外，2 π − θ d 很显然也可以达到同样的旋转，这其中就有一个最短旋转角度的问题，但是这两个旋转是有关系的，即2 π − θ d的四元数为− q 。所以，假想一下，飞机从15度回到0度有两种方式，一种是绕轴旋转15度，还有一种是绕轴旋转365度，程序算出来说，哎，我就是玩，我不直接用最小的角度回去，我要绕轴旋转365度回去，，，，好像从原理上来说没毛病，没有错，都可以回到0度，但是实际上没人也不会有人用后面这种方式去这样做吧。。除了谁有十年的脑血栓。

回到正题，我们得到误差的时候也需要去回避这个问题，那怎么去回避呢，上面说过了，− q -\mathbf q−q旋转的角度为2 π − θ d 2\mathrm\pi-\theta_d2π−θ 
d
​    
 ，那就好办了，q的实部q 0 是c o s θ 2 cos\frac\theta2cos 
2
θ
​    
 ，而c o s θ /2 只有在[ − π , π ] 上为正，超过这个范围就为负，那可不可以根据q 0 来判断旋转角是不是最小的呢，答案很明显是的。

因此，只要判断q 0 的正负，就可以判断误差四元数是不是最小的旋转角，如果不是，我们将四元数取反，那最终根据四元数求得到的各轴误差角度分量，误差角度也就是期望的角速度，计算公式就可以整理出来了：
ωd​=ksgn(qerr,0​)qerr,1:3​qerr​=qd​⋅qs​−1​
​    
 

k 是可调节的误差系数，因为是近似的，所以k 可以用来调节误差得到期望角速度的大小。需要注意的是，这里面的乘法是四元数乘法，并且四元数都是单位四元数。

好了，关于四元数姿态控制的内容就讲到这里，下一篇，将介绍如何将四元数控制方法用在四旋翼的仿真中。

最后再讲两句，鄙人也在深入研究四元数、李群和李代数这部分的内容，也深刻体会到四元数误差的推导过程可能会有一点抽象，因为四元数是四维空间的变量，所以并不能很直观的理解，这里需要小伙伴去深入琢磨。此外，四元数是复数的扩展，可能有的小伙伴会说，我连复数都没玩明白，复数其实就可以表示旋转，只不过是2维的旋转，四元数是3维的旋转，因此，复数和四元数有许多相似的性质，讲到这里，是不是感觉有些奇妙和不可思议，这就是数理美妙的所在。欢迎感兴趣的小伙伴添加微信 Reed_UAV 进行交流：