上一篇文章我们介绍了MIMO系统在状态空间方程中的标准型转化问题。不过上一节我并没有给出例子，也没有讲状态反馈的问题。MIMO也可以像SISO系统那样有全状态反馈，不过会出现一些MIMO独特的问题。这篇的重点放在MIMO系统的状态反馈解耦上面，以及解释一下什么是Brunovsky Canonical Form。

MIMO系统的解耦历史上出现过很多方法，这里我们简单介绍下Morgan's Problem，然后主要关注状态反馈解耦的方法。还有其他解耦的方法以后有机会再提，比如现代频域法里面的Inverse Nyquist Array，不过有些方法太繁琐了，有更好的解决办法就用更先进的。

本篇目录：

1. 解耦与Morgan's Problem / Decoupling and Morgan's Problem

2. Brunovsky标准型: case of SISO / Brunovsky Canonical Form of SISO

3. MIMO标准型与极点配置 Brunovsky Canonical Form and Pole Placement

4.MIMO输入输出-状态反馈解耦 Decoupling of MIMO system via state feedback

1. 解耦与Morgan's Problem / Decoupling and Morgan's Problem

1.1 耦合与解耦 coupling and decoupling

MIMO系统的解耦(decoupling)问题由来已久了。首先，什么是耦合（coupling）呢？不管是书上还是讨论，总出现这个词。耦合，就是相互作用的意思。两个量耦合了，就是说这两个量相互之间存在关联，其中一个变化了，另外一个也变化了。那么所谓的解耦，就是想通过某种手段，能够等效地把这个两个量给分开。当然实际中可能不止两个量耦合了，解耦的目的就是想分开这些量，希望它们不要相互作用。

那么MIMO系统耦合发生在哪里呢？ MIMO系统拥有多个输出。在SISO系统中由于输出矩阵  只有一行，所以SISO的输出无非就是多个状态的一种线性组合（linear system only, 非线性的话也是某种非线性组合）。MIMO的输出矩阵就不止一行了，而是有几个输出就有几行，不同的输出都是由状态变量构成的。如果现在系统有两个输入，我们可以改变其中一个输入  使得某一个输出  发生变化。但是因为系统内部的状态之间是互相影响的，即动态是耦合的，所以  可能会导致全部或者部分状态变量发生了改变。而另外一个输出  可能就是由这些被  影响了的状态变量构成，因此在外部看来也发生了改变。如果能够设计一个方法使得MIMO系统的输出不再相互影响，让一个输入对应一个输出，那么就能把MIMO系统等效地看作是多个SISO系统，每一个SISO系统都可以单独地设计反馈控制律，这就非常nice。

解决上述问题，要解答两个问题：系统能够被解耦的充分必要条件，以及确定解耦控制律和系统结构。

1.2 摩根问题 Morgan's Problem

Morgan's Prolem是来源于Bernard. S. Mrorgan首次提出的状态反馈MIMO解耦问题，后来其他研究者就以他的名字来命名这个问题。历史上这个问题分为了两个阶段，开始的时候大家研究当输入数  和输出数  相等时系统能够完全解耦的条件，即  （方形系统的解耦），后来就变成了  情况的研究。后来的Morgan's Problem多指的是non-squared decoupling(非方系统的解耦), 即第二种情况。

1964年，Bernard S. Morgan Jr. 在[1]中首次提出了用static state feedback实现multivariable system解耦。在此之前频域解耦方法已经被研究出来了，但是比较繁琐。(研究者都不是一般的高手)。解耦的系统也叫noninteracting system，即无关联作用的系统。 他希望设计static feedback：

来实现让  维LTI系统的  维input和  维output一一对应，在[1]中得到的只是一个sufficient condition。

3年之后, Falb和Wolovich在[2]中发表了static state feedback解耦的sufficient and necessary condition，只要确定一个非常容易构造的矩阵(原文叫矩阵  )的可逆性就能判断其是否可以被static state feedback解耦（注意是静态的，说的是用(1)）。这个结论就被写在了刘豹的《现代控制理论》第三版的第206页上，作为系统状态反馈解耦的充要条件。

在其他学者的共同努力下(我觉得主要是数学家的功劳), E. G. Gilbert于1969年在[3]中比较系统整理了Morgan's Problem，并且考虑了反馈律(1)。他给出了system is decoupled的定义：使用(1)为反馈的闭环系统传递函数矩阵是对角矩阵，则系统是解耦的。他还指出如果开环系统  的传递函数的行列式为0，则可以推出矩阵E的行列式  ，这种情况称系统有strong inherent coupling，没有任何反馈律能够解耦系统；如果  则系统可以由(1)形式的static feedback解耦，it has no inherent coupling；如果  ，而开环系统  的开环传递函数行列式不为0，则(1)虽然不能解耦，但是还存在其他反馈律可以解耦(那就意味着可以由动态反馈律解耦），有weak inherent coupling。实际上[4]已经证明了“几乎所有”triple  都是可以解耦的，此时还是输入等于输出的情况。这个几乎所有，是有语境的，也就是说存在满足一定条件的triple确实不行，但言下之意绝大多数方形系统都是能够解耦的。

而后的非方系统的解耦问题就难太多了，可以参考[5]了解一下解耦控制的发展路程。距离[5]都19年了，实际上线性系统的Morgan's Problem都没有得到完全解决。

作为入门知识学习，我们就先看  的情况就行了，并且这里只关心状态反馈。频域方法以后再说。

2. Brunovsky标准型: case of SISO / Brunovsky Canonical Form of SISO

上一篇文章中我们留下一个问题，其实之前得到的MIMO标准型还不完全是Brunovsky Canonical Form，还差那么一点，而且我也没有给出例子。在揭开答案之前，我们先给出一个定义：

定义[Static linear feedback equivalence]: 两个系统  是static linear feedback equivalence的，如果存在两个可逆矩阵  和一个矩阵  使得 

两个线性系统  和  如果可以通过线性变换，静态状态反馈和前馈补偿相互转化，那么它们就是静态反馈等价的[6,p90]。等价关系是自反且可传递的，不用多说。我们来看SISO的例子：

对于一个能控的SISO系统 ，我们显然能够把它变成一个能控标准型：

其等效的微分方程就变成了：

这时候采用一个控制律：

把  当作新系统，就可以得到一个纯串联积分系统：

其状态空间方程矩阵为：

由此可见  总是可以通过线性变换，再加上状态反馈和前馈(v)变成(6)，我们把(6)写成状态方程就是：  。

事实证明这里的  就是我们第10篇文章中的  ，所以我们有  的第一行：

其中  为能控性矩阵。然后完整的  定义为：

 则可以找到为：  ，  。

我们说任何一个能控的SISO LTI系统  都能够通过  等价于标准型  。矩阵形同(6)的标准型(F,G)就叫做Brunovsky Canonical Form。

3. MIMO标准型与极点配置 Canonical Form and Pole Placement

那么看完，我们就知道其实上一篇中的MIMO标准型，即所谓的Luenberger第二标准型，还不完全是Brunovsky Canonical Form。我们现在来演示下如何把MIMO系统转化为Brunovsky Form，考虑一个MIMO系统（全是随机生成的）：

可以看到这是一个能控的5维系统，且  的维度是3，我们有3个独立输入。现在令  的每一列为  ，我们开始挑选线性无关列，开始检查  是否和之前的所有列线性无关。我们用MATLAB可以检查它们组成的秩是否增加，如果秩和列的数目一样则保留，否则就可以停止了。

从以上结果我们就可以看出，我们5个线性无关项已经找到了，  矩阵构成为：

能控性指数为  。计算  ，采用上一篇文章中的矩阵(10)，  我们得到：

那么我们就能得到MIMO标准型，也是Luenberger第二标准型（详见我上一篇文章吧）：

以下是两个例子，一个是5维系统，一个是4维系统，独立输入分别是3与2。

A=round(rand(5,5)*10)
B=round(rand(5,3)*10)
rank(ctrb(A,B))
P=[B(:,1),A*B(:,1),B(:,2),A*B(:,2),B(:,3)]
Pinv=inv(P)
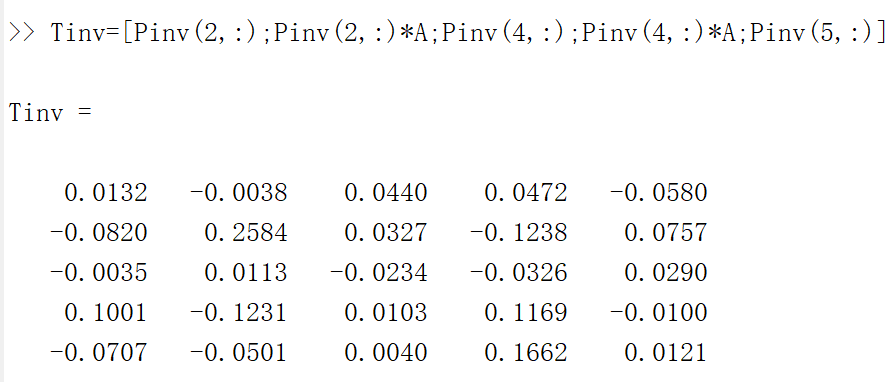
Tinv=[Pinv(2,:);Pinv(2,:)*A;Pinv(4,:);Pinv(4,:)*A;Pinv(5,:)]
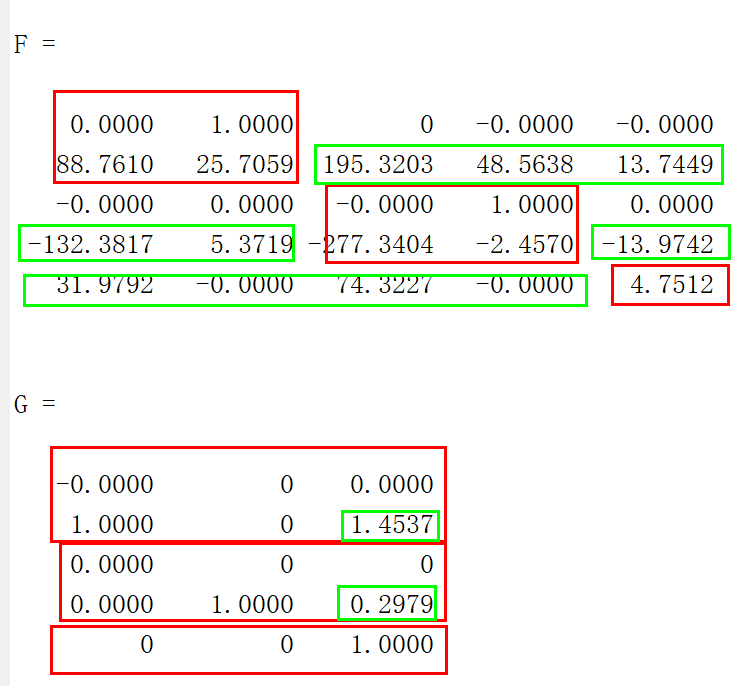
F=Tinv*A*inv(Tinv)
G=Tinv*B

这份程序给出了求标准型的办法。然而如果你增加维度，大概率会发生程序失败，那是因为求逆随着维度增加越来越困难了，所以这种标准型理论意义更大，算法的数值特性很差。

OK。我们来看上面两个图，5维系统F矩阵根据能控性指数2,2,1被分为了3个子系统，分别是2维，2维，1维，然后绿色的部分是相互耦合的系统状态。对于右上角的第一个系统，只有第一和第二个系统变量是属于这一个子系统的，剩下的第三到第五个状态不属于它，而是属于第二个子系统和第三个子系统的，所以如果这些状态变化了，就等效于第一个子系统的输入，也会令子系统的动态发生变化。反过来，第一个子系统的状态也是另外两个子系统的输入，各子系统之间相互影响。4维系统同理。  矩阵，也就是输入矩阵，5维系统由于有3个独立输入，所以被划分为了3个模块，也分别对应2,2,1。我们看到每个子系统都有一个独立的输入。绿色的部分是输入之间的耦合。输入之间的耦合是我们不想要的，现在我们设计一个方阵  ，使得输入矩阵  完全解耦，满足：

显然这样的  很容易找到：

我们得到：

然后我们给系统增加状态反馈，以抵消  中绿色框框里的状态，做到完全解耦。那么设计：

其中  是一个和  同尺寸的待设计矩阵。我们把(14)代入(13):

这就是MIMO系统的Brunovsky Canonical Form！我们发现最后能控的LTI系统变成了3个内部状态无耦合的子系统，我们分别写成：

所有的同维能控LTI系统都可以化成这个形式，因为等价是具有传递性的。我们这时候就可以自由单独设计  来实现各子系统的特征值分配了，也就是所谓的Pole Placement了。按照(14)我们可以反推出  ，得到实际控制律  。

看着美滋滋的，实际上MIMO系统的极点配置没有那么简单。以上只是根据Brunovsky Canonical Form进行计算增益矩阵  的特殊情况。一个MIMO系统  如果用  进行极点配置，实际上增益矩阵  的选择是不唯一的。就比如上面这个例子，我们可以配置子系统的特征值，按顺序[-1 -2 -3 -4 -5]和另一种[-2 -3 -4 -5 -1]配置，得到的最终系统的特征值是相同的，整体收敛速度是一样的。但是不同的顺序导致了两个闭环系统的系统矩阵  的特征向量不一样！特征向量的不同，这就导致了MIMO状态解的系数是不一样的（即振型不一样），最后状态变化的瞬态过程(transient)各不相同。所以增益的选择的多样性，造成了期望的选择最后要有一定的优越性。MATLAB中的place实际上已经是一种优化的算法了，感兴趣的可以去看看doc place。

讲到这里还要注意一点，这里我们没有讲输出方程  是怎么样的！实际上如果按照我们这样把系统进行transform，  矩阵是不会自动解耦的！也就是说我们虽然把系统分成了几个子系统，输入解耦了，但是输出还耦合在一起呢。一个子系统状态的变化，导致输出1发生变化，还有可能就会引发另一个输出2的变化。这离我们的终极目标-输入输出解耦其实还差一点。

MIMO的极点配置除了用静态反馈，还可以用动态反馈进行极点配置，这部分详见[7,p59]。

4.MIMO输入输出-状态反馈解耦 Decoupling via static state feedback

这篇文章其实本来是从刘豹《现代控制理论》第三版p204内容引申出来的，前前后后写了很多。书中写到两种解耦方式，一种是直接前馈串联补偿，使得整个系统拥有一个对角传递函数矩阵，只要待解耦系统的transfer function matrix是满秩的。当一个MIMO系统的传递函数阵不是对角矩阵的时候，输入可能是会同时影响多个输出的，这是显然的。我还没讲到传递函数矩阵，所以以后再说。第二种，就是我在上面介绍过的，求矩阵  ，用静态状态反馈来实现输入输出解耦。

定义：  是满足：  的最小整数  ，  ，  是  的每一行。
定义矩阵： 
定理：当独立输入输出数量相等时，LTI MIMO  能状态反馈解耦的充要条件是： 
定理：若LTI MIMO  能够状态反馈解耦的，则采用反馈律：  可以使得闭环系统  成为积分型解耦系统。其中  . 闭环系统的传递函数是一个对角传递函数矩阵。

我们现在用一个新的5维系统的例子来说明解耦的过程：

我们需要自己决定解耦后的  矩阵——也就是说我们需要自己手动写出解耦后的输出矩阵，比如我们让上面的5维系统的输出为一个  矩阵：

现在系统  有了，我们确定矩阵  :

对于这种随机的  矩阵，几乎所有的  都会等于0。这样我们很方便地就求出了  。然后我们求出：

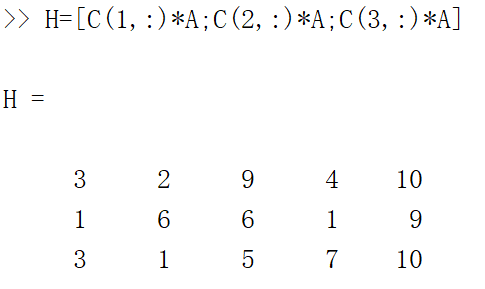
从而我们有增益矩阵  ：

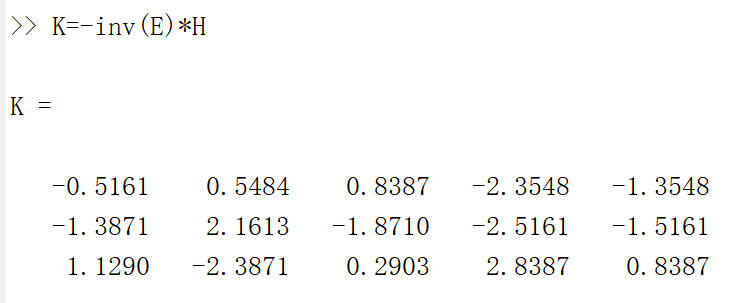
施加状态反馈后的闭环系统:

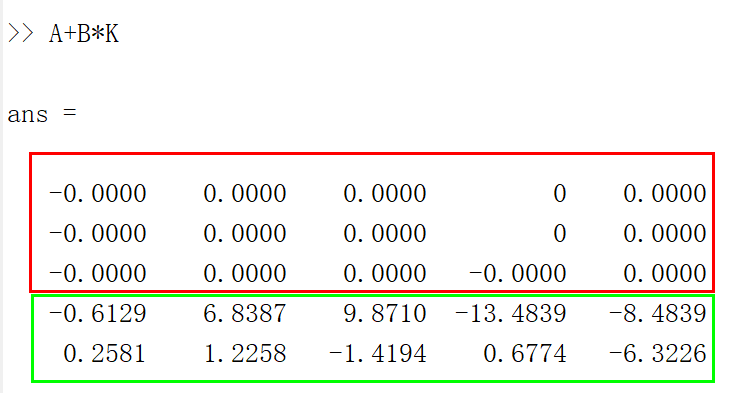
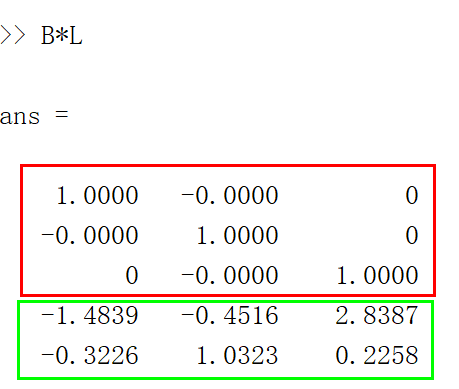
我们发现闭环系统的前三个状态构成了三个独立的子系统，实现了完全输入输出解耦！而最后两个状态却还是耦合着的，而且它们与输出之间已经脱钩了！解耦后的系统如果验证，依旧是可控的，并且我们现在可以单独控制前三个状态了，并且它们都唯一对应一个输出，完全解耦。但是最后剩下的两个状态其实已经不能从输出中得到了，这是什么现象？这不就是不能观嘛。你可以拿MATLAB小心验证一下能观性矩阵是不是不满秩，我给你答案：

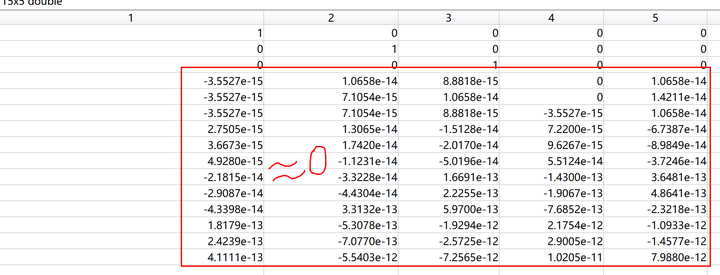
闭环系统的能观性矩阵秩实际上只有  （别看这么多数字，大部分接近0，就是不满秩）。这结果其实是显然的，你  矩阵里压根就没有最后两个状态（C中的绿色框），所以跟他们压根就没有关系。

但是注意啊，这些不能观的状态可是实实在在在闭环系统里的，而且你看A+BK中的绿框部分，它们还会受到3个子系统的控制的共同作用。这些状态虽然看不到，但是如果控制输入使得这些状态不是稳定的，那么就算前三个解耦的状态能够被很好地控制，整个系统也是不稳定的！

如果你学过非线性系统，或者将来我有机会还会写到，这就是所谓的内动态，是系统不能观的部分，但是又实实在在会影响到系统的稳定性。内动态的概念在线性系统中没有提及，而是在nonlinear system部分提出来了，可见确实nonlinear system对于学习者来说概念更加深刻和清晰。回到例子里，如果选择不同的输出矩阵，我们会得到不同维数和不同特性的内动态。所以在设计控制时，必须要保证内动态是稳定的，否则系统就会失稳最后Boom！

关于输入输出解耦在[7]中也进行了详细的讨论，是个不错的参考之处。而刘豹这本书在讲这块时个人感觉不是特别详尽，尤其是例子居然都是这么简单的，已经解耦了的系统，真的是很敷衍，指望学生看这例子学习？ 都没有告诉学生  矩阵是要自己选的用来解耦。

所以坑点都提示你了，自己用matlab试试去吧。

总结与Next

能控标准型的理论意义是非常大的，其实那么多标准型都是在做分析的时候用的到。因为能帮你搞清楚从理论上一个系统的结构，从而能够启发你去做研究，去解释一些实验里的现象。我的一些研究也曾经基于过线性系统理论和经典控制理论的一些结论，所以说脑子里没货，要用的时候就发愁。下一篇LQR控制吧。

觉得好的话点赞支持一下吧。其实更想看到你们积极的评论，至少让我知道你们有好好读，有问题一起交流吧。

Reference 参考文献

[1] Morgan, B. (1964). The synthesis of linear multivariable systems by state-variable feedback.IEEE Transactions on Automatic Control,9(4), 405-411.

[2] Falb, P., & Wolovich, W. (1967). Decoupling in the design and synthesis of multivariable control systems.IEEE transactions on automatic control,12(6), 651-659.

[3] Gilbert, E. G. (1969). The decoupling of multivariable systems by state feedback.SIAM Journal on Control,7(1), 50-63.

[4] Warren, M., & Mitter, S. (1975). Generic solvability of Morgan's problem.IEEE Transactions on Automatic Control,20(2), 268-269.

[5] 王东，周东华，金以慧(2001). 解耦问题的发展, 自动化博览, 04期.

[6] Levine, J. (2009).Analysis and control of nonlinear systems: A flatness-based approach. Springer Science & Business Media.

[7] 控制理论导论—从基本概念到研究前沿, 郭雷;程代展;冯德兴, 科学出版社 2005