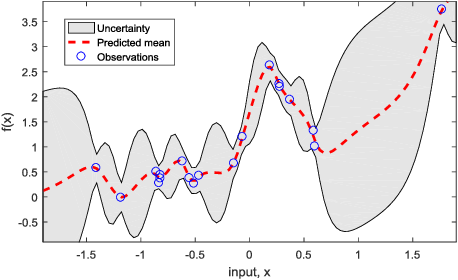
高斯过程将有限维高斯分布推广到了无限维，它是关于函数的分布。

Bayesian probabilistic approaches have many virtues, including their ability to incorporate prior knowledge and their ability to link related sources of information.

高斯过程由它的均值函数  和协方差函数

所决定，一个过程  是高斯过程可以记作  。

• marginalization property：新来的点不会影响到已有点的分布，这一性质可以让我们只关注观测点的分布，对于其他未观测点可以看作被边缘化(be marginalized out)了。

协方差函数（核函数）

在高斯过程中，协方差函数决定了采样的连续（光滑）性，协方差函数一般也被称为正（半）定核或者Mercel核。通常有两类核函数：平稳和非平稳。

平稳核函数具有平移不变性，两点之间的协方差只取决于它们之间的相对位置。比如Squared exponential (SE)，它对应无限个高斯型基函数的和

SE核函数的形式为

其中  是超参数分别代表信号的方差和length scale。

the longer the characteristic length scale, the more slowly varying the typical sample function is. The signal variance defines the vertical scale of variations of a sample function.

其他典型的核函数还有

高斯过程回归

在回归问题中，我们通常希望从  中学习潜在的映射关系  ，其中  是输入  对应的有噪观测。

在贝叶斯线性回归中，通常利用 个固定的基函数  来参数化潜在函数 

同时对于  我们可以赋予一定的先验，根据贝叶斯定理就可以得到参数的后验分布。

在高斯过程回归中（有时候也叫kriging），我们不需要参数化潜在的函数关系，而是直接将先验施加到函数空间上。

假设噪声项服从  ，则似然模型可以表示为

也就是说数据似然服从一个高斯分布，均值是训练输入对应的函数值，方差为噪声方差。

假设函数  的先验为一个零均值的高斯过程

我们可以得到高斯过程的后验为

其中  代表Gram矩阵  ，  为核函数，  代表一个输入固定为训练样本点的核函数。

回归的最终目标是要做预测，即给定  要预测 

接下来我们来看看预测分布。根据边缘化性质，我们知道训练输入的边缘分布为

输出关于输入的条件分布为

训练输出  和我们想要预测的  的联合分布为

其中

已知联合分布，我们可以求得条件分布，即预测分布为

其中

超参数优化

在实际使用中，通常核函数需要选择，同时和函数中涉及的超参数需要优化。

假设超参数  的先验为  ，它的后验分布为

第一项称为超参数的边际思染或者evidence，其对数形式为

其中  ，通过最大化边际似然函数即可得到超参数的估计值。如果采用梯度法进行优化，还需要求得对数边际似然函数的偏导数

剩下的事情就交给求解器吧

稀疏近似

高斯过程模型的一个缺陷在于求你Gram矩阵的计算量大，因此许多研究稀疏近似的办法来减小计算负担，大部分方法的思路都是仅使用  个潜在函数值，其他函数值用近似的方法替代。

通常引入一组潜在变量  ，它们对应输入  的潜在函数值，输入的选择不局限于训练或测试数据。潜在函数的联合分布可以进一步表示为

其中  。

为了近似引入假设：给定  ，  和  相互独立

因此可以得到近似表达式

其中  的形式和先前推导的预测分布一致（无噪声项）。

其他的近似算法不同在于假设不同，以及对条件分布的假设不同。

通过稀疏近似，计算复杂度从  降低至  。