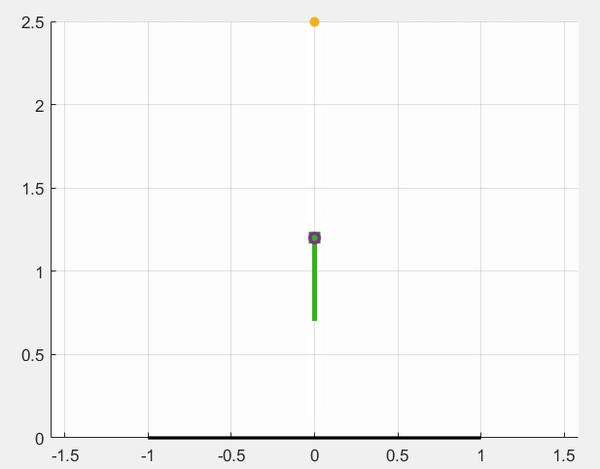
在之前的1D-SLIP模型中我们基于matlab的ODE45构建了其开环动力学的模型并进行了简单的跳跃仿真,在之前的模型中由于没有控制输入,弹簧在空中完全按牛顿定律进行自由落体运动,在支撑中则以弹簧的刚度阻尼模型改变自身的加速度,该模型即四足机器人或者足式机器人最简单的弹跳模型,基于虚拟模型理论将其产生的控制量输出即可以实现所谓的力伺服控制。
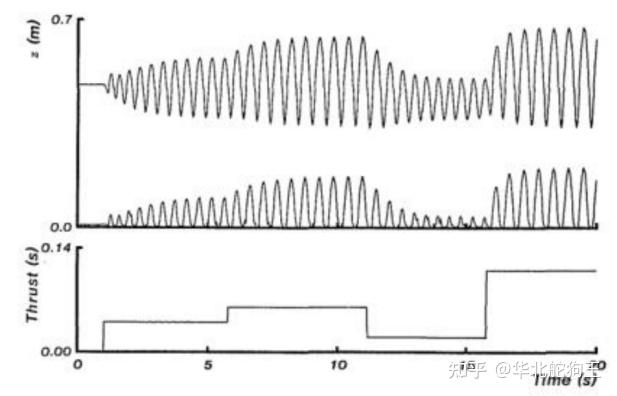
那我们现在设想一个最简单的规划控制问题,即弹簧从空中某个位置下落,我们希望规划支撑过程中的力来实现弹跳到固定的高度并且机体速度也是期望的结果,那传统的方法即基于能量准则来进行设计,假设期望的跳跃高度为H1,弹簧压缩到最短的高度为l_min,质量块质量为m,则所需要的弹性势能为mg(H1-l_min),一种最简单的方式是类似raibert早期单腿机器人采用的给定恒定力的方式,这个力可以在上述能量的基础上进行二次调节。
另外是可以采用MIT猎豹Bound论文中规划贝塞尔曲线的方式,其基于重力与阻力做功守恒的原理来确定所需要的平均力:
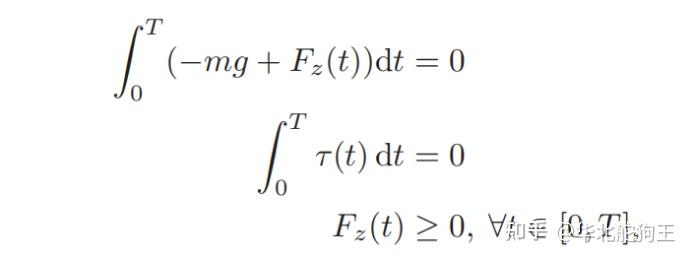
另外由于贝萨尔曲线的积分面积能很容易由其系数计算得到,这样就能由下式计算出贝塞尔曲线的幅值:
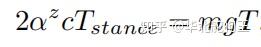
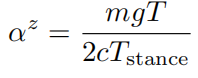
最终,得到在支撑中所需要产生的贝萨尔曲线:

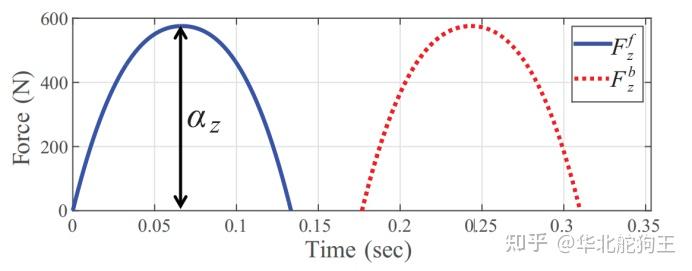
综上,上述两种方法都是基于能量来求取平均力幅值,最终规划相应支撑力实现的弹跳过程,其原理比较简单,但是对于更符合理解的形式是仅给定当前状态和期望状态就能规划出我们需要的力,当然里面需要系统的基本动力学模型,这样不但能将复杂的运动规划问题以模板的形式来实现,另外其通用和推广的可行性也更高。
这里我们就参考MatthewPeterKelly提供的matlab下的轨迹规划库来实现,对于上面的弹簧落体与弹跳规划问题,在一开始我采用的还是一个分段的动力学模型给定空中初始状态和弹跳后的期望状态来规划,仿真后发现这样是不行的,上面这样的规划问题由于存在两个不同的阶段和对应的动力学模型,因此需要独立进行处理,即首先在自由落体阶段仅基于ODE45来求解,当触地后以当前落地状态作为轨迹初始值,而轨迹末端则还是以弹跳的高度和速度为基础求解离地时的状态作为轨迹结束,这样我们仅采用优化库来规划支撑中的控制输出,当弹簧离地后又切换飞行模型进行求解,因此仿真的代码如下,首先构建两个独立的动力学模型,支撑阶段如下:
g=9.81;
num=length(z(1,:));
dx=zeros(1,num);
ddx=zeros(1,num);
if 1%仅考虑支撑
dx = z(2,:);%速度积分模型
ddx=-g-p.kp/p.m*(z(1,:)-p.l)-p.kd*z(2,:)/p.m+u/p.m;腾空飞行阶段模型如下:
g=9.81;
if z(1,:)>p.l%控制动力学
dx = z(2,:);%速度积分模型
ddx=-g; 则给定空中初始状态和弹跳末端状态:
%自由落体规划Phase
z0 = [
2.5, %Z位置
0 %dZ速度
];
%跳跃目标
z_tar = [
1.2, %Z位置
0.0 %dZ速度
];
首先,用动力学求解落地瞬间的系统状态:
if z0(1)>param.l
t_touch=(2*(z0(1)-param.l )/param.g)^0.5;
tSpan = [0,t_touch];
ctrlFun = @(z)( zeros(size(z(1,:))) );
dynFun = @(t,z)( cartPoleDynamics(z, ctrlFun(z), param) );
%%%% Simulate the system!
options = odeset(...
'RelTol',1e-8, ...
'AbsTol',1e-8);
sol = ode45(dynFun, tSpan, z0, options);
%%%% Unpack the simulation
T_sample=int16(tSpan(2)*T_sample_r);
t_p1 = linspace(tSpan(1), tSpan(2), T_sample);
z_p1 = deval(sol,t_p1);%模拟系统状态
u_p1 = ctrlFun(z_p1);
ztd = [
z_p1(1,T_sample), %Z位置
z_p1(2,T_sample) %dZ速度
];
else%非自由落体
ztd = z0;
z_p1=ztd;
end
在支撑中,首先基于跳跃期望状态计算离地速度,离地高度即为弹簧原长:
%--------------------------支撑规划Phase--------------------------
%计算离地状态
v_lf=((param.m *param.g*(z_tar(1)-param.l)+0.5*param.m *z_tar(1)^2)/(0.5*param.m ))^0.5;
ze = [
param.l, %pos
v_lf %spd
];
之后构建轨迹规划问题,带入对应的支撑动力学模型:
duration = 0.35; %时间限制
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~%
% Set up function handles %
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~%
problem.func.dynamics = @(t,x,u)( cartPoleDynamics_OPT(x,u,param) );%定义系统动力学
problem.func.pathObj = @(t,x,u)( u.^2 ); %Force-squared cost function
%problem.func.pathObj = @(t,x,u)( ones(size(t)) );
设定对状态、时间和控制输入的约束:
%始末条件
problem.bounds.initialState.low = ztd;
problem.bounds.initialState.upp = ztd;
problem.bounds.finalState.low = ze;%末端竖直状态
problem.bounds.finalState.upp = ze;
problem.bounds.state.low = [param.l_min;-inf];%系统状态位置状态限制
problem.bounds.state.upp = [param.l; inf];
problem.bounds.control.low = -maxForce;%控制输入状态约束
problem.bounds.control.upp = maxForce;确定轨迹优化的方法:
method = 'chebyshev';
switch method
case 'chebyshev'
problem.options.method = method;
problem.options.chebyshev.nColPts = 5;
case 'trapezoid'
problem.options.method = method;
case 'hermiteSimpson'
problem.options.method = method;
problem.options.hermiteSimpson.nSegment = 15;
problem.options.nlpOpt.MaxFunEvals = 5e4;
case 'gpops'
problem.options.method = 'gpops';
otherwise
error('invalid method')
end
之后求解轨迹:
%problem.options.rungeKutta.nSubStep
soln = optimTraj(problem);
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~%
% Display Solution %
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~%
%%%% Unpack the simulation
T_sample=int16((soln.grid.time(end)-soln.grid.time(1))*T_sample_r);
t_p2 = linspace(soln.grid.time(1), soln.grid.time(end), T_sample);
z_p2 = soln.interp.state(t_p2);%系统状态
u_p2 = soln.interp.control(t_p2);%控制输入则最后将轨迹末端的状态作为离地的初始值,以ODE45采用飞行动力学进行求解:
%离地飞行Phase
zlf = [
z_p2(1,T_sample), %Z位置
z_p2(2,T_sample) %dZ速度
];
t_hmax=2*zlf(2)/param.g/2 ;
tSpan = [0,t_hmax];
ctrlFun = @(z)( zeros(size(z(1,:))) );
dynFun = @(t,z)( cartPoleDynamics(z, ctrlFun(z), param) );
%%%% Simulate the system!
options = odeset(...
'RelTol',1e-8, ...
'AbsTol',1e-8);
sol = ode45(dynFun, tSpan, zlf, options);
%%%% Unpack the simulation
T_sample=int16(tSpan(2)*T_sample_r);
t_p3 = linspace(tSpan(1), tSpan(2), T_sample);
z_p3 = deval(sol,t_p3);%模拟系统状态
u_p3 = ctrlFun(z_p1);
%全流程绘制
z_p33=z_p3(:,1:length(z_p3(1,:)));
z_draw = cat(2,z_p1(:,1:length(z_p1(1,:))-1),z_p2(:,1:length(z_p2(1,:))-1),z_p33);
[p_com,p_leg] = cartPoleKinematics(z_draw,param);%计算每个时刻各部分的运动学
xLow = -1;
xUpp = 1;
yLow = min(p_leg);
yUpp = max(p_com);
Limits = [xLow,xUpp,yLow,yUpp];
drawAnim_OPT(z_draw,param,Limits,duration/1000)最终的仿真结果如下,可以看到机器人从2.5m下落,最终弹跳到了期望高度1.2m左右,当然速度也是期望的0,最终的控制输出可以看到其按着执行器实际的最大能力进行了饱和,因此轨迹规划相比之前的方法还是高级很多。
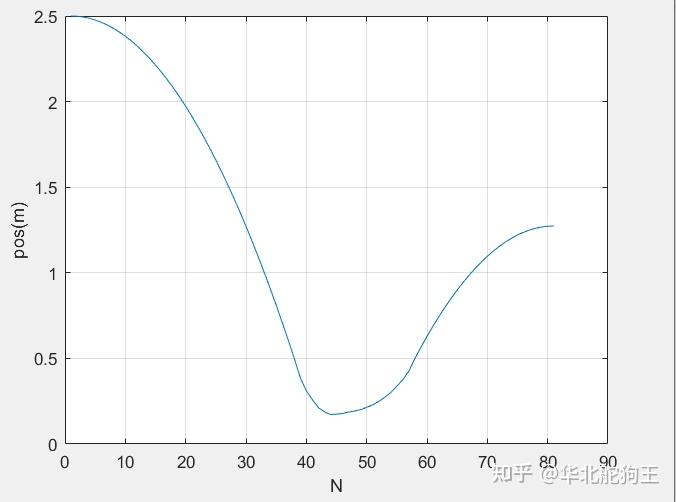
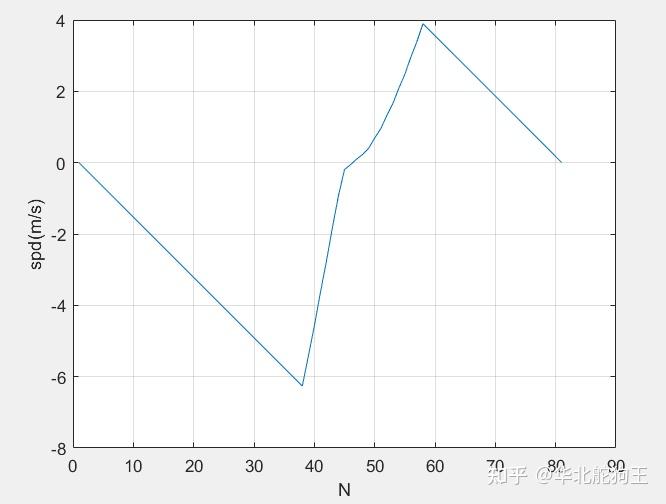
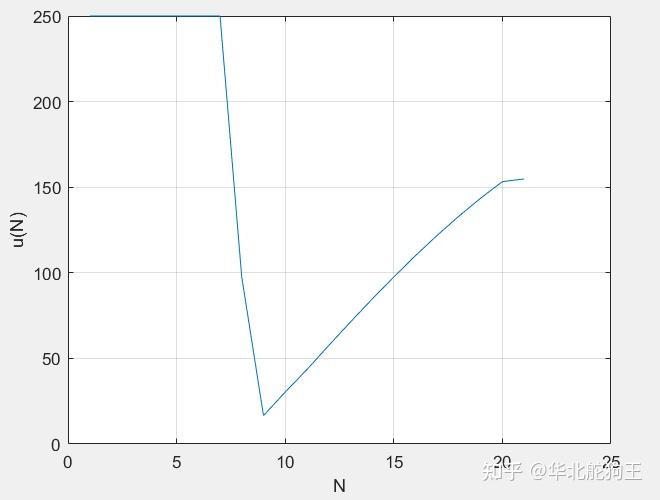
以上就是一个最简单的1D-SLIP模型弹跳规划的例子,当然其存在很多问题,第一是代码结构比较复杂,而是当系统状态增加时上述方法无法在适用,特别是支撑和腾空是通过串行书写的方式来实现,要实现多个周期的弹跳那代码将会很长,因此在下一个文章中我会采用ODE45自带的事件触发机制来自动实现状态的切换,同时构建2D-SLIP模型并在其上验证raibert早期提出的落足点选择算法。
仿真代码在demo中SLIP-1D的MAIN_minForce.m:
链接:https://pan.baidu.com/s/17fiJOBt7gKlfH87ozqQxXQ
提取码:qy65
--来自百度网盘超级会员V1的分享






评论(0)
您还未登录,请登录后发表或查看评论