机器视觉与控制——轨迹(下)

 前言

       轨迹是具有特定时间属性的一条路劲，其中一个重要特征是要平滑（位置和姿态随时间流畅地变化），文章分俩篇将从一维扩展到多维，最后讨论如何生成分段性轨迹，使得机器人不间断地经过一系列中间点。

多段轨迹

       对于多轴的情况,很可能在某个特定运动段其中一些轴要比其他轴需要移动更多距离,这时如果各个关节有不同的速度限制时,将会使轨迹生成变得复杂.为解决上述问题,第一步需要确定哪个轴将是完成最慢的,依据是每个轴对应这个运动段的运动距离以及该轴最大可达速度.算出该段的运动持续时间和各轴实际所需的速度,确保所有轴在同一时间达到下一个目标Xk.

       工具箱函数mstraj可以基于中间点矩阵生成一个多段多轴轨。Eg:有四个中间点的两轴运动可以用以下方法生成：

函数mstraj的第一个参数是中间点矩阵，每点对应矩阵的一行。剩余的参数分别是：每轴的最大速度向量，每段的运动时间向量，起点各轴坐标，采用时间间隔，以及加速时间。函数mstraj返回一个矩阵，行对应的是时间每步，列对应的是各个轴。没用提供输出参数时mstraj会默认绘制出轨迹曲线，如图3.5（a）所示。从例子不难发现第一个轴的最大速度比第二个轴更大。而在最后一个运动段，两轴是以相同的速度运动的，因为这段的运动时间是由最慢的轴决定的。

  如果增加加速时间：

轨迹会变得更圆滑，如图3.5（b）。因为轨迹上有更多的时间来完成多项式曲线段的混合。

这个函数只是简单地对向量代表的位姿进行插值。单这个函数不是对坐标系旋转进行插值的理想方式。

三维空间姿态插值

       在机器人学中，经常需要对姿态进行插值。Eg：我们需要机器人的末端执行器平滑地从姿态ξ0到ξ1.需要找到某个函数ξ（s）=σ（ξ0，ξ1，s），s属于【0，1】.其中ξ地具体表示法很大程度上决定能否使函数平滑地经过s内定义的一系列中间位姿。

一个可行且常见的选择是尝试三角度表示法，如欧拉角或横滚-俯仰-偏航角，，线性插值法：

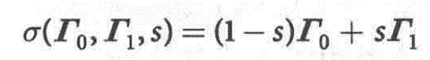
Eg：定义两个姿态：

得到等价横滚-俯仰-偏航角：

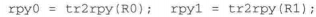
分50个时间步在它们之间生成一条轨迹：

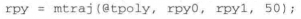
通过动画演示，很容易观察轨迹变化过程：

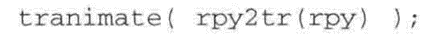
从坐标系的旋转轴线沿轨迹的变化可以看出，因为姿态变化较大，动作虽然平滑但是不太协调。如果用三角度系统中有ξ0或ξ1之一接近奇异点，也会出问题。

笛卡儿运动

       一个常见的需求是在SE（3）中生成俩位姿之间的光滑路径，同时涉及位置及姿态的变化。在机器人学中这通常被称为笛卡儿运动。

       将初始和最终姿态都表示齐次变换矩阵：

工具箱函数trinterp提供了沿路径单位化距离s属于【0，1】中的位姿插值。Eg：其中间的位姿是

其中平移部分是用线性插值，旋转部分是用四元数插值法interp进行球形插值。

两个位姿之间50个分步的轨迹可用以下方法生成：

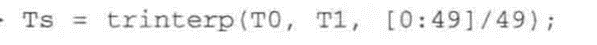
参数分别对应的是起点和终点的位姿，以及从0到1线性变化的路径长度。由此产生的轨迹Ts是一个三维矩阵：

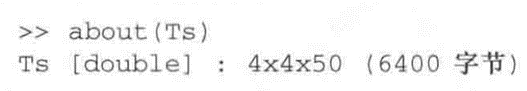
代表的是每个时间分步对应的齐次变换矩阵（前两个指数4×4）.路径上第一点的齐次变换是：

简单直观的表现方法是通过动画：

它将展现出坐标系从位姿T1平移、旋转到位姿T2的变化过程。

       轨迹的平移部分由以下方式获得：

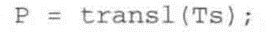
       以矩阵形式返回轨迹的笛卡儿位置坐标：

位置向量的变化可以用plot函数画出：

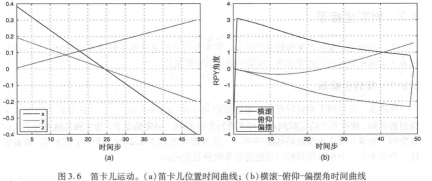
如图3.6（a）所示。图3.6（b）还展示了以横滚-俯仰-偏摆角格式画的姿态变化曲线：

从图中看到，位置坐标随时间的变化既平滑又呈线性，而姿态随时间的变化也平滑，但不是线性的。

虽然轨迹在空间中是平滑的，但沿轨迹的步距s在时间上并不平滑。路径起点上的速度值从零跳跃到有限值，然后在终点又突降至零—没有相应的起始加速和结束减速。用标量函数tpoly和lspb来创建一个时间上平滑的s，这样路径的运动也平滑了。只需将传递给trinterp的第三个参数更改为一个沿路径的单位化距离向量即可：

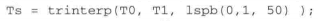
轨迹是不会变的，但这时坐标系会沿路径逐渐加速到一个恒定速度，然后结束时再减速，从3.7（b）中轨迹姿态部分较光滑的曲线反映出来。工具箱中提供了一个方便的速记函数ctraj来进行轨迹插值：

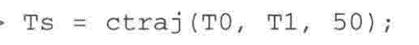
参数时初始，最终位姿，分步数量。