3.1 轨迹

轨迹是具有特定时间属性的一条路径。

3.1.1 平滑一维轨迹

一个真正的机器人关节都有一个额定的最大速度，而且为了使关节运动时间最短，应使其运行在最大速度上的时间尽可能长。因此我们希望速度曲线的顶部是一条直线。

混合曲线轨迹：延长最大速度运行时间，使得速度曲线顶部为一平直线，两侧为加减速段。

3.1.2 多维的情况

大多数实用的机器人都有一个以上的运动轴或自由度。我们将其用向量形式表示为X∈ RM,M代表自由度的数目。轮式移动机器人由它的位置(x, y)或位姿(x,y,θ)来描述，而关节臂式机器人的末端工具则有位置(x,y,z)，姿态(θr,θp ,θy)，或位姿(x, y, z, θr,θp ,θy)。因此我们需要从初始位姿向量到最终位姿向量的多维平滑运动。

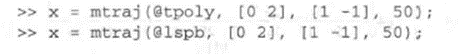
3.1.3 多段轨迹

机器人应用中经常需要机器人平滑地沿一条路径运动，并不停顿地经过一个或多个中间节点。为了实现速度连续，舍弃中间点位置，采用直线和曲线拟合：

3.1.4 三维空间姿态插值

采用线性插值法

3.2 时变坐标系

3.2.1 旋转坐标系

物体在三维空间中旋转时有一个角速度向量ω=(ωx,ωy,ωz)\omega=(\omega_x, \omega_y, \omega_z)ω=(ωx,ωy,ωz)。这个向量的方向定义了瞬时转动轴，即在某个特定时间点坐标系旋转所绕的轴。通常情况下，这个轴是随时间变化而改变的。向量长度代表绕该轴的转速，这有点类似于旋转的角轴表示法。力学中有一个众所周知的时变旋转矩阵微分表达式(理论力学)：

 R˙(t)=S(ω)R(t)\dot{R}(t)=S(\omega)R(t)R˙(t)=S(ω)R(t)式中：R(t)R(t)R(t) 为空间旋转矩阵；S(w)S(w)S(w) 为角速度矩阵，其具体形式如下：

 R(t)=(nxoxaxnyoyaynzozaz)S(ω)=(0−ωzωyωz0−ωx−ωyωx0)\begin{matrix}

 R\text{(}t\text{)}=\left( \begin{matrix}

 n_x&o_x&a_x\\

 n_y&o_y&a_y\\

 n_z&o_z&a_z\\

 \end{matrix} \right)&S\left( \omega \right) =\left( \begin{matrix}

 0&-\omega _z&\omega _y\\

 \omega _z&0&-\omega _x\\

 -\omega _y&\omega _x&0\\

 \end{matrix} \right)\\

 \end{matrix}R(t)=⎝⎛nxnynzoxoyozaxayaz⎠⎞S(ω)=⎝⎛0ωz−ωy−ωz0ωxωy−ωx0⎠⎞利用机器人工具箱，可以得到

 >> S = skew([1 2 3])

 S =

 0 -3 2

 3 0 -1

 -2 1 0

 工具箱函数vex具有逆解的功能：将斜对称矩阵转换成一个向量：

 >> vex(S)

 ans =

 1

 2

 3

那么方程中的 R˙\dot RR˙ 是什么意思呢？我们用微分近似法可得

 R˙≈R(t+δt)−R(t)δt\dot{R}\approx\dfrac{R(t+\delta_t)-R(t)}{\delta_t}R˙≈δtR(t+δt)−R(t)即

 R(t+δt)≈δtR˙+R(t)R(t+\delta_t)\approx\delta_t\dot{R}+R(t)R(t+δt)≈δtR˙+R(t)将其代入方程中，得到

 R(t+δt)≈δtS(ω)R(t)+R(t)=(δtS(ω)+I3×3)R(t)R(t+\delta_t)\approx\delta_tS(\omega)R(t)+R(t)=(\delta_tS(\omega)+I_{3\times 3})R(t)R(t+δt)≈δtS(ω)R(t)+R(t)=(δtS(ω)+I3×3)R(t)它描述了标准正交旋转矩阵是如何作为一个角速度的函数变化的。

3.2.2 增量运动

现在考虑一个坐标系经微小旋转从 R0R_0R0 变到 R1R_1R1。这时可以将上个方程写为

 R1=(δtS(ω)+I3×3)R0R_1=(\delta_tS(\omega)+I_{3\times3})R_0R1=(δtS(ω)+I3×3)R0将上式重新整理后，得

 δtS(ω)=R1R0T−I3×3\delta_tS(\omega)=R_1R_0^T-I_{3\times3}δtS(ω)=R1R0T−I3×3再对其两侧均使用运算符vex，即求 S(ω)S(\omega)S(ω)的逆，得到

 δθ=vex(R1R0T−I3×3)\delta_\theta=\text{vex}(R_1R_0^T-I_{3\times3})δθ=vex(R1R0T−I3×3)其中，δθ=δtω\delta_\theta = \delta_t\omegaδθ=δtω 是一个三维向量，单位是角度，它表示一个绕世界坐标系的 xxx、yyy 和 zzz 三轴的无穷小转动。

 我们之前强调过旋转变换的不可交换性，但对于无穷小角度变化的乘法来说却是可交换的。可以用具体数字的例子说明如下：

 >> Rdelta = rotx(0.001) * roty(0.002) * rotz(0.003)

 Rdelta =

 1.0000 -0.0030 0.0020

 0.0030 1.0000 -0.0010

 -0.0020 0.0010 1.0000

 以上结果是与下面的计算相同的(取4位有效数字)：

 >> Rdelta = roty(0.002) * rotx(0.001) *rotz(0.003)

 Rdelta =

 1.0000 -0.0030 0.0020

 0.0030 1.0000 -0.0010

 -0.0020 0.0010 1.0000

 使用前面推导的方程，可以重新获得上面矩阵对应的微小旋转角 δθ\delta_\thetaδθ：

 >> vex(Rdelta - eye(3, 3))

 ans =

 0.0010

 0.0020

 0.0030

 现在给出两个差异极小的位姿 ξ0\xi_0ξ0 和 ξ1\xi_1ξ1，可以用一个六维向量来表示它们间的差异：

 δ=Δ(ξ0,ξ1)=(δd,δθ)\delta=\Delta(\xi_0, \xi_1)=(\delta_d, \delta_\theta)δ=Δ(ξ0,ξ1)=(δd,δθ)它由位移增量和旋转增量两部分组成。δ∈R6\delta\in\mathbb{R}^6δ∈R6 的值实际上是用空间速度乘以 δt\delta_tδt 得到的。如果位姿都用齐次变换矩阵的形式表示，那么位姿差异是

 δ=Δ(T0,T1)=(t1−t0vex(R1R0T−I3×3))\delta=\Delta(T_0, T_1)=\left( \begin{array}{c}

 t_1-t_0\\[1em]

 \text{vex}\left( R_1R_0^T-I_{3\times 3} \right)\\

 \end{array} \right)δ=Δ(T0,T1)=⎝⎛t1−t0vex(R1R0T−I3×3)⎠⎞其中，T0=(R0,t0)T_0=(R_0, t_0)T0=(R0,t0)，T1=(R1,t1)T_1=(R_1, t_1)T1=(R1,t1)。在工具箱中它可以用函数tr2delta求得。

 方程的逆运算为

 ξ=Δ−1(δ)\xi=\Delta^{-1}(\delta)ξ=Δ−1(δ)而齐次变换表示法的逆运算是

 T=(Sδθδd03×10)+I4×4T=\left( \begin{matrix}

 S\delta _{\theta}&\delta _d\\

 0_{3\times 1}&0\\

 \end{matrix} \right) +I_{4\times4}T=(Sδθ03×1δd0)+I4×4在工具箱里它用函数delta2tr求解。

 >> T0 = transl(1,2,3)*trotx(1)*troty(1)*trotz(1);

 >> T1 = T0*transl(0.01,0.02,0.03)*trotx(0.001)*troty(0.002)*trotz(0.003)

 T1 =

 0.2889 -0.4547 0.8425 1.0191

 0.8372 -0.3069 -0.4527 1.9887

 0.4644 0.8361 0.2920 3.0301

 0 0 0 1.0000

 函数 Δ(⋅)\Delta(\cdot)Δ(⋅) 的计算是由工具箱函数tr2delta完成的：

 >> d = tr2delta(T0, T1);

 >> d'

 ans =

 0.0191 -0.0113 0.0301 0.0019 -0.0011 0.0030

 该位姿变化(位移)由相对于世界坐标系的平移增量和旋转增量组成。给定这个位移量以及初始位姿，可求得最终位姿为

 >> delta2tr(d) * T0

 ans =

 0.2889 -0.4547 0.8425 1.0096

 0.8372 -0.3069 -0.4527 1.9859

 0.4644 0.8361 0.2920 3.0351

 0 0 0 1.0000

 它非常接近于上面T1给出的真实值，误差是由于位移量不是无穷小这一事实所致。