多传感器融合定位理论基础（十一）：IMU预积分模型及应用

一、概述

在上一篇文章中，我们给出了下面的框图中实现框图对应的理论部分，但是也提到，虚线对应的部分太过复杂，当时没有介绍。

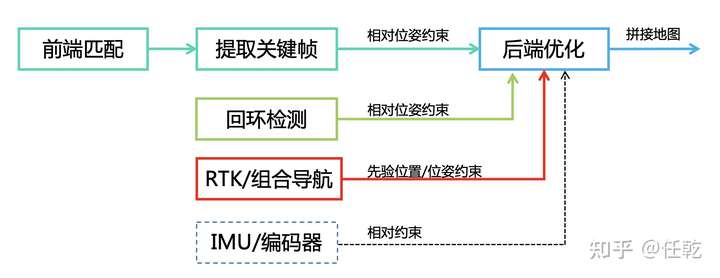
下面来分析一下具体的原因。带IMU的融合模型中的优化问题可以表示为

三种约束分别通过以下方式获得：

1) 激光里程计约束：使用激光里程计，计算每个关键帧位姿，进而得到相对位姿；

2) IMU约束：在上一个关键帧位姿基础上，进行惯性积分，从而得到两关键帧相对位姿；

3) RTK约束：直接测量得到。

此时融合流程可以用下面的流程图表示

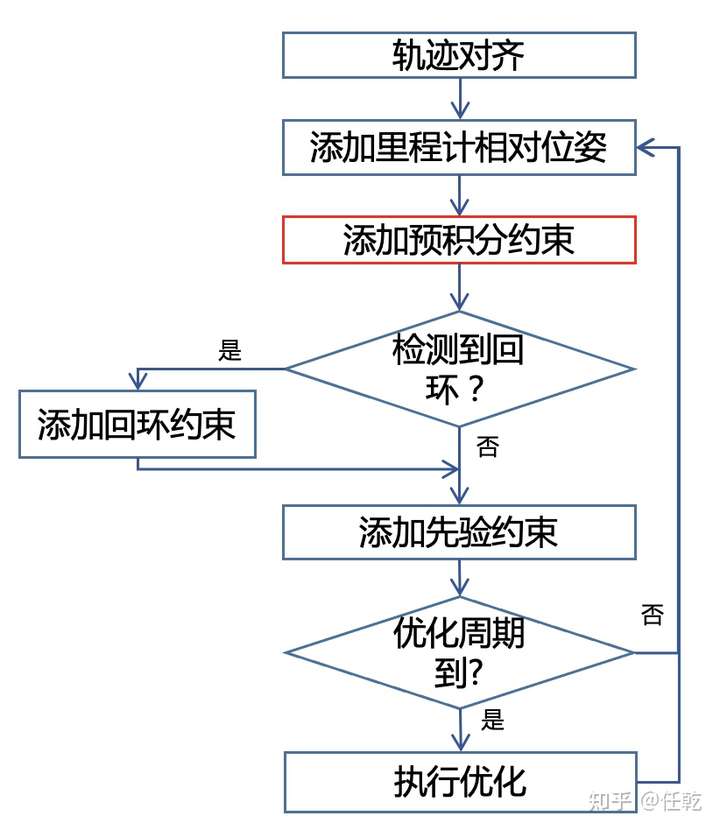
这个流程图中，红色部分是本篇文章新增的IMU约束对应的环节，剩下的部分就是上一篇文章对应的流程了。所以从这个框图中也可以看出这两篇文章在内容上的分工了。

二、预积分问题引入

这种融合模型的核心问题在于，IMU的约束是通过惯性积分得到的，而惯性积分是以它前一时刻的位姿为初始值得到的，但是位姿每次优化后会发生变化，这导致其后的IMU惯性积分就要重新进行，显然运算量过大。

这个问题的解决思路就是直接计算两帧之间的相对位姿，而不依赖初始值影响，即所谓的预积分。本篇文章剩余的篇幅就几乎全在讨论预积分的问题。

三、预积分模型介绍

在前面的惯性导航文章中，已知导航的微分方程如下

$\begin{equation} \dot{\mathbf{p}}_{w b_{t}}=\mathbf{v}_{t}^{w} \end{equation}(1)\\$

$\begin{equation} \dot{\mathbf{v}}_{t}^{w}=\mathbf{a}_{t}^{w} \end{equation}(2)\\$

$\begin{equation} \dot{\mathbf{q}}_{w b_{t}}=\mathbf{q}_{w b_{t}} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array}\right] \end{equation}(3)\\$

根据该微分方程，可知从 i 时刻到 j 时刻 IMU的积分结果为

$\begin{equation} \mathbf{p}_{w b_{j}}=\mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t+\iint_{t \in[i, j]}\left(\mathbf{q}_{w b_{t}} \mathbf{a}^{b_{t}}-\mathbf{g}^{w}\right) \delta t^{2} \end{equation}(4)\\$

$\begin{equation} \mathbf{v}_{j}^{w}=\mathbf{v}_{i}^{w}+\int_{t \in[i, j]}\left(\mathbf{q}_{w b_{t}} \mathbf{a}^{b_{t}}-\mathbf{g}^{w}\right) \delta t \end{equation}(5)\\$

$\begin{equation} \mathbf{q}_{w b_{j}}=\int_{t \in[i, j]} \mathbf{q}_{w b_{t}} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array}\right] \delta t \end{equation}(6)\\$

根据预积分的要求，需要求相对结果，而且不依赖于上一时刻位姿，因此需要对上式做转换。

由于

$\begin{equation} \mathbf{q}_{w b_{t}}=\mathbf{q}_{w b_{i}} \otimes \mathbf{q}_{b_{i} b_{t}} \end{equation}$ ，把它带入(4)-(6)式可得

$\begin{equation} \mathbf{p}_{w b_{j}}=\mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \iint_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t^{2} \end{equation}(7)\\$

$\begin{equation} \mathbf{v}_{j}^{w}=\mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \int_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t \end{equation}(8)\\$

$\begin{equation} \mathbf{q}_{w b_{j}}=\mathbf{q}_{w b_{i}} \int_{t \in[i, j]} \mathbf{q}_{b_{i} b_{t}} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array}\right] \delta t \end{equation}(9)\\$

以上三个式子中，积分符号里面的项，就是需要预积分的项，可见，他们已经完全和i时刻的状态无关了。

为了整理公式，把积分相关的项用下面的式子代替

$\begin{equation} \boldsymbol{\alpha}_{b_{i} b_{j}}=\iint_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t^{2} \end{equation}(10)\\$

$\begin{equation} \boldsymbol{\beta}_{b_{i} b_{j}}=\int_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t \end{equation}(11)\\$

$\mathbf{q}_{b_{i} b_{j}}=\int_{t \in[i, j]} \mathbf{q}_{b_{i} b_{t}} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array}\right] \delta t(12)\\$

实际使用中使用离散形式，而非连续形式，由于在解算中，一般采用中值积分方法，即

$\boldsymbol{\omega}=\frac{1}{2}\left[\left(\boldsymbol{\omega}^{b_{k}}-\mathbf{b}_{k}^{g}\right)+\left(\boldsymbol{\omega}^{b_{k+1}}-\mathbf{b}_{k}^{g}\right)\right](13)\\$

$\mathbf{a}=\frac{1}{2}\left[\mathbf{q}_{b_{i} b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)+\mathbf{q}_{b_{i} b_{k+1}}\left(\mathbf{a}^{b_{k+1}}-\mathbf{b}_{k}^{a}\right)\right](14)\\$

那么预积分的离散形式可以表示为

$\boldsymbol{\alpha}_{b_{i} b_{k+1}}=\boldsymbol{\alpha}_{b_{i} b_{k}}+\boldsymbol{\beta}_{b_{i} b_{k}} \delta t+\frac{1}{2} \mathbf{a} \delta t^{2}(15)\\$

$\boldsymbol{\beta}_{b_{b} b_{k+1}}=\boldsymbol{\beta}_{b_{i} b_{k}}+\mathbf{a} \delta t(16)\\$

$\mathbf{q}_{b_{i} b_{k+1}}=\mathbf{q}_{b_{i} b_{k}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \boldsymbol{\omega} \delta t \end{array}\right](17)\\$

经过以上的推导，此时状态更新的公式可以整理为

$\left[\begin{array}{c} \mathbf{p}_{w b_{j}} \\ \mathbf{v}_{j}^{w} \\ \mathbf{q}_{w b_{j}} \\ \mathbf{b}_{j}^{a} \\ \mathbf{b}_{j}^{g} \end{array}\right]=\left[\begin{array}{c} \mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ \mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{q}_{w b_{i}} \mathbf{q}_{b_{i} b_{j}} \\ \mathbf{b}_{i}^{a} \\ \mathbf{b}_{i}^{g} \end{array}\right]\\$

需要注意的是，陀螺仪和加速度计的模型为

$\mathbf{b}_{k+1}^{a}=\mathbf{b}_{k}^{a}+\mathbf{n}_{\mathbf{b}_{k}^{a}} \delta t\\$

$\mathbf{b}_{k+1}^{g}=\mathbf{b}_{k}^{g}+\mathbf{n}_{\mathbf{b}_{k}^{g}} \delta t\\$

即认为bias是在变化的，这样便于估计不同时刻的bias值，而不是整个系统运行时间内都当做常值对待。这更符合低精度mems的实际情况。但在预积分时，由于两个关键帧之间的时间较短，因此认为i和j时刻的bias相等。

需要注意的一点是，预积分的结果中包含了bias，在优化过程中，bias作为状态量也会发生变化，从而引起预积分结果变化。为了避免bias变化后，重新做预积分，可以把预积分结果在bias处泰勒展开，表达成下面的形式，这样就可以根据bias的变化量直接算出新的预积分结果。

$\boldsymbol{\alpha}_{b_{i} b_{j}}=\overline{\boldsymbol{\alpha}}_{b_{i} b_{j}}+\mathbf{J}_{b_{i}^{\alpha}}^{\alpha} \delta \mathbf{b}_{i}^{a}+\mathbf{J}_{b_{i}^{g}}^{\alpha} \delta \mathbf{b}_{i}^{g}\\$

$\boldsymbol{\beta}_{b_{i} b_{j}}=\overline{\boldsymbol{\beta}}_{b_{i} b_{j}}+\mathbf{J}_{b_{i}^{\alpha}}^{\beta} \delta \mathbf{b}_{i}^{a}+\mathbf{J}_{b_{i}^{g}}^{\beta} \delta \mathbf{b}_{i}^{g}\\$

$\mathbf{q}_{b_{i} b_{j}}=\overline{\mathbf{q}}_{b_{i} b_{j}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_{i}^{g}}^{q} \delta \mathbf{b}_{i}^{g} \end{array}\right]\\$

其中

$\mathbf{J}_{b_{i}^{a}}^{\alpha}=\frac{\partial \boldsymbol{\alpha}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{a}}\\$

$\mathbf{J}_{b_{i}^{g}}^{\alpha}=\frac{\partial \boldsymbol{\alpha}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{g}}\\$

$\mathbf{J}_{b_{i}^{a}}^{\beta}=\frac{\partial \boldsymbol{\beta}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{a}}\\$

$\mathbf{J}_{b_{i}^{g}}^{\beta}=\frac{\partial \beta_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{g}}\\$

$\mathbf{J}_{b_{i}^{g}}^{q}=\frac{\mathbf{q}_{b_{i} b_{j}}}{\partial \mathbf{b}_{i}^{g}}\\$

此处暂时只直接给出以上各雅可比的结果，它的推导放在后面进行。

四、预积分在优化中的使用

1.使用思路

1）凸优化回顾

损失函数由残差函数组成

$\min _{x} F(x)=\frac{1}{2}\|f(x)\|_{2}^{2}\\$

当考虑方差时，可以写为

$\min _{x} F(x)=f(x)^{T} \Omega f(x)\\$

利用高斯牛顿方法，求解该优化问题，需要解下面的方程

$\underbrace{J^{T} \Omega J}_{H} \Delta x=\underbrace{-J^{T} \Omega f(x)}_{g}\\$

即，在优化中使用一项信息，需要设计残差，并推导它的雅可比和方差

2）预积分的使用

按照优化的套路，在优化中使用预积分，需要：

a.设计残差

b.推导残差关于待优化变量的雅可比

c.计算残差的方差

除此以外，预积分中还多一项计算，即推导bias变化时，预积分量重新计算的方法(上面提到过的)。

2. 残差设计

在优化时，需要知道残差关于状态量的雅可比。由于已知姿态位姿更新的方法如下

$\left[\begin{array}{c} \mathbf{p}_{w b_{j}} \\ \mathbf{q}_{w b_{j}} \\ \mathbf{v}_{j}^{w} \\ \mathbf{b}_{j}^{a} \\ \mathbf{b}_{j}^{g} \end{array}\right]=\left[\begin{array}{c} \mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ \mathbf{q}_{w b_{i}} \mathbf{q}_{b_{i} b_{j}} \\ \mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{b}_{i}^{a} \\ \mathbf{b}_{i}^{g} \end{array}\right]\\$

因此，可以很容易写出一种残差形式如下：

$\left[\begin{array}{c} \mathbf{r}_{p} \\ \mathbf{r}_{q} \\ \mathbf{r}_{v} \\ \mathbf{r}_{b a} \\ \mathbf{r}_{b g} \end{array}\right]=\left[\begin{array}{c} \mathbf{p}_{w b_{j}}-\mathbf{p}_{w b_{i}}-\mathbf{v}_{i}^{w} \Delta t+\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}-\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \\ \mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t-\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{b}_{j}^{a}-\mathbf{b}_{i}^{a} \\ \mathbf{b}_{j}^{g}-\mathbf{b}_{i}^{g} \end{array}\right]\\$

但是和预积分相关的量，仍然与上一时刻的姿态有关，无法直接加减，因此，把残差修正为以下形式

$\begin{equation} \left[\begin{array}{c} \mathbf{r}_{p} \\ \mathbf{r}_{q} \\ \mathbf{r}_{v} \\ \mathbf{r}_{b a} \\ \mathbf{r}_{b g} \end{array}\right]=\left[\begin{array}{c} \mathbf{q}_{w b_{i}}^{*}\left(\mathbf{p}_{w b_{j}}-\mathbf{p}_{w b_{i}}-\mathbf{v}_{i}^{w} \Delta t+\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}\right)-\boldsymbol{\alpha}_{b_{i} b_{j}} \\ 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \\ \mathbf{q}_{w b_{i}}^{*}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)-\boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{b}_{j}^{a}-\mathbf{b}_{i}^{a} \\ \mathbf{b}_{j}^{g}-\mathbf{b}_{i}^{g} \end{array}\right] \end{equation}\\$

待优化的变量是

$\begin{equation} \left[\begin{array}{lllll} \mathbf{p}_{w b_{i}} & \mathbf{q}_{w b_{i}} & \mathbf{v}_{i}^{w} & \mathbf{b}_{i}^{a} & \mathbf{b}_{i}^{g} \end{array}\right]\\ \left[\begin{array}{lllll} \mathbf{p}_{w b_{j}} & \mathbf{q}_{w b_{j}} & \mathbf{v}_{j}^{w} & \mathbf{b}_{j}^{a} & \mathbf{b}_{j}^{g} \end{array}\right] \end{equation}\\$

但在实际使用中，往往都是使用扰动量，因此实际是对以下变量求雅可比

$\begin{equation} \left[\begin{array}{lllll} \delta \mathbf{p}_{w b_{i}} & \delta \theta_{w b_{i}} & \delta \mathbf{v}_{i}^{w} & \delta \mathbf{b}_{i}^{a} & \delta \mathbf{b}_{i}^{g} \end{array}\right] \end{equation}\\$

$\begin{equation} \left[\begin{array}{lllll} \delta \mathbf{p}_{w b_{j}} & \delta \theta_{w b_{j}} & \delta \mathbf{v}_{j}^{w} & \delta \mathbf{b}_{j}^{a} & \delta \mathbf{b}_{j}^{g} \end{array}\right] \end{equation}\\$

3. 残差雅可比的推导

此处只对几个比较复杂的雅可比进行推导（放在附录A中），其余比较简单，感兴趣的可自行完成。

4. 预积分方差计算

4.1 核心思路

在融合时，需要给不同信息设置权重，而权重由方差得来，因此对于IMU积分，也要计算其方差。方差的计算形式与第四章相同，即

$\begin{equation} \boldsymbol{P}_{i, k+1}=\mathbf{F}_{k} \boldsymbol{P}_{i, k} \mathbf{F}_{k}^{\top}+\mathbf{B}_{k} \boldsymbol{Q} \mathbf{B}_{k}^{\top} \end{equation}\\$

但需注意的是，此处

$\begin{equation} \boldsymbol{F}_{k} \end{equation}$ 和

$\begin{equation} \boldsymbol{G}_{k} \end{equation}$ 是离散时间下的状态传递方程中的矩阵，而我们一般是在连续时间下推导微分方程，再用它计算离散时间下的传递方程。

4.2 连续时间下的微分方程

连续时间下的微分方程一般写为如下形式

$\begin{equation} \dot{\boldsymbol{x}}=\boldsymbol{F}_{t} \boldsymbol{x}+\boldsymbol{B}_{t} \boldsymbol{w} \end{equation}\\$

$\begin{equation} \boldsymbol{x}=\left[\begin{array}{l} \delta \boldsymbol{\alpha}_{l}^{b_{k}} \\ \delta \boldsymbol{\theta}_{t}^{b_{k}} \\ \delta \boldsymbol{\beta}_{t}^{b_{k}} \\ \delta \boldsymbol{b}_{\boldsymbol{a}_{t}} \\ \delta \boldsymbol{b}_{\boldsymbol{w}_{t}} \end{array}\right] \end{equation}\\$

$\begin{equation} \boldsymbol{w}=\left[\begin{array}{c} \boldsymbol{n}_{a} \\ \boldsymbol{n}_{w} \\ \boldsymbol{n}_{b_{a}} \\ \boldsymbol{n}_{b_{w}} \end{array}\right] \end{equation}\\$

以上变量排列顺序是为了与lio/vio等常见系统顺序保持一致，所以和之前推导kalman滤波模型的状态方程时会有些不一样。

4.2 连续时间下的微分方程

推导方法已经在之前的文章中介绍过，此处直接给出结果

1）

$\begin{equation} \delta \dot{\boldsymbol{\theta}}_{t}^{b_{k}} \end{equation}$ 的微分方程

$\begin{equation} \delta \dot{\boldsymbol{\theta}}_{t}^{b_{k}}=-\left[\boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}_{t}^{b_{k}}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \end{equation}\\$

$\begin{equation} \delta \dot{\boldsymbol{\beta}}_{t}^{b_{k}} \end{equation}$ 的微分方程

$\begin{equation} \delta \dot{\boldsymbol{\beta}}_{t}^{b_{k}}=-\boldsymbol{R}_{t}\left[\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right]_{\times} \delta \boldsymbol{\theta}_{t}^{b_{k}}+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \end{equation}\\$

$\begin{equation} \delta \dot{\boldsymbol{\alpha}}_{t}^{b_{k}} \end{equation}$ 的微分方程

$\begin{equation} \delta \dot{\boldsymbol{\alpha}}_{t}^{b_{k}}=\delta \boldsymbol{\beta}_{t}^{b_{k}} \end{equation}\\$

4.3 离散时间下的传递方程

得到连续时间微分方程以后，就可以计算离散时间的递推方程了，表示为

$\begin{equation} \boldsymbol{x}_{k+1}=\boldsymbol{F}_{k} \boldsymbol{x}_{k}+\boldsymbol{B}_{k} \boldsymbol{w}_{k} \end{equation}\\$

其中

$\begin{equation} \boldsymbol{x}_{k+1}=\left[\begin{array}{l} \delta \boldsymbol{\alpha}_{k+1} \\ \delta \boldsymbol{\theta}_{k+1} \\ \delta \boldsymbol{\beta}_{k+1} \\ \delta \boldsymbol{b}_{a_{k+1}} \\ \delta \boldsymbol{b}_{\omega_{k+1}} \end{array}\right] \end{equation}\\$

$\begin{equation} \boldsymbol{x}_{k}=\left[\begin{array}{l} \delta \boldsymbol{\alpha}_{k} \\ \delta \boldsymbol{\theta}_{k} \\ \delta \boldsymbol{\beta}_{k} \\ \delta \boldsymbol{b}_{a_{k}} \\ \delta \boldsymbol{b}_{\omega_{k}} \end{array}\right] \end{equation}\\$

$\begin{equation} \boldsymbol{w}_{k}=\left[\begin{array}{c} \boldsymbol{n}_{a_{k}} \\ \boldsymbol{n}_{w_{k}} \\ \boldsymbol{n}_{a_{k+1}} \\ \boldsymbol{n}_{w_{k+1}} \\ \boldsymbol{n}_{b_{a}} \\ \boldsymbol{n}_{b_{w}} \end{array}\right] \end{equation}\\$

由于推导较为复杂，此处给出结论（如下公式），推导过程放在附录B中。

$\mathbf{F}_{k}=\left[\begin{array}{ccccc} \mathbf{I} & \mathbf{f}_{12} & \mathbf{I} \delta t & -\frac{1}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta t^{2} & \mathbf{f}_{15} \\ \mathbf{0} & \mathbf{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t & \mathbf{0} & \mathbf{0} & -\mathbf{I} \delta t \\ \mathbf{0} & \mathbf{f}_{32} & \mathbf{I} & -\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta t & \mathbf{f}_{35} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \end{array}\right]\\$

$\mathbf{B}_{k}=\left[\begin{array}{cccccc} \frac{1}{4} \boldsymbol{R}_{k} \delta t^{2} & \mathbf{g}_{12} & \frac{1}{4} \boldsymbol{R}_{k+1} \delta t^{2} & \mathbf{g}_{14} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \mathbf{0} \\ \frac{1}{2} \boldsymbol{R}_{k} \delta t & \mathbf{g}_{32} & \frac{1}{2} \boldsymbol{R}_{k+1} \delta t & \mathbf{g}_{34} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t \end{array}\right]\\$

其中

$\begin{array}{l} \boldsymbol{f}_{12}=-\frac{\delta t^{2}}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ \boldsymbol{f}_{15}=\frac{\delta t^{3}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ \boldsymbol{f}_{32}=-\frac{\delta t}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ \boldsymbol{f}_{35}=\frac{\delta t^{2}}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ \boldsymbol{g}_{12}=-\frac{\delta^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ \boldsymbol{g}_{14}=-\frac{\delta^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ \boldsymbol{g}_{32}=-\frac{\delta^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ \boldsymbol{g}_{34}=-\frac{\delta^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \end{array}\\$

5. 预积分更新

回到前面遗留的问题，即bias变化时，预积分结果怎样重新计算的问题，现在是时候来解决它了。再次给出它的泰勒展开形式

$\begin{array}{c} \boldsymbol{\alpha}_{b_{i} b_{j}}=\overline{\boldsymbol{\alpha}}_{b_{i} b_{j}}+\mathbf{J}_{b_{i}^{a}}^{\alpha} \delta \mathbf{b}_{i}^{a}+\mathbf{J}_{b_{i}^{g}}^{\alpha} \delta \mathbf{b}_{i}^{g} \\ \boldsymbol{\beta}_{b_{i} b_{j}}=\overline{\boldsymbol{\beta}}_{b_{i} b_{j}}+\mathbf{J}_{b_{i}^{a}}^{\beta} \delta \mathbf{b}_{i}^{a}+\mathbf{J}_{b_{i}^{g}}^{\beta} \delta \mathbf{b}_{i}^{g} \\ \mathbf{q}_{b_{i} b_{j}}=\overline{\mathbf{q}}_{b_{i} b_{j}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_{i}^{g}}^{q} \delta \mathbf{b}_{i}^{g} \end{array}\right] \end{array}\\$

这里，雅可比没有明确的闭式解，但是在推导方差的更新时，我们得到了

$\boldsymbol{x}_{k+1}=\boldsymbol{F}_{k} \boldsymbol{x}_{k}+\boldsymbol{B}_{k} \boldsymbol{w}_{k}\\$

通过该递推形式，可以知道

$\mathbf{J}_{k+1}=\mathbf{F}_{k} \mathbf{J}_{k}\\$

即预积分结果的雅可比，可以通过这种迭代方式计算。

$\boldsymbol{J}_{j}$ 中关于bias的项，就是预积分泰勒展开时，各bias对应的雅可比。

五、总结

可以看出，预积分的推导非常复杂，但只要耐心下来，把思路捋清楚，还是比较容易弄懂的，就是太费纸了。

==============附录A================

附录A 残差雅可比推导

1. 姿态残差的雅可比

1)对i时刻姿态误差的雅可比

$\begin{equation} \begin{aligned} \frac{\partial \mathbf{r}_{q}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} &=\frac{\partial 2\left[\mathbf{q}_{b_{j} b_{i}} \otimes\left(\mathbf{q}_{b_{i} w} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}} \end{array}\right]\right)^{*} \otimes \mathbf{q}_{w b_{j}}\right]_{x y z}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial-2\left[\left(\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}} \end{array}\right]\right)^{*} \otimes \mathbf{q}_{w b_{j}}\right)^{*}\right]_{x y z}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial-2\left[\mathbf{q}_{w b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}} \end{array}\right]\right) \otimes \mathbf{q}_{b_{i} b_{j}}\right]_{x y z}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \end{aligned} \end{equation}\\$

上式可以化简为

$\begin{equation} \begin{aligned} \frac{\partial \mathbf{r}_{q}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}}=-2[\mathbf{0}&\mathbf{I}] \frac{\partial \mathbf{q}_{w b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}} \end{array}\right]\right) \otimes \mathbf{q}_{b_{i} b_{j}}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ =-2[\mathbf{0} & \mathbf{I}] \frac{\partial\left[\mathbf{q}_{w b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}}\right]_{L}\left[\mathbf{q}_{b_{i} b_{j}}\right]_{R}\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}} \end{array}\right]}{\partial \delta \boldsymbol{\theta}_{b_{b} b_{i}^{\prime}}} \\ &=-2\left[\begin{array}{ll} \mathbf{0} & \mathbf{I} \end{array}\right]\left[\mathbf{q}_{w b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}}\right]_{L}\left[\mathbf{q}_{b_{i} b_{j}}\right]_{R}\left[\begin{array}{c} \mathbf{0} \\ \frac{1}{2} \mathbf{I} \end{array}\right] \end{aligned} \end{equation}\\$

2)对j时刻姿态误差的雅可比

$\begin{equation} \begin{aligned} \frac{\partial \mathbf{r}_{q}}{\partial \delta \boldsymbol{\theta}_{b_{j} b_{j}^{\prime}}} &=\frac{\partial 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{j} b_{j}^{\prime}} \end{array}\right]\right]_{x y z}}{\partial \delta \boldsymbol{\theta}_{b_{j} b_{j}^{\prime}}} \\ &=\frac{\partial 2\left[\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right]_{L}\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{j} b_{j}^{\prime}} \end{array}\right]\right]_{x y z}}{\partial \delta \boldsymbol{\theta}_{b_{j} b_{j}^{\prime}}} \\ &=2\left[\begin{array}{ll} \mathbf{0} & \mathbf{I} \end{array}\right]\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right]_{L}\left[\begin{array}{c} \mathbf{0} \\ \frac{1}{2} \mathbf{I} \end{array}\right] \end{aligned} \end{equation}\\$

3)对i时刻陀螺仪bias误差的雅可比

$\begin{equation} \begin{aligned} \frac{\partial \mathbf{r}_{q}}{\partial \delta \mathbf{b}_{i}^{g}} &=\frac{\partial 2\left[\left(\mathbf{q}_{b_{i} b_{j}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_{i}^{q} \delta \mathbf{b}_{i}^{g}} \end{array}\right]\right)^{*} \otimes \mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right]_{x y z}}{\partial \delta \mathbf{b}_{i}^{g}} \\ &=\frac{\partial-2\left[\left(\left(\mathbf{q}_{b_{i} b_{j}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_{i}^{q}}^{q} \delta \mathbf{b}_{i}^{g} \end{array}\right]\right)^{*} \otimes \mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)^{*}\right]_{x y z}}{\partial \delta \mathbf{b}_{i}^{g}} \\ &=\frac{\partial-2\left[\mathbf{q}_{w b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}} \otimes\left(\mathbf{q}_{b_{i} b_{j}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_{i}^{g}} \delta \mathbf{b}_{i}^{g} \end{array}\right]\right)\right]_{x y z}}{\partial \delta \mathbf{b}_{i}^{g}} \\ &=-2\left[\begin{array}{ll} \mathbf{0} & \mathbf{I} \end{array}\right]\left[\mathbf{q}_{w b_{j}}^{*} \otimes \mathbf{q}_{w b_{i}} \otimes \mathbf{q}_{b_{i} b_{j}}\right]_{L}\left[\begin{array}{c} \mathbf{0} \\ \frac{1}{2} \mathbf{J}_{b_{i}^{q}}^{q} \end{array}\right] \end{aligned} \end{equation}\\$

2. 速度残差的雅可比

1)对i时刻姿态误差的雅可比

$\begin{equation} \begin{aligned} \frac{\partial \mathbf{r}_{v}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} &=\frac{\partial\left(\mathbf{q}_{w b_{i}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}} \end{array}\right]\right)^{-1}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial\left(\mathbf{R}_{w b_{i}} \exp \left(\left[\delta \boldsymbol{\theta}_{b_{i} b_{i}^{b}}\right]_{\times}\right)\right)^{-1}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial \exp \left(\left[-\delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}\right]_{\times}\right) \mathbf{R}_{b_{i} w}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial\left(\mathbf{I}-\left[\delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}\right]_{\times}\right) \mathbf{R}_{b_{i} w}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\frac{\partial-\left[\delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}\right]_{\times} \mathbf{R}_{b_{i} w}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}} \\ &=\left[\mathbf{R}_{b_{i} w}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)\right]_{\times} \end{aligned} \end{equation}\\$

2)对i时刻速度误差的雅可比

$\begin{equation} \frac{\partial \mathbf{r}_{v}}{\partial \delta \mathbf{v}_{i}^{w}}=-\mathbf{R}_{b_{i} w} \end{equation}\\$

3)对i时刻加速度bias误差的雅可比

$\begin{equation} \frac{\partial \mathbf{r}_{v}}{\partial \delta \mathbf{b}_{i}^{a}}=-\frac{\partial \boldsymbol{\beta}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{a}}=-\mathbf{J}_{b_{i}^{a}}^{\beta} \end{equation}\\$

3.位置残差的雅可比

位置残差的雅可比比较简单，不在这里推了，照猫画虎自己推一下就行。

==============附录B================

附录B 离散时间递推方程推导

1. $\begin{equation} \delta \boldsymbol{\theta}_{k+1} \end{equation}$ 的推导

由于连续时间下有

$\begin{equation} \delta \dot{\boldsymbol{\theta}}=-\left[\boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \end{equation}\\$

则离散时间下应该有

$\begin{equation} \delta \dot{\boldsymbol{\theta}}_{k}=-\left[\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}_{k}+\frac{\boldsymbol{n}_{\omega_{k}}+\boldsymbol{n}_{\omega_{k+1}}}{2}-\delta \boldsymbol{b}_{\omega_{k}} \end{equation}\\$

因此有

$\begin{equation} \delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-\left[\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{k}}\right]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\delta t \frac{\boldsymbol{n}_{\omega_{k}}+\boldsymbol{n}_{\omega_{k+1}}}{2}-\delta t \delta \boldsymbol{b}_{\omega_{k}} \end{equation}\\$

令

$\begin{equation} \bar{\omega}=\frac{\omega_{k}+\omega_{k+1}}{2}-\boldsymbol{b}_{\omega_{k}} \end{equation}\\$

则上式可以重新写为

$\begin{equation} \delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k}}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_{k}} \end{equation}\\$

2. $\begin{equation} \delta \boldsymbol{\beta}_{k+1} \end{equation}$ 的推导

由于连续时间下有

$\begin{equation} \delta \dot{\boldsymbol{\beta}}=-\boldsymbol{R}_{t}\left[\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \end{equation}\\$

则离散时间下应该有

$\begin{equation} \begin{aligned} \delta \dot{\boldsymbol{\beta}}_{k}=&-\frac{1}{2} \boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{\theta}_{k} \\ &-\frac{1}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{\theta}_{k+1} \\ &+\frac{1}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \end{equation}\\$

把前面求得的

$\begin{equation} \delta \boldsymbol{\theta}_{k+1} \end{equation}$ 的表达式代入上式，可得

$\begin{equation} \begin{aligned} \delta \dot{\boldsymbol{\beta}}_{k}=&-\frac{1}{2} \boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{\theta}_{k} \\ &-\frac{1}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left\{\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k}}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_{k}}\right\} \\ &+\frac{1}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \end{equation}\\$

经过一系列合并同类项以后，最终的合并结果为

$\begin{aligned} \delta \dot{\boldsymbol{\beta}}_{k}=&-\frac{1}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right] \times\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{1}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned}\\$

由导数形式可以得到递推形式如下

$\begin{aligned} \delta \boldsymbol{\beta}_{k+1}=& \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{2}}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned}\\$

3. $\delta \boldsymbol{\alpha}_{k+1}$ 的推导

由于连续时间下有 $\delta \dot{\boldsymbol{\alpha}}_{t}=\delta \boldsymbol{\beta}_{t}$ ，则离散时间下应该有

$\begin{aligned} \delta \dot{\boldsymbol{\alpha}}_{k}=& \frac{1}{2} \delta \boldsymbol{\beta}_{k}+\frac{1}{2} \delta \boldsymbol{\beta}_{k+1} \\ =& \delta \boldsymbol{\beta}_{k} \\ & \quad-\frac{\delta t}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{2}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{2}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t}{4} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ & \quad-\frac{\delta t}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned}\\$

由导数形式可以写出递推形式

$\begin{aligned} \delta \boldsymbol{\alpha}_{k+1}=& \delta \boldsymbol{\alpha}_{k} \\ &+\delta t \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t^{2}}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{3}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t^{2}}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned}\\$

多传感器融合定位理论基础（十一）：IMU预积分模型及应用

任乾

一、概述

二、预积分问题引入

三、预积分模型介绍

四、预积分在优化中的使用

1.使用思路

2. 残差设计

3. 残差雅可比的推导

5. 预积分更新

五、总结

==============附录A================

附录A 残差雅可比推导

1. 姿态残差的雅可比

2. 速度残差的雅可比

3.位置残差的雅可比

==============附录B================

附录B 离散时间递推方程推导

1.

的推导

2.

的推导

3.

的推导

为你推荐

优化方法理论合集（3）——拉格朗日问题

PX4代码阅读笔记（四）——commander详解

四足机器人优化方法初探：力分配与QP优化

【Matlab控制系统仿真（2）】系统简单判稳

自抗扰控制理论（十七）使用C++实现LADRC封装类

MATLAB机器人工具箱基础（一）

评论（0）

关于作者

任乾

65

0

6

3

语义SLAM | 深度学习用于特征提取 : GCN-SLAM（一）

语义SLAM | 深度学习用于特征提取 : GCN-SLAM（二）

SVO源码解读(五)：建图—深度滤波器

相关推荐

最优化学习笔记1——关于拟牛顿法推导

现代控制理论线性系统入门(二)状态变量的解和渐近稳定性

OPENGL -- 快速理解坐标转换系统

自抗扰控制理论（五）ADRC控制并级系统

Webots串级机械臂建模仿真过程-详细！

教程 | 阿克曼结构移动机器人的gazebo仿真（八）

热门泡泡

30积分 失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分 想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

忘记密码

修改头像

添加你感兴趣的标签

举报类型（必选）

举报详情（选填）

$\begin{equation} \delta \boldsymbol{\theta}_{k+1} \end{equation}$ 的推导

$\begin{equation} \delta \boldsymbol{\beta}_{k+1} \end{equation}$ 的推导

$\delta \boldsymbol{\alpha}_{k+1}$ 的推导

30积分失眠，聊聊自己搞ROS的心得体会吧

5积分想买能用ROS2的开发套件。或者开发板