0. 简介
利用牛顿定律解决力学问题是我们非常熟悉的内容,首先经由受力分析得到微分方程,知乎之后求解即可,但随着体系逐渐复杂,未知的约束反力逐渐变多,复杂的(二阶)微分方程也逐渐变多,牛顿力学在解决复杂体系时面临了困境,时代呼唤新的方法——分析力学。
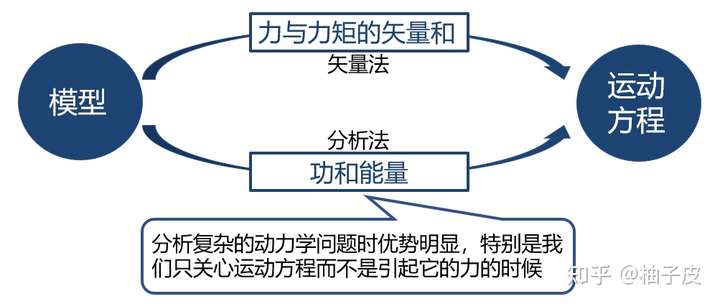
分析法与矢量法(牛顿力学)都是由模型到微分方程的工具,但其处理的物理量截然不同,简单来说,分析法处理的是系统的标量物理量(功和能量),而矢量法则针对系统的矢量物理量(力与力矩)。矢量法简单明了,容易理解,而分析法在处理多体问题时优势明显。
1. 约束及其分类
首先介绍一些基本概念:
力学体系:个相互作用质点的集合;
力学体系的位形:力学系的位置状态;
自由度:描述该系统的坐标的独立变分数;
约束:在力学系中,限制质点自由运动的条件。
约束作为力学广泛存在的重要概念,明确其分类是十分必要的。我们从约束的数学表达式的形式入手来讨论约束的分类。设 为描述系统运动的坐标,
某些约束可以表示成的形式,不含有
项,描述了空间中受路径限制的区域,将其称为几何约束;
某些约束表达式含有项,不能表示成
的形式,限制了系统运动速度,将其称为运动约束;
某些运动约束可以通过直接积分来消掉项,进而变换成几何约束,我们把这种运动约束和所有的几何约束称为完整约束,把不能变换成几何约束的运动约束称为非完整约束;
把表达式中不显含时间的约束称为定常约束,显含时间
的称为非定常约束。
2. 广义坐标
对于如图1-1所示的单摆系统,在笛卡尔坐标系中,运动方程为:
其中 为绳索中的拉力。接下来,我们利用约束
、
,来得到使用一个坐标
的动力学方程,可以看出这两个约束皆为几何约束。
因此
本例中 即为广义坐标,可以看出,它不是笛卡尔坐标的形式。
“广义”是为了将其与笛卡尔坐标区分开,但既为坐标,与笛卡尔坐标类似,广义坐标也是用来描述系统空间构造与运动形式的坐标。广义坐标:能够唯一确定质点系位形的参数。注:不同教材对广义坐标的描述不同,笔者认为,广义坐标的个数最好为描述系统所需的最小坐标数(独立坐标数),但广义坐标的数量可以是任意的,只要能够唯一确定系统的位形即可。广义坐标的导数称为广义速度。
由 个广义坐标表示的
个约束方程可以写成以下微分形式(普法夫形式):
其中,第 个广义坐标用
表示,
描述第
个约束。
接着,我们会面临一个问题:为了给约束归类,我们需要判断约束表达式的积分,如何判断普法夫式能否积分成一般的完整约束的形式?下面我们直接给出结果。
可积的约束方程必须为下面的形式,
其中 为标量,由上式及普法夫式,即有
对
与
求偏导,可得
类似地,对
与
求偏导,可得
若满足上两个式子,则约束便可积分为完整约束。
有了以上的讨论,我们可以用广义坐标来描述约束的分类,总结如下:
完整约束:可积分为形式的约束;
非完整约束:不可积分为形式的约束;
几何约束:可表示为形式的约束;
运动约束:不可表示为形式的约束;
定常约束:约束条件与时间无关,即约束方程不显含时间;
非定常约束:约束条件与时间有关,即约束方程显含时间。
接下来,我们有个十分重要的概念性问题需要解决:描述系统所需要的最小广义坐标数一定等于系统的自由度吗?要解决这个问题,我们需要对完整约束与非完整约束进行进一步的讨论。
已知自由度为独立的坐标变分数,最小广义坐标数为描述系统所需要的独立坐标数,约束的普法夫式为
写成变分形式,由于变分与时间间隔 无关,则取
:
不妨令 ,则利用上式表示出的线性相关性,可以消去
,即有
也就是说,约束的存在消去了一个变分
,使得系统的独立变分数降低了。
若约束是完整约束,根据可积分性质,有
在 的情况下,我们可以用
来消去其中的
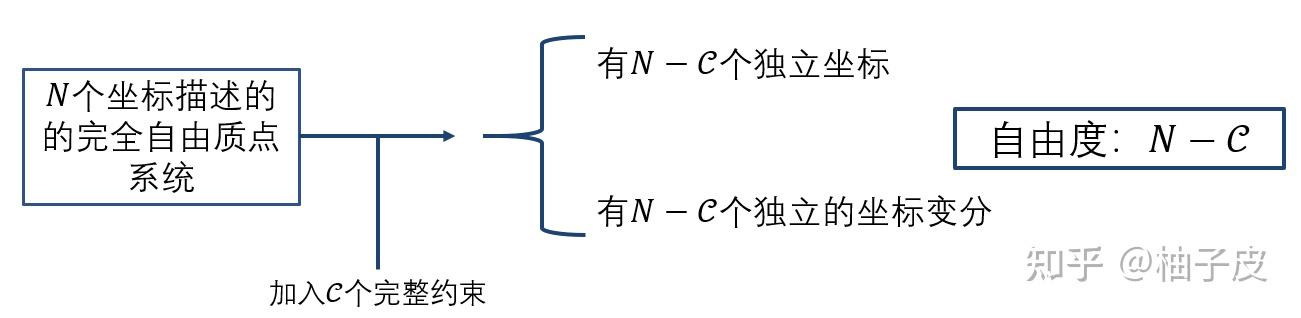
,也就是说,对于完整约束,
与
同时可消,也就是独立坐标数=独立的坐标变分数,如图1-2所示。对于完整系统,独立坐标数(最小广义坐标数)=独立变分数(自由度)。
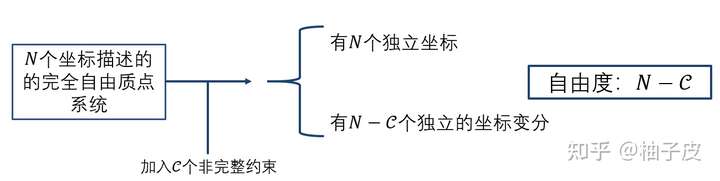
考虑非完整约束时,其无法积分为 的形式,也就是说,它不能像完整约束那样减少系统的独立广义坐标数,如图1-3所示。对于非完整系统,独立坐标数(最小广义坐标数)
独立变分数(自由度),最小广义坐标数要大于自由度。
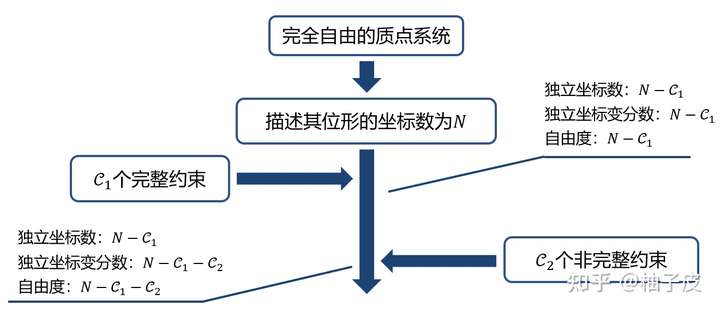
上述可由图1-4说明。
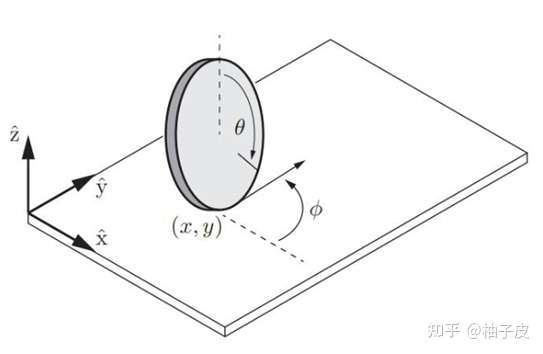
例如一个在平面内纯滚动的轮子,轮心的速度限定在与轮面平行的方向,如图1-5所示。描述轮子的位形需要四个坐标:轮心在平面上的坐标投影 、
,轮子的转角
,轮子的前进方向
,但该轮子只有两个自由度,
是独立的,
、
、
中只有一个是独立的,因为约束
与
的存在。想象我们在驾驶一辆没有方向盘的汽车,四个轮子固定沿直线行驶,我们只能决定车辆的初始朝向以及汽车在我们行驶直线上的位置这两个自由度。
基于以上分析,笔者总结了面对待分析系统时需要的准备工作
面对一个系统,需要先定义描述其位形所需要的广义坐标。这里我们定义的广义坐标只要能够描述系统位形即可,只要写出相关约束,没有其它要求,用它来判断出约束的类型与自由度。
写出广义坐标所对应的约束。在我们随意定义广义坐标时,一定注意不要漏写约束,否则会导致后续计算的全盘错误,这一定程度上也要求我们妥善选取广义坐标。
判断约束的类型,确定系统独立坐标数与自由度。约束的类型至关重要,因为约束的种类直接决定了独立坐标数与独立坐标变分数的关系,这将直接影响到我们如何进行后续的动力学计算,我们将在第2部分认识到这一点。
利用广义坐标去进行动力学计算。
用一个例子来说明本节内容。
例1-1:我们用长度为 的轻杆连接两个质量为
的质点来模拟溜冰鞋的运动,如图1-6所示,溜冰鞋在冰面上滑动,使得质心
只能在与路径相切的
方向移动;溜冰鞋仅在图示平面内运动,找出其所受的所有约束并分类,并给出系统的自由度数。
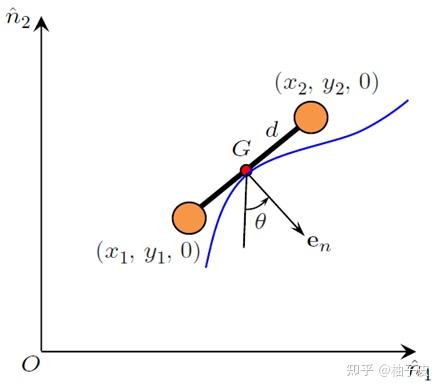
解:两质点在自由运动情况下由坐标 及
描述,系统所受约束为
、
、
以及
,因此该系统有
个自由度。
(随意地)选取广义坐标为 ,注意这里我们选取了比最小广义坐标数要多的广义坐标,约束方程可以表示为
前三个都是完整定常约束,而第四个由于 而
,因此为非完整定常约束。
实际上,由于该系统有三个完整约束,那么描述系统位形所需的独立坐标数(最小广义坐标数)为 个,因此我们可以把广义坐标更改为
去进行后续的动力学计算,
为轻杆与
轴的夹角。注意,虽然需要3个广义坐标才能描述该系统,但该系统的自由度为2。
3. 实位移与虚位移
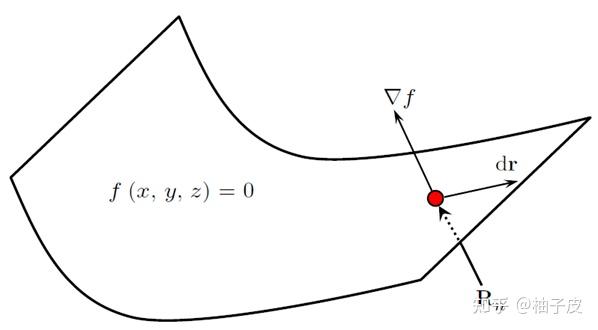
如图1-7所示,考虑一个小球在光滑曲面 上的运动,反作用力
对小球做的功是多少?
曲面方程即小球的约束方程,小球运动满足约束方程,因此对约束方程求导:
表示为
为
的梯度,
为
的位移微元。由于反作用力
也垂直于曲面,因此
与
平行,因此可得
故反作用力(约束力)在实位移微分上做功为0。
若将约束方程变为 ,此时对约束方程求导有
表示为
此时 ,即有
,因此此时反作用力(约束力)在实位移微分上做功不为0。
为了更好的说明前面的讨论,我们考虑下面的情况:
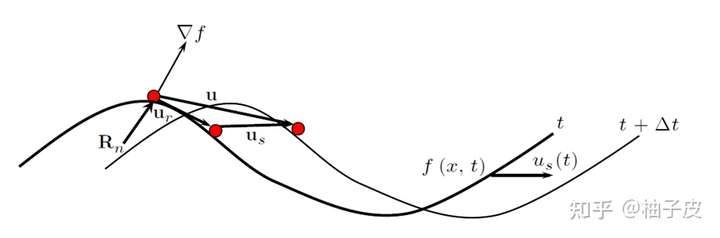
小球沿曲线 做平面运动,同时曲线以速度
做水平运动,图1-8表示出了时间间隔
前后的状态。此时
不与合速度
垂直,即约束力沿位移微元做功不为0。注意到:
,为了消除约束力做功,我们引入虚位移
的概念。
虚位移:质点或质点系在给定瞬时不破坏约束而为约束所许可的任何微小位移,称为质点或质点系的虚位移。
在图1-8中,为了不破坏约束,需要有 ,即虚位移垂直于约束力,平行于相对速度
,故
,这也表示着理想约束的概念:如果作用在一力学体系上诸约束反力在任意虚位移
中所作的虚功之和为零,那么这种约束叫做理想约束。
对于位矢 ,虚位移可以表示为
这个式子表示着虚位移不考虑主动力的作用和初始条件,仅仅满足约束条件;实位移可以表示为
4. 虚功原理
对于一个 个质点的静平衡质点系,我们可以写出牛顿第二定律方程:
其中 为外力,
为约束力;设
为位矢,上式左右两端点乘
得
在理想约束条件下,约束力在虚位移上做功为零,即 ,因此
此即为虚功原理,外力在虚位移上做的功为零。
例1-2. 如图1-9所示系统,试用虚功原理求出使得系统保持静平衡的外力 ,不考虑摩擦,不计连杆质量。
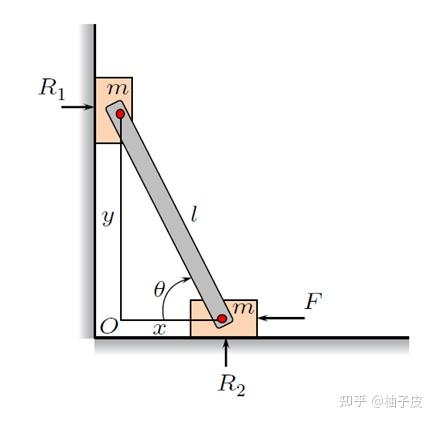
解:约束力在虚位移上不做功,即重力与外力所做的虚功之和为零,因此有:
因 、
,因此
、
,故
5. 达朗贝尔-拉格朗日方程
对于一个 个质点的质点系,我们可以写出牛顿第二定律方程:
其中 为外力,
为约束力;设
为位矢;上式可变形为
具有力的量纲,我们将其称为惯性力,可化“动”为“静”。上式左右两端点乘
得
由虚功原理,在理想约束条件下,约束力在虚位移上做功为零,即有 ,因此
此即为达朗贝尔-拉格朗日方程,外力与惯性力在虚位移上做的功为零。
参考文献:F. Daqaq. Dynamics of particles and rigid bodies: a self-learning approach[M]. Hoboken, NJ: John Wiley & Sons, 2018.







评论(0)
您还未登录,请登录后发表或查看评论