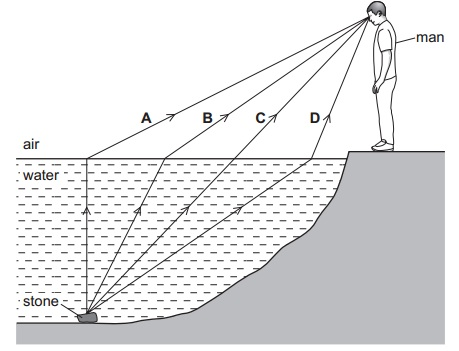
已故著名物理学家张首晟先生有一次在谈及孩子教育问题的时候讲了一个故事:他带一双儿女在海边度假,他问儿子,如果妹妹在海里遇到了危险,由于跑步比游泳快,选择什么路径才能最快到达妹妹身边呢?有3个选项:(参考标题图,假设妹妹在Stone的位置):
- 沿着直线最短的路径 (路径C)
- 在陆地上跑尽量长的距离,因为跑步的速度快于游泳 (路径A)
- 介于A和C之间的折线路径 (路径B)
你猜到答案了吗:路径B!
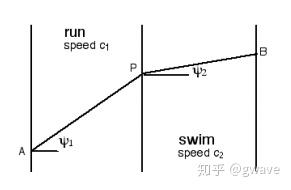
对!这恰恰也是光折射时所走的路径。原来光很“聪明”,它会选择走最快的路径!1662年,皮埃尔·德·费马提出(Pierre de Fermat)费马定理 ,也称最短时间原理( Principle of Least Time)来解释这个现象,但他并没有说明为什么光会选择时间最短的路径。
如果说量子力学和相对论描述的极小和极快世界的规律,颠覆了牛顿经典力学大厦,那么,当时没有人会想到,从这个不起眼的光学折射现象出发,能在牛顿力学如日中天的经典力学领域,还能重建一套更为简洁的新体系!而且,这套思想在量子力学和相对论中仍然有效!在贝叶斯机器学习中,变分推理也是Approximate Inference的一种重要方法。所以,对相关问题进行了一点研究,非物理专业,请轻拍。
自然界类似于上述的最短光程例子还有很多,比如:
- 自由落体为何总是垂直落下,不打个弯呢?自由落体走的也是最快路径!
- 失重状态下的水珠是球形的,在表面积一定时,球型的体积最大;
- 悬链线的重心最低。

宇宙真的很“聪明”?为什么造物主好像这么斤斤计较,总要这么“节约”呢? 早在古希腊时期,亚里士多德就在观察行星运动时,就注意到这种“节约”的特点,他认为天体沿着最短路线最快速的运行;公元前125年,希腊数学家 Hero of Alexandria发现了光的最短路径现象;欧拉更是认为宇宙万物运行的规律都与极值有关。

1696年6月,著名数学家约翰•伯努利(Johann Bernoulli)在欧洲第一份德语科学期刊Acta Eruditorum 中向全世界科学家公开征求「最速降线」(Brachistochrone Curve,源自古希腊语,意为最短时间)问题的解法[1]。「最速降线」问题要找到一个函数,沿着该函数曲线下降的物体能最快达到目标点。伯努利家族是数学豪门,三代出了8位杰出数学家,但随着弟弟数学天才能力的成熟,兄弟两人的关系从合作演变为嫉恨。
约翰•伯努利收到了5位数学家的回复,分别是他哥雅各布•伯努利(Jacob Bernoulli,推导了大数定律第一版和自然常数e的发现者)、牛顿、他的老师莱布尼茨(Gottfried Leibniz)、埃伦弗里德(Ehrenfried Tschirnhaus)和他的学生洛必达侯爵(Guillaume de L'Hôpital)。还记得大一求极限非常好用的洛必达法则吗?约翰做了候爵十年数学老师,洛必达法则是侯爵花了相当于500磅银子的钱从约翰老师那里买来的。不过,侯爵能独立解决最速降线问题,说明数学能力也是很强的,侯爵还编纂了第一本系统阐述微分(没有积分)的教科书呢,他的妻子Marie-Charlotte de Romilley de la Chesnelaye也是一位数学家,原来,数学才是侯爵的真爱!
据说,牛顿在收到信后说:“我不喜欢在数学问题上被外国人戏弄”,熬了一个夜解决了这个问题,并匿名提交了解法。约翰是莱布尼茨的学生,牛顿和莱布尼茨为了微积分的发明权打着官司,这种微妙的关系你懂的。看到了牛顿精彩的解答,约翰•伯努利猜到了答题者的身份,他形容自己「靠着爪印认出了狮子」(recognizes a lion from his claw mark)。
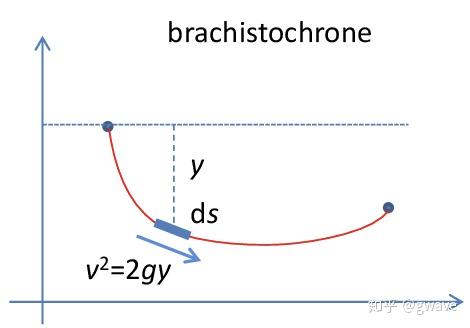
按一般思路,可以通过积分的方法来最速降线的时间,可以通过积分的方法:假设我们考虑上图中的质点运行经过 需要时间
,那么
,
(势能全部转化为动能,化简
) ,
,所以
,A和B分别对应起点和终点。但由于
和
之间的函数关系未知,导致无法进行积分。
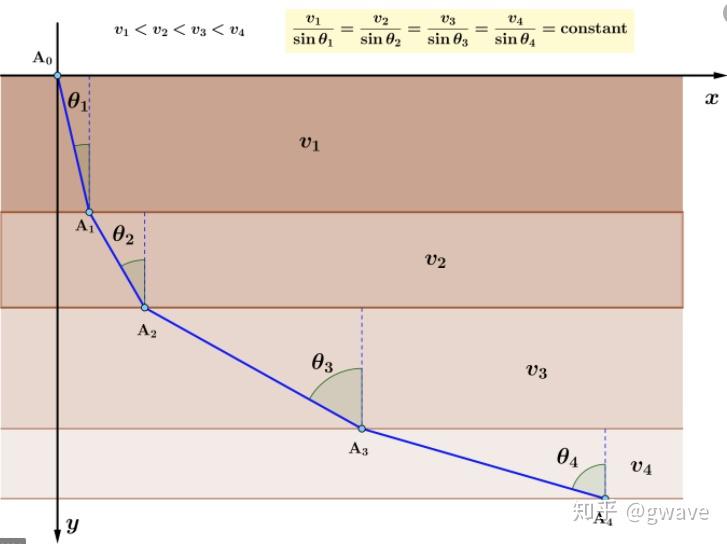
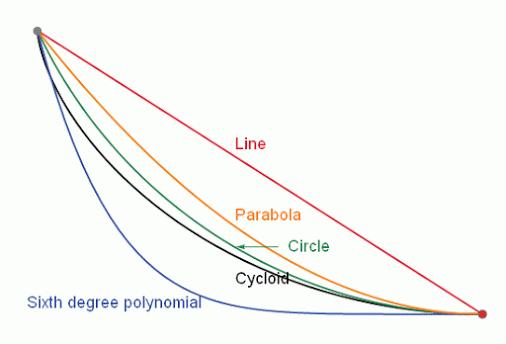
约翰•伯努利提出了一个巧妙的利用费马原理的方法。天才的把最速降线和光走最快路径这两个问题了联系了起来:假设光要经过很多层不同密度的透明物质,每次都会发生折射,也每次都选择最短时间的路径,这样就可以利用费马定理 进行求解,最后他发现最速降线是一条园滚线,也称摆线(cycloid)。
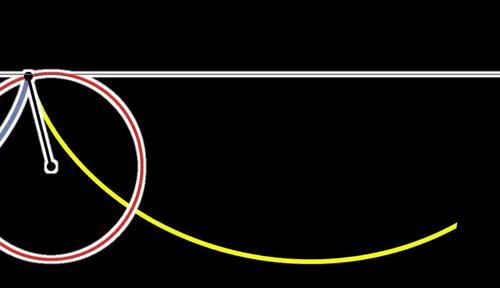
为了超越弟弟的方案,雅各布•伯努利提交了一个难度更大也更具有通用性的解法。之后,约翰•伯努利的学生欧拉(Leonhard Euler)和欧拉的学生拉格朗日(Joseph Lagrange)在雅各布方法的基础上发展出了变分(Calculus of Variation)。拉普拉斯曾说:“读读欧拉吧,他是所有人的老师”,这么算来,约翰•伯努利可以算是所有人的师祖了。
变分法可以系统化地解決「最速降线」这类问题的学问。当时没有人会想到,这门比牛顿力学更牛更抽象的学问成为了拉格朗日力学的基础,被应用于电磁学、相对论甚至非力学领域,与量子场论也密切相关。贝叶斯机器学习也有应用。
话说雅各布•伯努利曾对悬链线问题公开求解,被弟弟约翰成功地解决了,约翰也因此跻身当时欧洲顶尖数学家之列,但却加深了兄弟间竞争和嫌隙。悬链线函数也属于泛函的范畴,悬链线的重心最低。 最小作用量原理(the Principle of Least Action)可解释最快速降、悬链线等物理现象,但如何求解最小作用量呢?
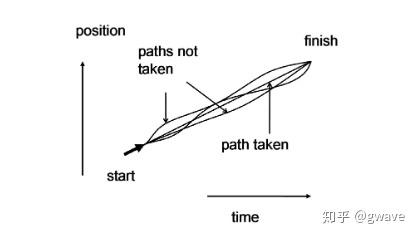
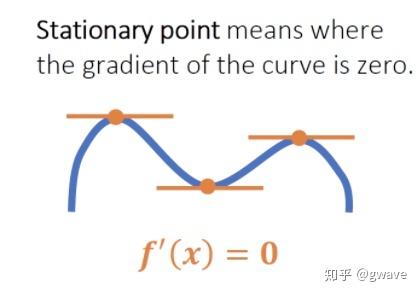
我们知道,求一个函数的极值,可以令其一阶导数等于0,得到驻点(Stationary Point)。驻点虽没有明确说明该点是最大值或最小值,但检查下二阶导数正负性便知。 再深入一步,为啥通过一阶导数等于0来确定最值呢? 因为驻点的一阶导数为0,对 进行稍微变化,
几乎不会变化(二阶及以上的导数所带来的误差小,忽略不计)。Stationary平稳(下图中橙色的线很平:-))要表达的也就是这个意思。这个想法虽然简单,但非常重要,变分的思想也是源于此。
最速降线这类问题都要求最值函数,求最值自然会联想到另一阶导数为0的方法,但问题是:下降曲线的函数都不知道,更不知道要对哪个函数求导。 因此,要寻找一种新的方法:不是找一个能取到最值的点,而是要找一个能取到最值的函数! 重新定义一下问题:在由多个函数组成的候选函数族(Family of functions)中,寻找一个能令泛函达到最值的函数。这也就是泛函(Functional)名称的由来吧,“泛”有“多”的意思。 泛函是函数的函数,输入一个函数,输出一个数值(标量)。 变分法是求泛函(Functional)最值的方法(类似于:驻点是求函数最值的方法)。
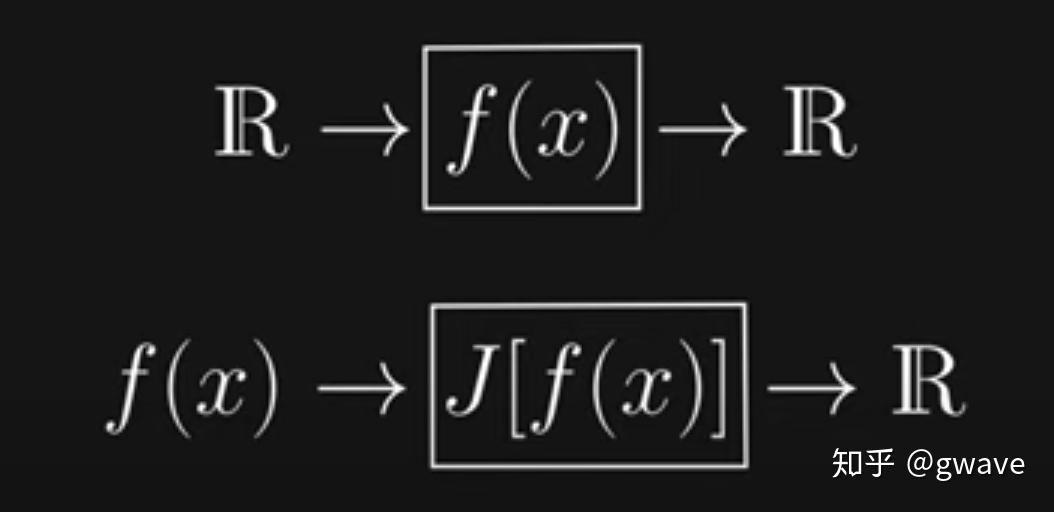
泛函应用广泛,远不限于最速降线问题,在物理学中是拉格朗日力学的基础,在机器学习中也多有应用:
- 熵
可以作为一个典型的泛函例子,对于不同的概率密度函数
,
返回一个标量。寻找最大熵的分布,就是在不同的
中,选择
最大的。注意这里
是一个函数 -- 概率密度函数PDF。
- 变分推断(Variational Inference)[2]
- 深度学习中VAE(Variational Auto Encoding)。
为了更容易理解泛函的核心思想,我们先对比下函数和泛函的特点:
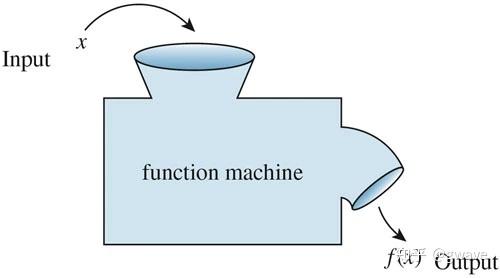
- 可将函数
视为一个机器,输入值
,返回输出值
。
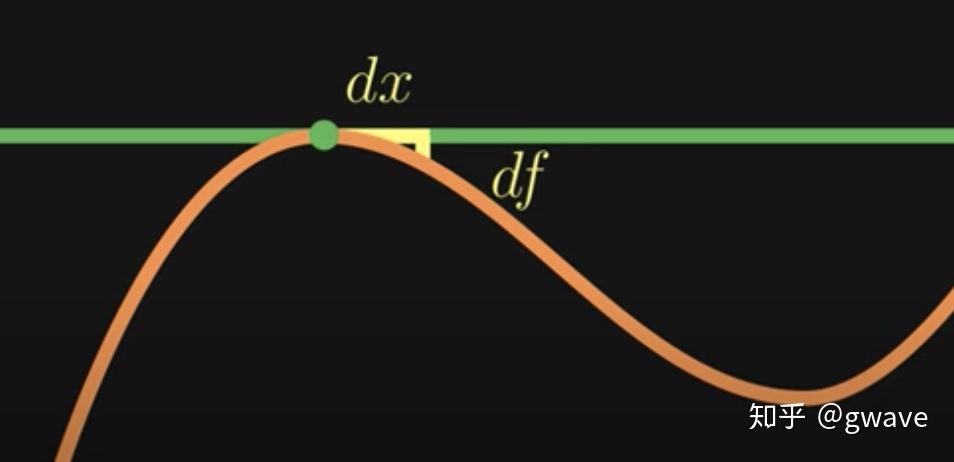
通过令其一阶导数 ,计算出驻点 (Stationary Point),确定极值(可能需要求二阶导数);所谓Stationary(平稳)是指在驻点上,对
增加或减小一个很小的量
,
值保持不变,即
,驻点通常是(局部)最值。
- 可将泛函
视为一个机器,输入函数
,返回一个标量数值
。通过欧拉-拉格朗日方程找到一个函数使泛函取得极值(Extrema),这个函数被成为泛函的平稳函数(Stationary Function of Functional)。可以类比于函数:对稳态函数
施加微小变化,变成
,泛函的返回的值保持不变,即
。
函数和泛函对比:
| 函数 | 泛函 | |
|---|---|---|
| 输入 | 自变量 x | 函数y(x) |
| 输出 | 应变量 y(x),数字(标量) | 泛函 J[y],数字(标量) |
| 最值的形式 | 驻点(Stationary Point) | 平稳函数(Stationary Function) |
| 求最值的方法 | 驻点:dy/dx = 0 | 变分法:欧拉-拉格朗日方程 |
| 微分 | 在自变量x 上加上一个微小的变化量h,当h趋近于0时,所引起y的变化量为0 | 在函数y(x) 上加上一个微小的变化量得到新函数y'(x),J‘[y’]-J[y]=0 |
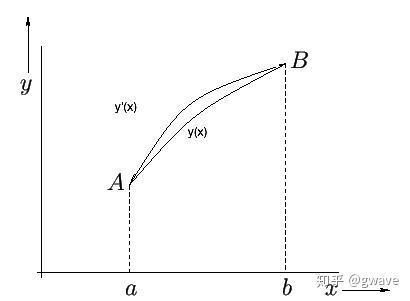
目的: 通过变分法寻找平稳函数 ,使泛函
达到最值(Extrema)。
求解思路:类比于在驻点(一阶导数 )附近施加一个微小扰动,该扰动所引起的
;假设
就是要求的平稳函数(使泛函达到最值Extrema),对
进行微小的扰动,分析力学里称之为“虚位移”,变成
(对应上图中的
),则
应等于0,
,其中
。
这个积分项又是从哪里来的呢?上文提到由于路径函数未知,而无法进行积分的问题。我们知道:泛函 的自变量是
,既然将
作为泛函的输入, 那么把
和
一并输入能包括更全面的信息,于是,雅各布将
定义为一个依赖
的任意函数,并对
在
和
之间进行积分,上面提到的路径函数
可以看成是
的一个例子。通过下一节的欧拉-拉格朗日方程(Euler-Lagrange Equation)的推导,把这个难解的积分求极限问题转变为一个相对容易的微分方程加以解决。
这项工作归功于雅各布•伯努利,他为了压过弟弟的风头,创造出了更通用的解决方法,并经欧拉和拉格朗日的工作发展为变分法。
注意:
- 在临界点A和B,
与
相等,即:
。
- 由于我们关心的变化是由函数
变化所引起的,而非
变化所引起,因此假设
没有变化:
,也称等时变分(
轴是时间轴)。
下一节重点推导欧拉-拉格朗日方程,该方程是变分和拉格朗日力学(Lagrangian Mechanics)的核心,以及从该方程引出汉密尔顿力学,最后对拉格朗日量(Lagrangian)和哈密尔顿量(Hamiltonian)进行对比。
牛顿力学擅长解决一些简单的物理问题,比如只有一个约束条件的单摆(Simple Pendulum)问题。
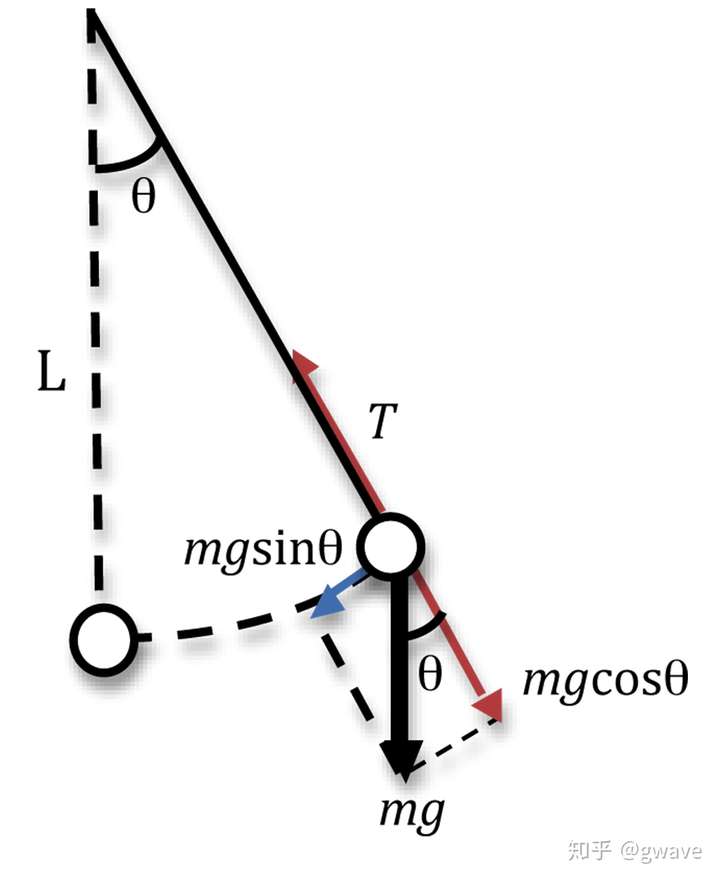
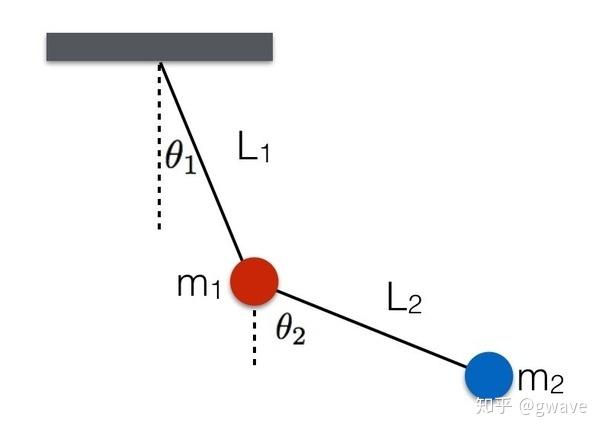
但是对于多约束问题,比如双摆(Double endulum),牛顿力学求解就很复杂。而用分析力学就简明得多,这是由于后者引入了广义坐标,而非牛顿力学的笛卡尔坐标,巧妙的利用约束力做虚功的特点,有效减少了方程数量和问题复杂度。
参考
- ^https://en.wikipedia.org/wiki/Brachistochrone_curve
- ^PRML p.462 Bishop







评论(0)
您还未登录,请登录后发表或查看评论