在前面的章节中我们介绍了三种常见的关节空间轨迹规划方法:多项式插值轨迹规划、线性规划以及带抛物线过渡的轨迹规划。下面,我们将开始介绍笛卡尔空间轨迹规划方法,本篇文章主要介绍直线规划。
一、理论分析
1.什么是笛卡尔空间轨迹规划
三维空间过定点O,作三条互相垂直的数轴,它们都以O为原点且一般具有相同的长度单位。这三条轴分别叫做x轴(横轴)、y轴(纵轴)、z轴(竖轴);统称坐标轴。通常把x轴和y轴配置在水平面上,而z轴则是铅垂线;它们的正方向要符合右手规则,即以右手握住z轴,当右手的四指从正向x轴以π/2角度转向正向y轴时,大拇指的指向就是z轴的正向,这样的三条坐标轴就组成了一个空间直角坐标系,点O叫做坐标原点。这样就构成了一个笛卡尔坐标。
当我们使用关节空间轨迹规划时,末端执行器在空间中一定会经过我们设定好的轨迹点,但在两个轨迹点之间的轨迹形状我们无法确定。
在加工工件、规避障碍等工作场景下,我们必须明确机械臂在起始点与目标点之间的轨迹形状,这时我们必须从笛卡尔空间入手,确定末端执行器在笛卡尔空间中的轨迹函数,即笛卡尔空间轨迹规划。
每个路径点通常由工具坐标系相对于工作台坐标系的期望位姿来确定。使用笛卡尔空间轨迹规划时,形成轨迹的样条函数是描述笛卡尔变量的随时间变化的函数。这些路径可直接根据我们指定的路径点进行规划,这些路径点是由{T}相对于{S}来描述的,无需事先进行逆运动学求解。
值得注意的是,笛卡尔空间轨迹规划计算量很大,因为在运行时必须以实时更新路径的速度求出运动学逆解——即在笛卡尔空间生成路径后,最后一步要通过求解逆运动学来得到对应的关节变量。
2.直线规划
在机械臂作业过程中,我们常希望末端执行器在空间中距离较远的两点间作直线运动,而对应的轨迹规划方法称为直线规划。
首先考虑对位置的插补。当起始点与目标点的坐标已知时,我们可以确定由起始点指向目标点的向量,其模值等于两点在笛卡尔空间中的距离。根据精度要求以及规划效率的要求,确定从直线轨迹上取得n个轨迹点,由起始点指向第i个路径点的向量表示为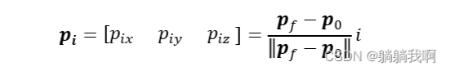
则可得到末端执行器位于第i个轨迹点时的坐标为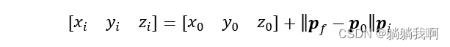
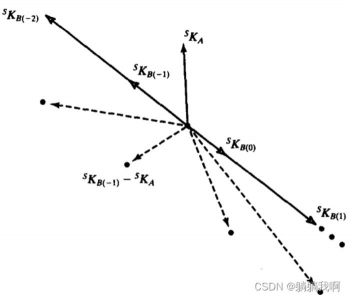
下一步,我们需要考虑对姿态的插补。我们首先将起始姿态到目标姿态的变化看作是由工具坐标系绕一个固定轴旋转得到的。设起始姿态对应旋转矩阵为R0,目标姿态对应旋转矩阵为Rf,则该固定轴可表示为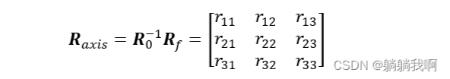
而机械臂末端执行器绕其所旋转角度为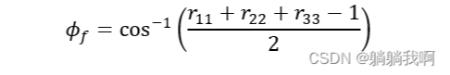
二、程序仿真
使用MATLAB对直线规划进行仿真,路径点个数为50,且选取与前几篇文章中一致的起始点与终止点。
第一步,定义六自由度机械臂的DH参数
%定义关节角度限制
lim1_min = -170 * radian1; lim1_max = 170 * radian1; %关节1(-170,170)
lim2_min = -132 * radian1; lim2_max = 0 * radian1; %关节2(-132,0)
lim3_min = 1 * radian1; lim3_max = 141 * radian1; %关节3(1,141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; %关节4(-165,165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; %关节5(-105,105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; %关节6(-155,155)
%定义关节旋转范围
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;
%D-H参数表
theta1 = 0; d1 = 169.77; a1 = 64.2; alpha1 = -pi/2; offset1 = 0;
theta2 = 0; d2 = 0; a2 = 305; alpha2 = 0; offset2 = 0;
theta3 = 0; d3 = 0; a3 = 0; alpha3 = pi/2; offset3 = pi/2;
theta4 = 0; d4 = -222.63; a4 = 0; alpha4 = -pi/2; offset4 = 0;
theta5 = 0; d5 = 0; a5 = 0; alpha5 = pi/2; offset5 = 0;
theta6 = 0; d6 = -36.25; a6 = 0; alpha6 = 0; offset6 = -pi;
第二步,机械臂运动学建模
L(1) = Link([theta1, d1, a1, alpha1], 'standard');
L(2) = Link([theta2, d2, a2, alpha2], 'standard');
L(3) = Link([theta3, d3, a3, alpha3], 'standard');
L(4) = Link([theta4, d4, a4, alpha4], 'standard');
L(5) = Link([theta5, d5, a5, alpha5], 'standard');
L(6) = Link([theta6, d6, a6, alpha6], 'standard');
%关节偏置
L(3).offset=-pi/2;
L(6).offset=pi;
% 定义关节范围
L(1).qlim=[lim1_min,lim1_max];
L(2).qlim=[lim2_min,lim2_max];
L(3).qlim=[lim3_min,lim3_max];
L(4).qlim=[lim4_min,lim4_max];
L(5).qlim=[lim5_min,lim5_max];
L(6).qlim=[lim6_min,lim6_max];
robot2 = SerialLink(L,'name','AR3');
第三步,定义轨迹的起始点、终止点及步数
T1=transl(-100,-100,300); %起始点齐次变换矩阵
T2=transl(200,-200,400); %终止点齐次变换矩阵
init_ang=robot2.ikine(T1); %运动学逆解
targ_ang=robot2.ikine(T2); %运动学逆解
step = 50; %步数
第四步,直线规划
Tc = ctraj(T1,T2,step); %直线规划,得到每一步的T阵
q=robot2.ikine(Tc); %运动学逆解
figure(f)
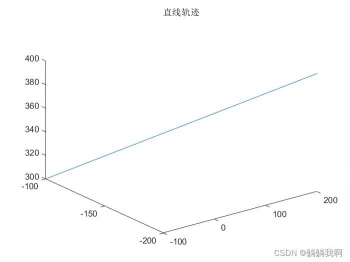
plot3(squeeze(Tc(1,4,:)),squeeze(Tc(2,4,:)),squeeze(Tc(3,4,:)));%输出末端轨迹
title('直线轨迹');
T=robot2.fkine(q); %运动学正解
robot2.plot(q); %动画演示
效果如下所示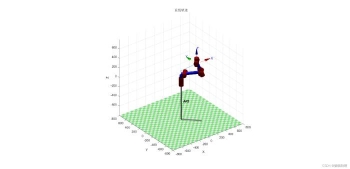
三、编程实现
核心思路就是找到由起始点指向目标点的向量,并在其上求取轨迹点的坐标,进而通过逆运动学求解得到对应的关节变量。
下方为需要用到的两个简单的核心函数
def CalcLinDist(X2,Y2,Z2): #计算目标点到当前点的线段长度
global XcurPos
global YcurPos
global ZcurPos
global LineDist
X1 = XcurPos
Y1 = YcurPos
Z1 = ZcurPos
LineDist = (((X2-X1)**2)+((Y2-Y1)**2)+((Z2-Z1)**2))**.5
return (LineDist)
def CalcLinVect(X2,Y2,Z2):#计算由当前点指向目标点的向量
global XcurPos#当前的
global YcurPos#当前的
global ZcurPos#当前的
global Xv
global Yv
global Zv
X1 = XcurPos
Y1 = YcurPos
Z1 = ZcurPos
Xv = X2-X1
Yv = Y2-Y1
Zv = Z2-Z1
return (Xv,Yv,Zv)








评论(0)
您还未登录,请登录后发表或查看评论